Matematik içinde yaşadığımız evreni tanımlamada inanılmaz derecede başarılıdır. Pek çok matematiksel ilerleme, bu ilerlemelere dayanan fiziksel gelişmelerin kapısını açmıştır. Bunun en güzel örneği, Bernhard Riemann tarafından geliştirilen Riemann geometrisidir. Riemann, fikirlerini ortaya attığında fizik hakkında hiçbir şey düşünmüyordu. Ancak Albert Einstein genel görelilik teorisini Riemann geometrisi olmadan ortaya koyamazdı.

Bu, matematiğin kasıtsız faydasının yalnızca bir örneğidir. Matematikte kullandığımız bir tekniğin fizikçilere yardımcı olduğu ya da fizikteki yeni bir buluşun matematikçilere tamamen yeni matematiksel nesneler veya teoriler yaratmaları için ilham verdiği örnekler çeşitlidir.
Matematiksel düşünceler modern fizikte yol göstermeye devam ediyor ve etmeye de devam edecektir. Bu nedenle de dışarıdan bakan birine fizik ve matematik neredeyse aynı disiplinler gibi görünecektir. Ancak bu noktada da dikkatli olmak önemlidir. Her ne kadar aynı disiplinler gibi gözükseler de birbirlerinden ayrıldıkları noktalar da vardır.
Fizik ve matematik arasındaki en büyük fark nedir?
Bu sorunun cevabını bulmak için bir koşucuyu düşünelim. Eğer ilgili bir soruda gerekli ise, bu koşucunun sol ayağının kaç defa yere çarpacağını hesaplamak mümkündür. Bir matematikçi, koşucunun geçmişte belli bir zaman aralığında, sol ayağını kaç defa yere çarptığını biliyorsa gerekli denklemleri kullanarak gelecekte de kaç defa çarpacağını bulabilir. Hatta bunun için bize birden fazla olası çözüm de verebilir. Ancak hangisinin “doğru” olduğunu söylemez. Ama fizik bunu yapar..
Fizik doğru, fiziksel olarak uygun çözümü bulmanızı sağlarken matematik size yalnızca olası sonuçların bir dizisini verecektir. Basketbol oynarken potaya bir top attığınızda, topun yörüngesini de bildiğinizde, daha sonra ne olacağını belirlemek için topun hareketini tanımlayan denklemleri yazabilirsiniz. Sonrasında da aynı denklemi kullanarak farklı atışlar için de hesaplamalar yapabilirsiniz. Ancak bu denklemler çoğu durumda size iki olası çözüm verecektir.
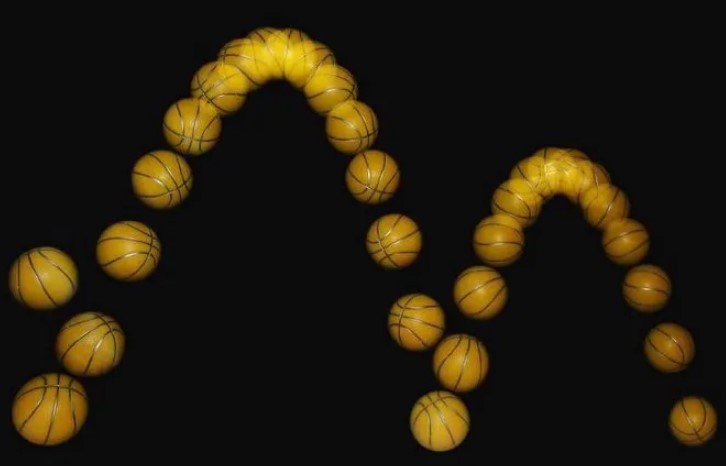
Bu çözümlerden biri aslında aradığınız çözüme karşılık gelir. Ama çoğu durumda elinizde negatif zamana karşılık gelen başka bir çözüm daha olacaktır. Matematiksel açıdan her iki çözüm de doğrudur. Ancak bu çözümlerden yalnızca biri fiziksel olarak geçerlidir. Bu matematikte bir eksiklik değil; fiziğin ve genel olarak bilimin bir özelliğidir. Matematik size hangi sonuçların mümkün olduğunu söyler; fizik (ve genel olarak bilim), ele almaya çalıştığınız spesifik problemle hangi sonucun alakalı olduğunu (veya geçmişte olduğunu veya olacağını) belirlemek için kullandığınız şeydir.
Matematik Fizikçilere Bazı Olasılıklar Sunacaktır
Bazı sistemler doğası gereği kaotiktir. Bu nedenle kimi durumlarda bir sistemin başlangıç koşullarındaki çok küçük, neredeyse ölçülemez farklılıklar, çok farklı potansiyel sonuçlara yol açar. Bazı sistemler de doğası gereği belirsizdir ki bu, kuantum mekaniğinin en mantığa aykırı yönlerinden biridir. Bazen, sisteminizin kuantum durumunu kelimenin tam anlamıyla belirlemek için bir ölçüm yapma eylemi, sistemin kendisinin durumunu değiştirmeyle sonuçlanır.
Tüm bu durumlarda matematik, olasılıkları önceden belirlenebilen ve hesaplanabilen bir dizi olası sonuç sunar. Ancak ölçümü gerçekleştirerek gerçekte hangisinin meydana geldiğini gerçekten belirleyebilirsiniz. Şimdi bir soru soralım. 4’ün karekökü nedir?

Muhtemelen aklınıza hemen 2 geldi. Ancak mümkün olan tek cevap bu değil. Sonucunda cevap “-2” de olabilirdi. Şimdi “16’nın dördüncü dereceden kökü nedir?” diye soralım. Bu durumda elimizde dört doğru cevap vardır. Bunlar 2, -2, 2i ve -2i biçimindedir. Bu sayıların her birini dört defa kendisi ile çarparsanız 16 elde edersiniz.
Yukarıda bulduğumuz tüm cevaplar matematiksel olarak doğru olsa da fiziksel bir sorun bağlamında, bu pek çok olası çözümden içinde yaşadığımız gerçekliği yansıtan yalnızca bir tanesi olacaktır. Hangisinin doğru olduğunu belirlemenin tek yolu ya dışarı çıkıp gerçekliği ölçmek ve fiziksel olarak uygun çözümü seçmektir. Bilim yapma sürecinin doğasında olan bu yaklaşım, içinde yaşadığımız gerçekliğe giderek daha iyi yaklaşımlar yapmamıza yardımcı olur.
Sonuç Olarak
Fizik ve matematik arasındaki ilişki her iki konunun başlangıcına kadar uzanır. Ancak zaman içinde alanlar daha da kapsamlı hale geldikçe ortaya karmaşık bir doku çıkmıştır. Yazımızı Nobel Fizik ödülü sahibi Eugene Wigner (1902-1995) tarafından 1960 yılında kaleme alınan bir cümle ile bitirelim.
“Fizik yasalarının formüle edilmesinde matematik dilinin gösterdiği mucizevi uyum, bizim ne anlayabileceğimiz, ne de hak ettiğimiz bir lütuftur. Bunun kıymetini bilmeli ve geçerliliğini gelecekte de koruması ve diğer bilim dallarına yayılarak bizi şaşırtmaya devam etmesi için dua etmeliyiz.”
Kaynaklar ve ileri okumalar için:
- The unreasonable relationship between mathematics and physics; yayınlanma tarihi: 3 Nisan 2018; Bağlantı: https://plus.maths.org/
- The coevolution of physics and math; Yayınlanma tarihi: 24 Nisan 2018; Bağlantı: https://www.symmetrymagazine.org/
- The biggest difference between physics and mathematics. Yayınlanma tarihi: 30 Ağustos 2022. Bağlantı: https://bigthink.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel








