Günümüzde labirentleri yalnızca dekoratif unsurlar olarak görsek de, tarih boyunca birçok kültür onlara derin anlamlar atfetmiş ve efsanelerine dokumuştur. Labirent tasarlamak ya da bir labirentten çıkmak bugün bize basit bir oyun gibi gelecektir. Ancak bilgisayar bilimcileri ve matematikçiler, labirent üretme algoritmalarının ardındaki karmaşıklığa hâlâ büyük bir hayranlık duymaktadır.

Labirent çizimlerine, ilk zamanlarda kutsal alanlarda yaygın olarak kullanılıyordu. Zamanla bu mistik semboller birer eğlence aracına dönüştü ve sonunda görkemli malikânelerin arazilerinde yer alan çit labirentleri halini aldı. Bu labirentlerin en ünlü örneklerinden biri, tarihi 17. yüzyılın sonlarına dayanan İngiltere’deki Hampton Court Labirenti’dir.
Labirentler, antik anlatılarda da sıkça karşımıza çıkar. Bunlar arasında en dikkat çekici olanı, aşağıda görselini gördüğünüz Girit Labirenti’dir. Ancak, bu labirentte kullanılan geometrik desen, yalnızca Girit’e özgü değildir; birçok farklı kültürde de benzer motiflere rastlanır. Küçük bir alanda son derece uzun bir yolu barındırabilmesi, bu deseni matematikçiler için de ilgi çekici hale getirir.

Bir Labirent İnşa Edelim
Geleneksel bir Girit Labirenti çizmek için işe temel bir çekirdek tasarımıyla başlamak gerekir. İlk bakışta karmaşık gibi görünse de, bu labirenti oluşturmak aslında oldukça kolaydır. Tek yapmanız gereken, belirli bir düzeni takip ederek eğrilerle noktaları birleştirmektir. Ancak, bu işlemi yaparken labirent yolunun olabildiğince uzun olmasını sağlamak da önemli bir hedeftir. Aşağıdaki adımları dikkatle izlerseniz, bu tasarımı kolayca oluşturabileceğinizi göreceksiniz.

Karmaşık görünse de, bu labirentten çıkmak oldukça basittir. Merkeze giden yol uzun ve dolambaçlı olsa da yalnızca bir giriş ve bir çıkış yolu vardır. Bu yüzden yön seçimleri yapmanız gerekmez. Yapmanız gereken tek şey, yolu takip ederek yürümektir. Ayrıca, başlangıç şeklinizi değiştirerek farklı desenlerde ve uzunluklarda labirentler oluşturmanız da mümkündür. Bu, hem yaratıcı hem de eğlenceli bir deneyim sunar!
Bir Labirentten Çıkmak İçin Kullanabileceğiniz Bir Kaç Metot Mevcuttur
Labirentler, ‘basit bağlantılı’ ve ‘çoklu bağlantılı’ olmak üzere iki ana kategoriye ayrılmaktadır. Az önce çizdiğiniz labirent, basit bağlantılı bir labirenttir. Bu tür labirentlerde, tüm duvarlar ya birbirine ya da labirentin dış sınırına bağlıdır.

Basit bağlantılı bir labirentte, sağ ya da sol elinizi bir duvara koyup, bu elin duvarla temasını kaybetmeden ilerlerseniz, eninde sonunda ya merkeze ya da çıkış noktasına ulaşırsınız. Bu tür labirentleri bir döngü şeklinde uzattığınızı hayal edin; bu durumda bir çıkış noktası mutlaka bulunacaktır.
Bu yöntem, her zaman en kısa yolu garanti etmese de, kaybolmadan bir şekilde labirentten çıkmanızı sağlar. Labirentin duvarları, siz dokunarak ilerlerken sürekli bir sınır oluşturur ve yön duygunuzu kaybetseniz bile doğru yolu bulmanıza olanak tanır.
Duvar Takip Etme Kuralı basit labirentlerde neredeyse her zaman işe yarasa da bazı durumlarda etkisiz kalacaktır. Labirent içinde birbirine bağlı olmayan döngüler varsa, sonsuz bir döngü içinde kalabilirsiniz. Ayrıca, labirentin giriş veya çıkış noktası dış sınırla bağlantılı değilse, yöntem sizi doğru yere götürmez.
Bu tür durumlar, özellikle karmaşık labirentlerde oldukça yaygındır. Bu yüzden, çeşitli labirentten kurtulma algoritmaları geliştirilmiştir. Bu yöntemlerden biri, Trémaux’un Algoritmasıdır ve karmaşık yapılı labirentlerde bile her durumda işe yarayan bir çözümdür.
Trémaux’un Algoritması Nasıl Çalışır?
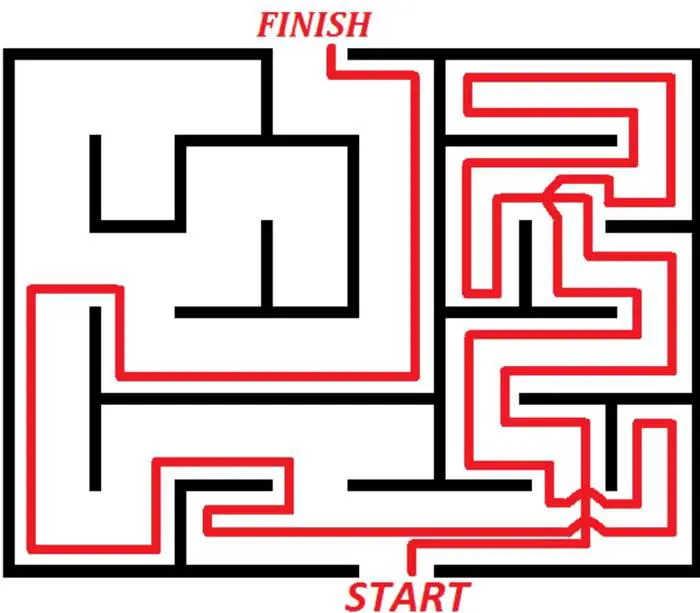
Trémaux algoritması, bir labirentten çıkmak için etkili ve güvenilir bir yöntemdir. Algoritmanın en dikkat çekici yanı, her tür labirentte çalışmasının garantili olmasıdır. Ancak, bu yöntem her zaman en kısa rotayı bulmayı garanti etmez. Yine de, kesin sonuç veren yapısıyla uzun zamandır kullanılan popüler bir tekniktir.
Yeni bir kavşağa ulaştığınızda, rastgele bir yol seçin ve ilerleyin. Bu yolda bir iz (örneğin bir çizgi ya da işaret) bırakın. Eğer bir kavşaktan tekrar geçerseniz:
- Henüz kullanılmamış bir yol varsa, o yolu seçin ve ilerleyin.
- Eğer tüm yollar daha önce kullanılmışsa, bir kez işaretlenmiş olan yoldan geri dönün.
Eğer bir yol iki kez işaretlenmişse, o yola tekrar girmeyin. Bu, çıkmaz yola sapmanızı önler .Bu kuralları izleyerek, en sonunda ya labirentin merkezine ya da çıkış noktasına ulaşacaksınız. Trémaux algoritması, yolların düzenli bir şekilde taranmasını ve çıkmazlara sapmadan labirentin her noktasının keşfedilmesini sağlar.
Pledge Algoritması
Bu algoritma temel olarak engelleri aşmak için tasarlanmış bir yöntemdir. Bununla birlikte, klasik yöntemlerin yetersiz kaldığı durumlarda, bir alternatif olarak kullanılabilir. Algoritma, özellikle labirentte sabit bir referans noktası seçerek yön kaybını önlemeye dayanır.
Algoritmanın başlangıcında, kuzey, güney, doğu veya batı gibi keyfi bir yön belirleyin. Bu yön, algoritma boyunca sizin referans noktanız olacaktır. Örneğin, kuzey yönünü seçtiğinizi varsayalım. Seçtiğiniz referans yönünde ilerleyin ve bir engele çarpıncaya kadar durmadan devam edin.
Engelle karşılaştığınızda, bulunduğunuz yönü not alın ve engel sol tarafta kalacak şekilde dönün. Ardından, sol elinizi duvara koyarak duvarı takip etmeye başlayın. Engeli takip ederken her dönüşünüzü dikkatlice sayın. Dönüşlerin toplamını sürekli olarak takip edin.
Toplam dönüş sıfır olunca yani başlangıçta seçtiğiniz yöne tekrar dönünce ilerlemeye devam edin.
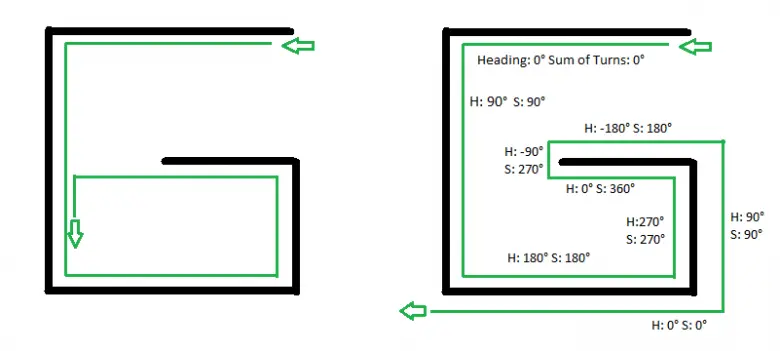
Pledge Algoritması, labirentlerdeki tuzaklara karşı etkili bir çözüm sunar. Ancak, çıkışın ya da merkez noktalarının kesin olarak bulunması için başka algoritmalarla birlikte kullanılması gerekebilir.
Günümüzde bir çoğumuz günlük yaşantımızda bir labirentten kaçma sorunu ile uğraşmasak da bir bilgisayar programcısı için bu tarz algoritmalar ile uğraşmak rutin işlemlerden birisidir.
Kaynaklar ve ileri okumalar
- How to escape a maze – according to maths. Yayınlanma tarihi: 26 Ocak 2017; Kaynak site: Conversation. Bağlantı: How to escape a maze – according to math
- The story of the Minotaur; Yayınlanma tarihi: 1 Mart 2001; Kaynak site: Plus Math. Bağlantı: The story of the Minotaur;/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel