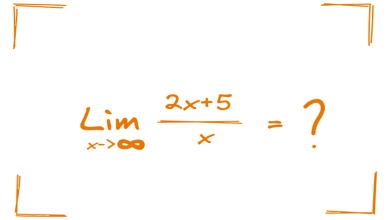Tam sayılar ve bir üçgenin simetrileri arasında nasıl bir ilişki olabilir dersiniz? Modern matematiğin temelini oluşturan grup teorisi, işte böyle tuhaf bir sorunun cevabı olarak ortaya çıktı.

Günümüzden çok çok uzun bir zaman önce matematiğin sayma ihtiyacıyla birlikte ortaya çıktığını hepimiz biliyoruz. Ancak zaman geçtikçe matematik sadece ihtiyaçlarımızdan beslenmekle kalmadı, aynı zamanda merakımızdan da beslenmeye başladı. Böylece gittikçe daha soyut bir uğraş haline gelmeye başladı.
Matematiğin soyutlaşmasındaki ilk büyük adımlardan biri 18. yüzyıl sonlarında atıldı. Bu adım bugün grup teorisi adıyla bildiğimiz ve matematiği hem teorik hem de uygulamalı olarak oldukça değiştiren bir adımdı.
Grup teorisine ismini veren gruplar, tam sayıların temel özelliklerini genelleştirmeyi içerir. Aslında grup teorisinde (az sonra da göreceğimiz gibi) tam sayılara dair çok temel özelliklerle ilgileniriz. Ancak bu temel özellikler bize bambaşka kapılar açar. Bu nedenle grup teorisini mesajları şifrelemekten tutun da virüslerin şekillerini incelemeye kadar birçok alanda kullanırız.
Grup Teorisinin Ortaya Çıkışı ve Grup Teriminin Tanımı
Matematiksel bağlamda grup terimini 1830 yılında o zamanlar henüz 18 yaşında olan Fransız dahi Évariste Galois icat etmişti. Fakat Galois’nın ömrü grup teorisinde yaşanan gelişmeleri görecek kadar uzun olmayacaktı. Çünkü Galois, grup terimini icat ettikten iki yıl sonra bir düelloda hayatını kaybedecekti. Yine de bu kısa ömründe ortaya attığı grup terimi, modern matematiği şekillendirmeye yetecekti.

Peki bir grup tam olarak nasıl bir şeydir? Bir grup en temelde iki matematiksel nesneyi bir işlemle üçüncü bir matematiksel nesne elde edilmesiyle oluşan bir kümeye veya nesneler topluluğudur. Örneğin toplama işlemini düşündüğümüzde tam sayılar bir grup örneğidir. Bir şeye grup diyebilmemiz içinse şu özellikleri sağlaması gerekir:
1. Kapalılık
Bir kümeden aldığımız 2 matematiksel nesneye söz konusu işlemi uyguladığımızda bulduğumuz sonuç yine o kümenin içindeyse küme kapalılık şartını sağlıyor demektir. Mesela toplama işlemi altında tam sayılar kümesini düşündüğümüzde hangi 2 tam sayıyı toplarsak toplayalım yine bir tam sayı elde ederiz. Bu da tam sayılar kümesinin kapalılık şartını sağladığı anlamına gelir.
2. Birleşme
Bir kümeden aldığımız 3 elemana onları nasıl grupladığımız fark etmeksizin söz konusu işlemi uyguladığımızda hep aynı sonucu alıyorsak birleşme şartı sağlanıyor demektir. Örneğin herhangi 3 tam sayıyı [mesela 3+(4+5)=(3+4)+5=12] gruplama şeklimizden bağımsız olarak topladığımızda hep aynı sonucu elde ederiz.
3. Birim Eleman
Bir şeyin grup olabilmesi için grup elemanlarıyla işleme girdiğinde elemanları değiştirmeyen, etkilemeyen bir birim (etkisiz) elemana sahip olması gerekir. Örneğin 0 sayısı toplamanın, 1 ise çarpmanın birim elemanıdır.
4. Ters Eleman
Bir şeyin grup olabilmesi için her grup elemanın bir tersi olmalıdır. Ve grubun herhangi bir elemanı kendi tersiyle işleme girdiğinde birim elemanı vermelidir. Örneğin toplama işlemi altında tam sayılar için her elemanın tersi kendisinin zıt işaretlisidir. Ve bu iki elemanı topladığımızda toplama işleminin birim elemanı olan 0’ı elde ederiz.
Saydığımız bu 4 özellik, bir şeye grup diyebilmemiz için olmazsa olmaz şartlardır. Ancak bir grup, sadece bu 4 özellikten ibaret olmak zorunda değildir.
Abelyen (Değişmeli) Gruplar
Eğer bir grup, yukarıda saydığımız 4 şartla birlikte bir de değişmeli olma özelliğini taşıyorsa bu gruplara abelyen grup veya değişmeli grup denir. Değişmeli olma özelliği isminden de anlaşıldığı üzere grup işlemi gruptan iki elemana sıra fark etmeksizin uygulandığında aynı sonucu vermesidir. Örneğin toplama işlemi altında tam sayıları ele alırsak 3+5 ile 5+3’ün sonucu aynıdır.

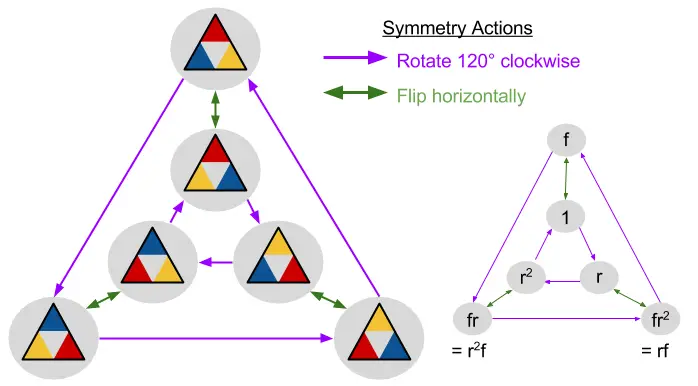
İşe tam sayılar açısından bakınca sanki her grup aynı zamanda bir abelyen grupmuş gibi görünebilir. Ancak bu büyük bir yanılgıdır. Çünkü her grup değişmeli olma şartını sağlayamaz. Bunun için köşeleri 3 farklı renkle etiketlenmiş bir üçgen düşünelim.
Üçgeni 120 derece döndürdüğümüzde veya dikey ekseni boyunca çevirdiğimizde köşelerdeki renkler değişecektir. Geri kalan her şey aynı kalacaktır. İşte üçgenin simetrileri olan ve üçgenin şeklini değiştirmeden bırakan bu dönüşümlerden toplam 6 tane vardır. Bunlar D6 adı verilen bir grup oluşturur. Genel olaraksa D2n , n kenarlı bir düzgün şeklin simetrilerinden oluşan gruplara verilen isimdir. Dolayısıyla D8 de karenin simetrileri grubudur.
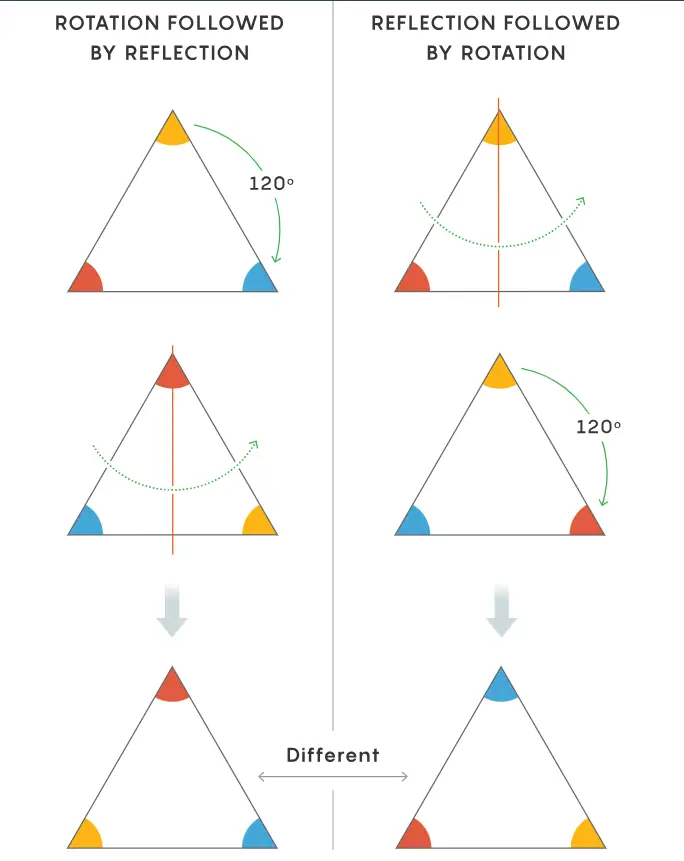
D6 grubunun değişmeli olmadığını görmek oldukça kolaydır. Üçgeni önce yansıtıp sonra döndürdüğümüzde elde ettiğimiz üçgen ile önce döndürüp sonra yansıttığımızda elde ettiğimiz üçgen birbirinin aynısı değildir. Bunu aşağıdaki şekilde daha kolay görebiliriz.
Grup Teorisi Ne İşe Yarar?
Buraya kadar anlattıklarımıza bakınca grup teorisi çok soyut ve uygulamadan uzak görünebilir. Fakat buraya kadar anlattıklarımız sadece grup terimini ve genel olarak grup teorisini tanımlamaktan ibaretti. Grup teorisi kendi içerisinde derya deniz olan bir matematik alanıdır. O halde derya deniz bu teorinin ne gibi uygulama alanları vardır?
Grup teorisinin matematik içerisindeki uygulama alanlarına bakacak olursak harmonik analiz, kombinatorik, cebirsel topoloji, cebirsel sayılar teorisi, cebirsel geometri ve kriptografide grup teorisiyle karşılaşırız.
Matematik dışındaysa simetrilerle ilgili olmasından ötürü fizik ve kimyada birçok yerde grup teorisi kullanılır. Örneğin grup teorisi kuantum mekaniğinde temel parçacıkları sınıflandırmak ve simetrilerini tanımlamak için kullanılır. Veya moleküllerdeki moleküler yapıyı analiz etmek için kimyada grup teorisinden yararlanılır.
Şöyle bir bakınca grup teorisi gerçekten de ilginç ve sıra dışı görünür. Ancak grup teorisi modern matematiği etkilemekle kalmamış aynı zamanda diğer disiplinleri de büyük oranda etkilemiştir.
Kaynaklar ve İleri Okumalar
- ‘Groups’ Underpin Modern Math. Here’s How They Work ; Bağlantı: ‘Groups’ Underpin Modern Math. Here’s How They Work. | Quanta Magazine ; Yayınlanma tarihi: 6 Eylül 2024
- Monster Group (John Conway) – Numberphile ; Video bağlantısı: https://youtu.be/jsSeoGpiWsw?si=HimqKiI-PW_9KaKE
- Grup teorisi, soyutlama ve 196.883 boyutlu canavar – 3Blue1Brown ; Bağlantı: https://youtu.be/mH0oCDa74tE?si=-EZIvpHdcJxqfRrq
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel