Bir zamanlar borsada parasının üçte ikisini kaybeden Isaac Newton’a, bunun olacağını neden önceden göremediği sorulduğunda şu yanıtı vermişti: “Gökcisimlerinin hareketlerini hesaplayabilirim ama insanların deliliğini hesaplayamam.” Yine de, insan davranışlarını ve piyasa dalgalanmalarını hesaplamaya çalışanlar da vardı. Bu isimlerden biri, Fransız matematikçi Louis Bachelier’di.

Modern fiziğin kurucuları olarak kabul edilen Newton ve Leibniz, 17. yüzyılda fiziğe katkı sağlamak amacıyla kalkülüsü geliştirdiler. Bu sürede, aslında var olmayan sonsuz küçük nicelikler kavramını temel alarak ilerlediler. Fransız matematikçi Louis Bachelier ise bu yaklaşımın yalnızca fizikte değil, finans alanında da işe yarayıp yaramayacağını sorguladı. Bugün Bachelier, ekonomide matematiğin sistemli bir biçimde kullanılmasının öncülerinden biri olarak kabul edilmektedir.
Louis Bachelier Kimdir?
Bachelier, 18 yaşına geldiğinde her iki ebeveynini de kaybedince kendini bir anda babasının işlerini yönetirken buldu. Bu sorumluluğu 1891’de askere alınana kadar, yaklaşık iki yıl boyunca sürdürdü. Ancak terhis olduktan sonra hayatında köklü bir değişiklik yapmaya karar verdi. İşleri satıp Paris’e taşınacak, fizik ya da matematik okumaya başlayacaktı. Öte yandan, geçimini sağlamak zorundaydı. Aile şirketinin satışından kalan para bir süre yeterli olsa da, bir iş bulması gerekiyordu.

Sonunda, rakamlara olan hakimiyeti sayesinde Paris Menkul Kıymetler Borsası’nda bir iş buldu. Ancak kısa sürede, içeride tam anlamıyla bir kaos olduğunu fark edecekti. Tüccarlar ve komisyoncular, Palais Brongniart’ın ana salonunda toplanıyor; satın alma ya da satma emirlerini bağırarak ya da el işaretleriyle iletiyordu. Salonda, farklı işlemler için sürekli koşturan onlarca kişi vardı.
Burası, ilk bakışta bir matematikçi için pek uygun bir yer gibi görünmüyordu. Ama artık geri dönüş yoktu. Bachelier, her zaman olasılık teorisine ve rastlantının matematiksel doğasına ilgi duymuştu. Kısa sürede, bazı fikirlerini bu ortamda uygulayabileceğini fark etti. Özellikle dikkatini çeken şey, opsiyon adı verilen sözleşmelerdi.
Opsiyon sözleşmeleri, taraflardan birine belirli bir tarihte, belirli bir fiyattan bir varlığı alma ya da satma hakkı (ama zorunluluğu değil) tanır. Bir varlığı satın alma hakkı veren sözleşmelere alım opsiyonu, satma hakkı verenlere ise satım opsiyonu denir. Eğer fiyatların yükseleceğini düşünüyorsanız alım opsiyonu, düşeceğini öngörüyorsanız satım opsiyonu kullanılır.
Louis Bachelier Rastgeleliği Ekonomiye Dahil Edecekti.
Günümüzde opsiyonları anlamak nispeten kolay; belirli modeller, kurallar ve fiyatlama yöntemleri var. Ancak Louis Bachelier’in zamanında karşılaştığı manzara tam anlamıyla bir kaostu. Bu kaos, özellikle hisse senedi opsiyonlarının fiyatlandırmasında kendini gösteriyordu. Çünkü kimse bu sözleşmelerin neye göre fiyatlanması gerektiğini bilmiyordu.
Yatırımcılar, fiyatın ne olması gerektiği sorusunu matematiksel modellerle değil, pazarlıkla çözmeye çalışıyordu. Herkes kendi tahminine, beklentisine ve pazarlık gücüne göre bir değer öneriyor, bu da piyasalarda öngörülemez bir dalgalanma yaratıyordu.

Bir hisse senedinin fiyatı, alıcılar ve satıcılar arasındaki sürekli çekişmeyle belirlenir. Daha fazla insan bir hisseyi almak isterse fiyat yükselir; satmak isteyenler çoğunluktaysa düşer. Ancak bu dengeyi etkileyen faktörler neredeyse sınırsızdır.
Bachelier, gelecekteki fiyat hareketlerinin geçmiş verilere bakılarak güvenilir biçimde tahmin edilemeyeceğini fark etti. En mantıklı varsayım, herhangi bir anda fiyatın yükselme olasılığıyla düşme olasılığının eşit olduğu ve bu yüzden fiyatların uzun vadede rastgele bir yürüyüş izlediğiydi.
Bu rastgeleliği gösterebilmek için Bachelier, fiziksel bir kavramdan ilham aldı: Brown hareketi. Bu kavram, mikroskop altında gözlemlenen polen parçacıklarının sudaki gelişigüzel hareketini tanımlar. Bachelier, bu düzensiz hareketin doğasını hisse senedi fiyatlarına uyguladı ve fiyatların da benzer biçimde rastlantısal biçimde hareket ettiğini matematiksel olarak göstermeye çalıştı.

Louis Bachelier bu konuyu doktora danışmanı Henri Poincare ile paylaştı. Henri Poincare matematik, astronomi, fizik ve mühendislik de dahil olmak üzere temas ettiği her alana önemli katkılarda bulunmuştu. Tıpkı Bachelier gibi o da yüksek lisans eğitimini Paris Üniversitesi’nde yapmıştı. Ayrıca maden müfettişi olarak akademi dışında da çalışma deneyimi de vardı. Bu nedenle başvuru için doğru kişiydi.
Ancak yine de ekonomi ile matematiği bir arada düşünmek o zaman için alışılmadık bir kavramdı. Ne var ki Poincare, “Spekülasyon Teorisi” başlıklı teziyle 1900 yılında Sorbonne’dan mezun olan öğrencinin çalışmalarını çok da ciddiye almamıştı. Bu tezin ardındaki temel fikir, olasılık teorisinin finansal piyasaları anlamak için kullanılabileceğiydi.
Brown Hareketi Nedir?
Bitkibilimci Robert Brown, mikroskopla incelediği polen taneciklerinin suda düzensiz şekilde hareket ettiğini gözlemledi. Başta bunun canlılıktan kaynaklandığını düşündü, ancak aynı hareketin cansız maddelerde de görüldüğünü fark etti. Bu rastgele kıpırdanışa “Brown hareketi” adı verildi.
Uzun süre açıklanamayan bu olgu, 1905 yılında Albert Einstein’ın Annalen der Physik dergisinde yayımladığı çalışmayla anlam kazandı. Einstein, bu hareketin moleküllerin görünmeyen çarpışmalarından kaynaklandığını ortaya koyarak fiziğe yeni bir bakış kazandırdı.
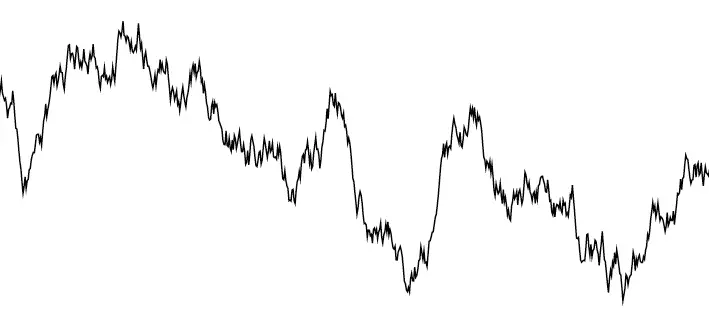
Fizik ve kimya çevrelerinde, Brown hareketini matematiksel olarak açıkladığı için tüm övgü genellikle Einstein’a gider. Oysa Einstein, bu konuda beş yıl gecikmişti. Louis Bachelier, 1900 yılında yazdığı doktora tezinde rastgele yürüyüşlerin matematiğini çoktan tanımlamıştı. Fakat onun ilgilendiği alan fizik değil, hisse senedi fiyatlarının rastgele hareketleriydi.
Ne var ki Bachelier’nin çalışması, zamanının çok ilerisindeydi ve uzun süre görmezden gelindi. Tezi, yazıldıktan ancak 50 yıl sonra, hak ettiği ilgiyi gördü.
Spekülasyon Teorisi Nedir?
Galton kutusu, üzerinde üçgen biçiminde sıralanmış çok sayıda pimin yer aldığı dik bir tahtadır. Üst kısmındaki kaptan bırakılmaya hazır toplar, aşağı doğru düşerken pimlere çarpar. Pimler, topların sağa ya da sola düşme olasılığını eşit kılacak şekilde yerleştirilmiştir. Böylece toplar, aşağı doğru ilerlerken rastgele ama matematiksel olarak öngörülür bir yol izler..

Bununla birlikte, deneyi bir kaç kez tekrar ederseniz aşağı yukarı aynı sonucu göreceğiniz neredeyse kesindir. Matematik yasaları gereği topların çoğu merkezde, az bir kısmı ise kıyılarda toplanacaktır. Merkezden kenara gidildikçe bölmelere giren topların sayısı azalır. Diğer bir deyişle, rastgele toplar eninde sonunda normal bir dağılım oluşturacaktır. ( Detayları bu yazıda inceleyebilirsiniz)

Louis Bachelier, hisse senedi fiyatlarının Galton tahtasındaki toplar gibi rastgele hareket ettiğini düşünüyordu. Ona göre temel soru şuydu: Bir hisse senedi belirli bir fiyattan başlıyorsa ve fiyat hareketleri rastgele ise, belirli bir süre sonra belirli bir değerde olma olasılığı nedir? Bu sorunun matematiksel cevabını, 1900 tarihli tezinde ortaya koymuştu.
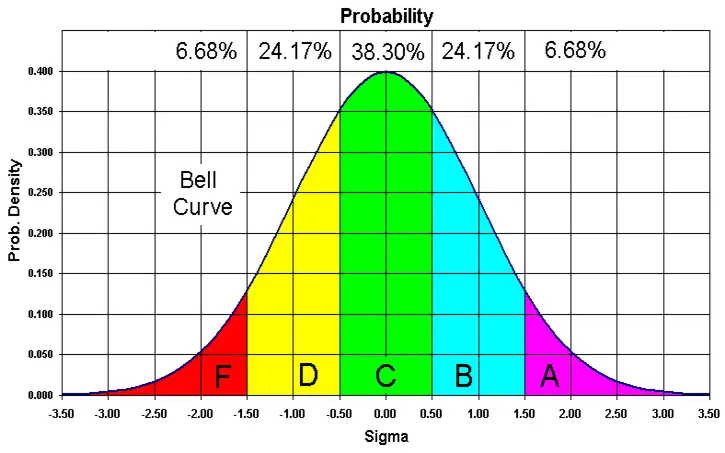
Bachelier, hisse senedi fiyatlarının rastgele bir yürüyüşe geçtiği durumda, zamanla oluşan olasılık dağılımının normal dağılım—ya da daha yaygın bilinen adıyla çan eğrisi—şeklinde olduğunu gösterdi. Varsayımı basitti ama etkiliydi: Herhangi bir anda fiyatın artma olasılığı, azalma olasılığıyla eşitti. Bu temel fikir, modern finans matematiğinin önünü açan önemli bir adımdı.
Bachelier sonunda opsiyonları fiyatlamanın matematiksel bir yolunu bulmuştu. Her bir olası sonucun kar ya da zararını, o sonucun gerçekleşme olasılığıyla çarparak, opsiyonun beklenen getirisini hesapladı. Bu yaklaşım, belirsizlik altındaki değerlemenin temelini oluşturdu.
Bachelier’nin fikirleri, bugün finans dünyasında geniş bir etki alanına sahiptir. Borsada alım-satım stratejilerinden türev ürünlerin fiyatlandırılmasına, risk yönetiminden portföy optimizasyonuna kadar pek çok karmaşık işlem, onun ortaya koyduğu temeller üzerine inşa edilmiştir.
Sonuç olarak
Şansa ve rastlantıya olan hayranlığına rağmen, Louis Bachelier hayatı boyunca yeterince şanslı biri olmadı. Finans dünyasına dair derin ve zamanının ötesinde iç görüler geliştirmiş olsa da, bu katkılar yaşarken hak ettiği ilgiyi görmedi. 1909’dan itibaren Paris Üniversitesi’nde maaş almaksızın ders vermesine izin verildi. Fizik, finans ve matematik alanlarında ufuk açıcı çalışmalar yapmıştı; ancak akademik camiada kalıcı bir saygınlık kazanamadı.
1914 yılında nihayet bir fırsat doğdu. Bachelier için üniversitede kalıcı bir pozisyon açıldı. Fakat aynı dönemde Almanya’nın Fransa’yı işgali başladı. Henüz kimsenin fark etmediği 44 yaşındaki bu matematikçi, askere çağrılarak cepheye gönderildi.

Bachelier, Birinci Dünya Savaşı’ndan sağ çıkmayı başardı. Paris’e döndüğünde, savaşta hayatını kaybeden pek çok genç matematikçi nedeniyle üniversitelerde ciddi açıklar oluşmuştu. 1919 ile 1927 arasında çeşitli üniversitelerde misafir profesör olarak ders verdi. Nihayet 1927 yılında, Besançon Üniversitesi’nde tam zamanlı profesörlük görevine atandı ve 1937’de emekli olana kadar burada kaldı. Ancak bu dönemde dikkat çekici bir araştırma yapmadı. Profesör olduktan sonra, hayatının geri kalanında yalnızca bir makale yayımladı.
Oysa tek başına geliştirdiği fikirler, 1960’lara kadar hisse senedi fiyatlarının rastgele yürüyüş modeli üzerine yapılan çalışmalara yön verdi. Opsiyonlara değer biçerken sezgiye değil, matematiğe dayalı bir yöntem geliştirmeye yönelik ilk girişim ondan gelmişti. Ancak bu alana, Bachelier’den onlarca yıl sonra, 1950’li ve 60’lı yıllarda sadece birkaç kişi ilgi gösterecekti.
Kaynaklar ve ileri okumalar
- Louis Bachelier: An Underappreciated Revolutionary. Yayınlanma tarihi: 8 Mart 2021. Kaynak site: History of data Science. Bağlantı: Louis Bachelier: An Underappreciated Revolutionary
- Courtault, Jean-Michel & Kabanov, Yuri & Bru, Bernard & Crépel, Pierre & Lebon, Isabelle & Marchand, Arnaud. (2000). Louis Bachelier on the Centenary of “Théorie de la Spéculation”. Mathematical Finance. 10. 339-353. 10.1111/1467-9965.00098.
- Johnson, T. The influence of financial practice in developing mathematical probability. Synthese 198 (Suppl 26), 6291–6331 (2021). https://doi.org/10.1007/s11229-020-02636-w
Matematiksel