Matematik, uzun süre boyunca mutlak kesinliğin alanı olarak görüldü. İnsanlar, sorulan her sorunun cevabının bir gün mutlaka matematik içinde bulunabileceğine inanıyordu. Ancak Kurt Gödel, Eksiklik Teoremleri ile bunun bir yanılsama olduğunu gösterdi.

1931 yılında Avusturyalı mantıkçı Kurt Gödel, tarihin en çarpıcı entelektüel başarılarından birine imza attı. O dönemin matematikçileri, tüm matematiksel doğruların üzerine kurulabileceği sağlam bir temel arayışındaydı. Amaç, hem çelişkisiz (tutarlı) hem de eksiksiz olacak bir aksiyomlar sistemi kurmaktı. Böylece tüm matematiksel gerçekler bu temel ilkelerden türetilebilecekti.
Gödel’in yalnızca yirmi beş yaşındayken yayımladığı Eksiklik Teoremleri bu düşünceyi yıktı. Gödel, hangi aksiyomlar kümesi seçilirse seçilsin, bu sistemin kaçınılmaz biçimde eksik kalacağını kanıtladı. Her zaman, o aksiyomlarla kanıtlanamayan ama yine de doğru olan ifadeler var olacaktır.

Bu doğru ifadeleri kanıtlamak için matematikçilerin yeni bir aksiyom eklemesi gerekir. Ancak bu yeni aksiyom listesi de yine doğruluğu kanıtlanamayan başka ifadeler doğuracaktır. Bu durum, matematiksel evrenin, matematikçilerin genellikle “V” olarak adlandırdığı yapının, temelde bilinemeyeceği anlamına gelir.
Gödel’in buluşundan sonraki yıllarda, onun öngördüğü türden çözümsüz sorular gerçekten de ortaya çıktı. Örneğin, sonsuzlukların büyüklükleriyle ilgili süreklilik hipotezi ve bir bilgisayar programının belirli bir girdiyle sonsuza dek çalışıp çalışmayacağını sorgulayan durma problemi karara bağlanamaz sorunlardı.
Kurt Gödel Eksiklik Teoremini Nasıl Kanıtladı?
Gödel’in temel yöntemi, bir aksiyom sistemine ilişkin ifadeleri, sistemin içindeki ifadelere, yani sayılarla ilgili ifadelere dönüştürmekti. Bu eşleştirme, aksiyomlardan oluşan bir sistemin kendisi hakkında tutarlı biçimde konuşabilmesini sağladı.
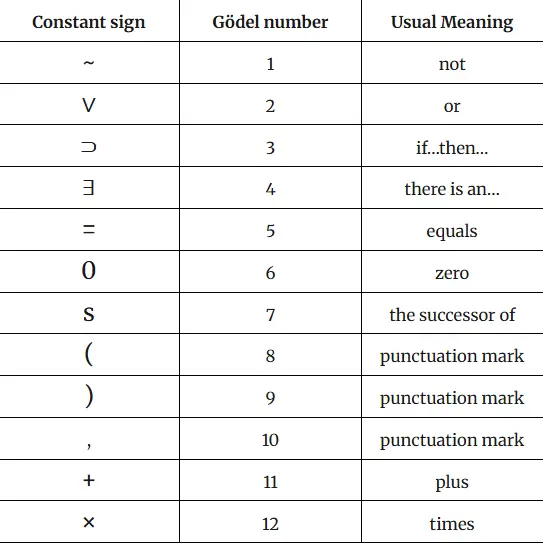
Bu sürecin ilk adımı, herhangi bir matematiksel ifadeyi ya da ifade dizisini, Gödel numarası denen benzersiz bir sayıya karşılık getirmektir. Yukarıda onun düşünme biçimini görebilirsiniz. Bu semboller ve değişkenlerin her türlü birleşimi kendine özgü bir Gödel numarasına sahip olur.
Örneğin 0 = 0 ifadesini ele alalım. Bu formüldeki üç sembol sırasıyla Gödel numaraları 6, 5 ve 6’ya karşılık gelir. Gödel’in bu üç sayılık diziyi tek ve benzersiz bir sayıya dönüştürür. Amacı bu yeni sayının başka hiçbir sembol dizisiyle elde edilememesini sağlamaktır.
Bunun için ilk üç asal sayıyı (2, 3 ve 5) kullanır. Her asal sayıyı, dizideki sembolün Gödel numarası kadar kuvvetle çarpar ve elde ettiği sonuçları birbiriyle çarpar. Sonuçta 0 = 0 ifadesi şu hale gelir: 2⁶ × 3⁵ × 5⁶ = 243.000.000.
Bu eşleştirme yöntemi işe yarar çünkü iki farklı formül hiçbir zaman aynı Gödel numarasını almaz. Gödel numaraları birer tam sayıdır ve her tam sayı yalnızca tek bir şekilde asal çarpanlarına ayrılır. Böylece, bu çarpanlar dizisi, sayının hangi formüle ait olduğunu açıkça gösterir.
Tüm Matematik Gödel Numaraları İle İfade Edilebilir
Gödel bundan sonra bir adım ileri gitti. Matematiksel bir kanıt, bir dizi formülden oluşur. Bu nedenle Gödel, her formül dizisine de ayrı bir Gödel numarası verdi.
Bu yöntemde yine asal sayılar listesini kullanır. Her asal sayıyı, dizide aynı sırada bulunan formülün Gödel numarası kadar kuvvetle çarpar. Örneğin, dizide ilk sırada 0 = 0 formülü varsa, işlem 2²⁴³,⁰⁰⁰,⁰⁰⁰ × … biçiminde başlar. Son olarak, bu değerlerin hepsini çarpar ve formül dizisini temsil eden tek bir sayı elde eder.
Asıl önemli nokta, aritmetik formüllerle ilgili ifadelerin kendilerinin de Gödel numaralarına sahip formüllere dönüştürülebilmesidir. Örneğin şu ifadeyi ele alalım: ~(0 = 0). Bu, “sıfır sıfıra eşit değildir” anlamına gelir.
Bu ifade yanlıştır. Ancak yine de bir Gödel numarasına sahiptir. Tüm formüller için, hatta yanlış olanlar için bile, Gödel numaraları üretebildiğimiz için, bu formüller hakkında onların Gödel numaraları üzerinden konuşabiliriz.
Gödel’in Ek Buluşu Yerine Yazma Yöntemidir
Gödel’in ek buluşu, bir formülün kendi Gödel numarasını o formülün içine yerleştirebileceğini fark etmesiydi. Bu düşünce, oldukça karmaşık sonuçlara yol açtı.
Bunun nedeninin anlamak için (∃x)(x = sy) ifadesini ele alalım. Bu ifade “y değişkeninin bir ardılı vardır” anlamına gelir. Tüm formüller gibi bunun da bir Gödel numarası vardır; bu sayıya m diyelim. Şimdi formüldeki y sembolü yerine m sayısını yerleştirelim. Yeni formül (∃x)(x = sm) biçimini alır ve “m’nin bir ardılı vardır” anlamına gelir.
Şimdi bu yeni formülün Gödel numarasını bulalım. Başlangıçta Gödel numarası m olan bir formülümüz vardı. Bu formülde y sembolü yerine m koyduk ve y sembolünün Gödel numarası 17’dir. Bu nedenle yeni formülün Gödel numarasını sub(m, m, 17) olarak adlandırırız.
Şimdi “Gödel numarası sub(y, y, 17) olan formül kanıtlanamaz.” ifadesini ele alalım. Aynı mantıkla bu ifade de yine tek bir Gödel numarasına sahip bir formüle dönüştürülebilir. Bu yeni formülün de kendine özgü bir Gödel numarası olur; buna n diyelim.
Gödel burada son bir adım daha atar. Önceki formülde geçen her y yerine, bu sefer n sayısını koyar. Böylece yeni bir formül elde eder: “Gödel numarası sub(n, n, 17) olan formül kanıtlanamaz.” Bu yeni formüle G adını verir. G formülü aslında şunu söyler: “Ben kanıtlanamam.”
G formülü kanıtlanabilir mi?
Eğer kanıtlanabilseydi, bu durum G’nin söylediği şeyin tam tersini ifade ederdi. Çünkü G “ben kanıtlanamam” diyor. Tutarlı bir sistemde hem G hem de onun tersi aynı anda doğru olamayacağı için G’nin doğruluğu belirsiz olmalıdır.
Yine de G’nin doğru olduğunu görebiliriz. G, “bu formül kanıtlanamaz” der ve gerçekten de sistemin içinde onu kanıtlayacak hiçbir yol yoktur. Bu yüzden G doğrudur ama sistemin içinde kanıtlanamaz. Bu da sistemin eksik olduğunu gösterir: tüm doğrular kanıtlanamaz.
Peki yeni bir aksiyom ekleyip G’yi kanıtlamak mümkün mü? Gödel bunun da işe yaramayacağını gösterdi. Çünkü yeni aksiyomlarla oluşturulan her sistemde, yine kanıtlanamayan başka bir doğru formül ortaya çıkar.
Sonuçta, matematikte tamamen kapalı ve eksiksiz bir sistem kurmak imkânsızdır. Ne kadar genişletilirse genişletilsin, her zaman kanıtlanamayan bazı doğrular kalır.
Sonuç Olarak
İşte Gödel’in ünlü Eksiklik Teoremi tam olarak bu fikre dayanır. Matematik, kendi içinde bu tür bir ifadeyi ya kanıtlayamaz ya da çelişkiye düşer. Gödel’in bu kanıtı, hem tutarlı hem de eksiksiz bir matematik sistemi kurma hayalini sona erdirdi. Konu ile ilgili 1958 tarihli bir kitaba şu not düşülmüştü. “Eksikliğin anlamı “hâlâ tam olarak kavranabilmiş değildir.” Bu durum bugün de geçerliliğini koruyor.
Kaynaklar ve ileri okumalar
- The foundations of mathematics are unproven. Yayınlanma tarihi: 30 Nisan 2021. Kaynak site: Big Think. bağlantı: The foundations of mathematics are unproven/
- How Gödel’s Proof Works Yayınlanma tarihi: 14 Temmus 2020. Kaynak site: Quanta Magazine. Bağlantı: How Gödel’s Proof Works
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






Sanırım Gödel’in eksiklik teorimini anlatan en açıklayıcı yazılardan, ellerinize sağlık