Düğümlenen kulaklık kabloları, modern hayatın küçük ama evrensel bir sabrını sınama testidir. En sinir bozucu yanıysa, bu kabloların nasıl kendi kendine dolaştığının hâlâ tam olarak bilinmemesidir.

Kulaklıklarınızı çantanıza özenle yerleştirirsiniz, ancak çıkardığınızda karşınıza içinden çıkılmaz bir düğüm yumağı çıkar. Cebe koymaksa daha da kötü bir fikirdir; oradan çıkardığınız karışıklığı çözmek dakikalarınızı alır. Hatta çoğu insan için bir Rubik küpünü çözmek, kulaklık kablolarını açmaktan daha kolaydır.
Bu durum yalnızca kulaklıklarla sınırlı değildir. Aynı sorun, kutuya yerleştirilen kolyelerde ya da benzer şekilde ince ve esnek nesnelerde de görülür. Beklenmedik düğümlenmeler, günlük hayatın küçük ama sabır testine dönüşen problemlerinden biri haline gelmiştir.
Kulağa önemsiz gibi gelse de bilim insanları bu sorunu ciddiye alıyor. Bunun nedeni, müzik dinleme tutkuları değil; düğüm teorisi olarak bilinen matematiksel bir alanın, bu rastlantısal düğümlenmelerin nasıl oluştuğunu anlamaya çalışmasıdır.
Düğüm Teorisi İle Düğümlenen Kulaklıkların Ne İlgisi Var?
Düğüm teorisi, ip benzeri nesnelerin kendi kendine nasıl dolaştığını inceleyerek DNA sarmallarından polimer zincirlerine kadar birçok karmaşık yapının davranışını anlamamıza yardımcı olur. İki düğümlü ip halkası düşünelim. Eğer biri, iplerin birbirinden geçmesine izin vermeden bükme, döndürme ya da kaydırma yoluyla diğerine dönüştürülebiliyorsa, bu iki düğüm eşdeğer kabul edilir.
Bu ilke, düğüm teorisinin temelini oluşturur. Bir düğümü başka bir düğüme dönüştürürken ipin kesilmesi ya da içinden geçirilmesi yasaktır. Bu sınırlı dönüşümler sayesinde düğümler matematiksel olarak sınıflandırılabilir ve aralarındaki farklar sistematik biçimde incelenebilir.

.
2007’de fizikçiler Douglas Smith ve Dorian Raymer, günlük hayatta sıkça yaşanan bu düğümlenme sorununa bilimsel bir açıklama getirmeye karar verdi. Bir ipi kutuya yerleştirip kutuyu yaklaşık on saniye boyunca salladılar. Bu basit deneyi, farklı ip uzunlukları, kutu boyutları ve sallama hızlarıyla yaklaşık üç bin kez tekrarladılar. Amaçları, iplerin kendiliğinden nasıl ve neden düğümlendiğini anlamaktı.
Sonuçlarını “The Spontaneous Knotting of an Agitated String” başlıklı makalede yayımladılar. Bulgularına göre iplerin yaklaşık yarısı, tamamen rastgele sallandığında kendiliğinden düğümleniyordu. Bu olasılığı belirleyen iki temel etken vardı: ipin uzunluğu ve sallanma miktarı.

Kulaklıklar Ne Zaman Düğümlenecektir?
Kablolar ne kadar uzun ve ne kadar çok hareket ederse, kendi kendine düğümlenme olasılığı da o kadar artar. Kablonun sertliği ya da kalınlığı da bu süreçte rol oynar, ancak en belirleyici etken uzunluk ve sallanma süresidir. Ne yazık ki bunlar da değiştirilmesi en zor faktörlerdir.
Raymer ve Smith, farklı uzunluklarda ve farklı sürelerde sallanan kablolarla yaptıkları deneylerde, 46 santimetreden kısa kabloların neredeyse hiç düğümlenmediğini buldu. Kablonun uzunluğu arttıkça düğümlenme olasılığı da yükseliyor, ancak yaklaşık 2 metreyi geçince bu artış duruyordu.
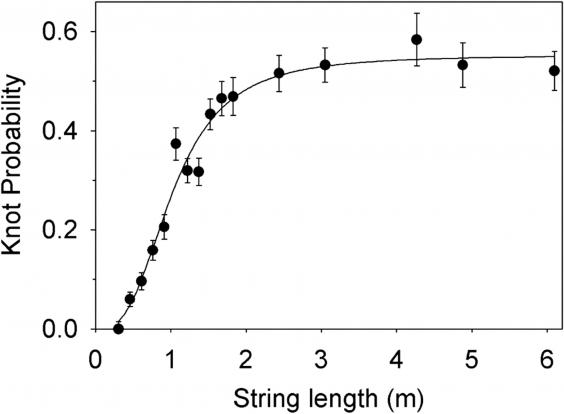
Ortalama bir kulaklık kablosu yaklaşık 139 santimetre uzunluğundadır. Bu da kulaklığınızı düğümlenmiş bulma ihtimalinizin neredeyse yüzde 50 olduğu anlamına gelir. Yani işe ya da okula vardığınızda kulaklıklarınızı çantanıza atarken, günün ilerleyen saatlerinde küçük bir sinir krizine hazırlıklı olmalısınız.
Raymer ve Smith ayrıca kulaklıkların Y biçimindeki tasarımının, düğümlenme olasılığını büyük ölçüde artırdığını belirledi. Çünkü kablonun yalnızca bir ucunun diğerinin üzerinden geçmesi, kendi kendine dolaşma sürecini başlatmak için yeterliydi.
Deneyler boyunca 120 farklı düğüm türü kaydettiler. Bunlar arasında yedi geçişli tüm temel düğüm tipleri de bulunuyordu. Bu yüzden bir dahaki sefere cebinizden birbirine dolanmış kabloları çıkarırken sinirlenmeden önce, onların bu deneydeki araştırmacılar kadar kötü durumda olmadığınızı hatırlayın.
Kaynaklar ve ileri okumalar:
- Why do your earphones get tangled in your pocket? Science has the answer; Yayınlanma tarihi: 19 Temmuz 2014; Bağlantı: Why do your earphones get tangled in your pocket? Science has the answer
- Raymer DM, Smith DE. Spontaneous knotting of an agitated string. Proc Natl Acad Sci U S A. 2007 Oct 16;104(42):16432-7. doi: 10.1073/pnas.0611320104. Epub 2007 Oct 2. PMID: 17911269; PMCID: PMC2034230.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





