Koordinatlar günlük hayatımızda önemli etkisi olan ve farkında olmadan her yerde karşımıza çıkan basit fikirlerden birisidir. Bir kağıdın üzerine bir nokta koydunuz ve bunun yerini tarif etmek istiyorsunuz diyelim. Bunu koordinatlar yardımıyla tarif edebilirsiniz. Ancak hangi koordinatlar? Kutupsal mı yoksa kartezyen mi?
Sonucunda bir değil, iki koordinat sistemi vardır. Bunlardan biri aşina olduğumuz kartezyen koordinat sistemidir. İki dik eksen çizeriz ve bir noktanın konumunu kolayca tanımlarız. Ancak bu noktayı göstermenin daha güzel bir yolu daha vardır. Bu polar koordinatlar yada diğer adı ile kutupsal koordinat sistemi sayesinde olacaktır.
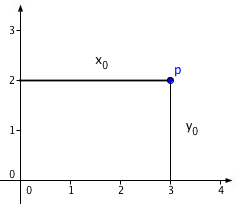
Kutupsal Koordinat Sistemi Nedir?
Kutupsal koordinat ile kastedilen aynı P noktasını merkeze (orijin) olan uzaklık ve bir açı ile göstermektir. Açıyı belirtmek için de genellikle Yunan harfi, θ (teta) kullanılmaktadır. Bu durumda bir kutupsal koordinat, (x, y) yerine (r, θ) olarak yazılmalıdır. Bu tıpkı bir aksiyon filmindeki bir denizaltının komutanının θ derecelik bir kerterizde millerce uzakta bir geminin olduğunu ilan etmesi gibi bir durumdur.
Kartezyen koordinat sistemi ile gösterilen bütün noktaları kutupsal koordinat sistemine kolayca çevirmek mümkündür. Elbette bu çeviriyi yapmak için bir miktar trigonometri bilmek gerekecektir. Bazı şekilleri kartezyen sistemde açıklamak oldukça zor iken polar koordinatlar yardımı ile bu iş oldukça kolaylaşır. Hangi şekiller bunlar derseniz mesela merkezi (0,0) ve yarıçapı 2 birim olan bir çember düşünelim. Düşünmenizi kolaylaştırmak için şekle göz atabilirsiniz. Bu çemberi iki biçimde ifade edebiliriz.
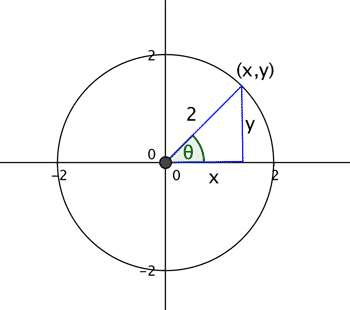
Kartezyen sistemde biraz da Pisagor teoremi yardımı ile x2+y2=4 ve polar sistemde ( 2, θ) biçiminde. Bu oldukça kolay ancak işleri biraz karıştıralım. Polar koordinatların genel olarak (r, θ) biçiminde gösterildiğini biliyoruz ya r=θ olursa yani (θ, θ) biçimli bir eğriyi çizmeye çalışırsak karşımıza nasıl bir görüntü çıkar dersiniz?
Arşimet Spirali
Unutmayalım θ bizim açımız ve bu açıyı öncelikle bir tur, yani 0 ile 2π arasında olacak biçimde alalım ve çizelim. Daha sonra açımızı 2. 3. 4. turu atacak biçimde büyütelim. Karşınıza çıkacak şeklin adı “Arşimet Spirali“dir.
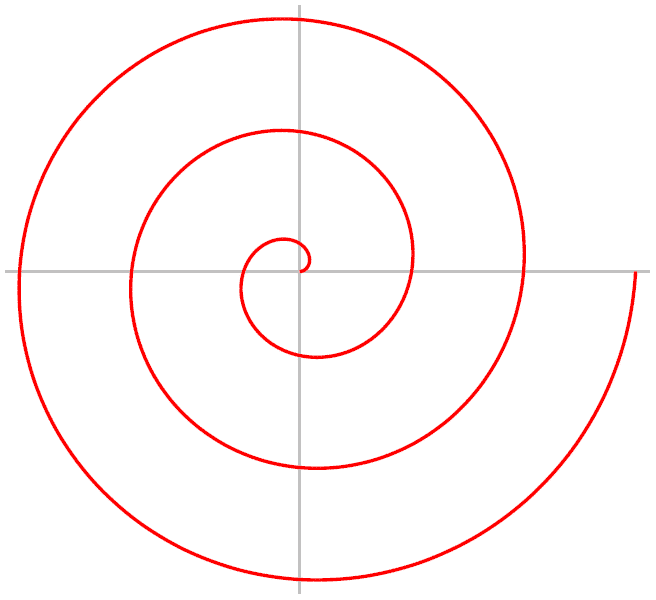
İsmini, M.Ö. 3. yüzyılda yaşamış ve Spiraller Üzerine adlı kitabında bu eğrileri incelemiş olan Yunan matematikçi Arşimet’ten alır. Gördüğünün gibi düzgün dağılım gösteren bir spiral bu, işin güzel tarafı merkezden başlayan bir doğru çizdiğinizde doğrunun spirali kestiği noktaların arası her zaman 2π kadar olacaktır. Doğal olarak bu spirali kartezyen sistemde açıklamak oldukça zordur.
Logaritmik Spiral
Kafalar biraz karıştı ise devam edelim. (r, θ) tanımımıza geri dönelim ve bu sefer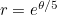 
olarak alalım. Burada bildiğiniz gibi 
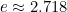değerine karşılık gelmektedir. Şimdi bu yeni koordinatlarımızı çizdiğimizde aslında karşımıza birçoğumuzun yakından tanıdığı bir şekil çıkacaktır. Öncelikle çizime bir göz atalım. İşte bu da logaritmik spiraldir. Logaritmik spiralde noktaların aralarındaki mesafeler, dışarıya doğru gidildikçe bir geometrik dizi halinde artar.
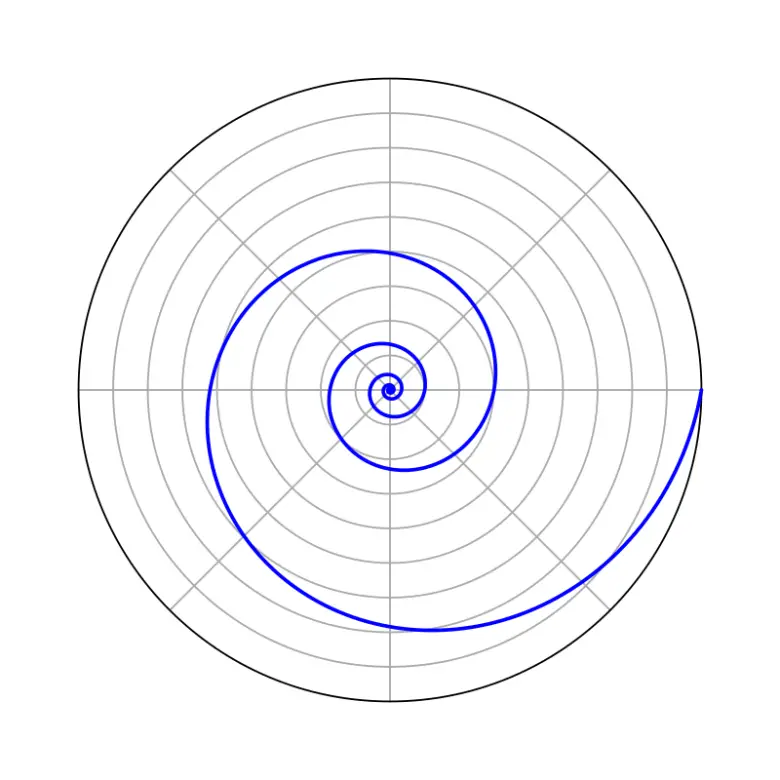
Güneş’in manyetik alanı gibi pek çok dinamik spiral ise Arşimet spiralidir. Doğada rastlanan durağan spiraller (nautilus kabuğu, sarmal galaksi, örümcek ağı, vs) logaritmik spirallerdir. Spirallerle ilgili anlatılacaklar elbette sadece bu kadar değil, ama şimdilik bu ön bilgi yeterli.
Bundan sonra ne zaman kartezyen ne zaman polar sisteme ihtiyaç duyacağınız konusunda artık daha kolay karar vereceğinizi düşünüyoruz. Yazının devamında göz atmak isterseniz: Leonardo Da Vinci Imola Kentinin Kutupsal Haritasını Nasıl Yaptı?
Kaynak: Maths in a minute: Polar coordinates; https://plus.maths.org
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel
