Johannes Kepler, gezegen hareketlerini açıklayan üç temel yasayı ortaya koyarak gökbilimde büyük bir devrim gerçekleştirdi. Kepler Yasaları, gezegenlerin nasıl hareket ettiğini açıklarken aynı zamanda Newton’un yerçekimi teorisine de zemin hazırladı.

Hepimiz zaman zaman, çevremizdeki dünyanın veya içinde bulunduğumuz evrenin büyüleyici düzeni karşısında hayranlık duyarız. Bir deniz kabuğundaki spiral şekil, bir nehrin kıvrımları ya da gökyüzünde hareket eden yıldızların uyumu… Tüm bu güzelliklerin ardında aslında matematik yatar. Bu farkındalık ise doğayı daha da etkileyici kılar.
Gezegenlerin hareketiyle matematik arasındaki ilişki de, özellikle Johannes Kepler’in (1571–1630) ilgisini çekmişti. Tezinde, Güneş’i evrenin merkezine yerleştiren, Kopernik’in 1543 tarihli heliosentrik teorisini savundu.

O dönemde bu fikir, Kilise çevrelerinde hâlâ büyük tepkiyle karşılanıyordu. Bu nedenle Kepler, düşüncelerini doğrudan aktarmak yerine bir düşünce deneyine dönüştürerek ifade etti. Kendini Ay’a yolculuk eden bir gözlemci olarak hayal etti.
Eğer Ay’a gidebilseydi, gökyüzünün orada da Dünya’dakine çok benzediğini göreceğini söyledi. Yalnızca bir fark olurdu. Ay’dan bakıldığında, Dünya da tıpkı bizim Ay’ı gördüğümüz gibi gökyüzünde hareket ediyor görünürdü. Bugün kulağa sıradan gelen bu düşünce, o dönemde hem alışılmadık hem de cesur bir çıkıştı.

Kepler’in Ay’a olan ilgisi ise yıllar içinde hiç azalmadı. 1608’de yazdığı kısa romanı Somnium (Rüya), Ay’a yolculuk fikrini ayrıntılı biçimde ele alıyordu. Bu hayal, Kepler’i gezegen hareketleri üzerine çalışmaya yöneltti.
Kepler Birinci Ve İkinci Yasasını Nasıl Buldu?
1596’da yayımladığı Magisterium Cosmographicum (Kozmografik Gizem) adlı eserinde evrenin yapısına ilişkin görüşlerini ortaya koydu. Ona göre evren, matematiksel yasalarla işliyordu. Matematiği anlayan biri, evrenin düzenini de çözebilirdi.
Kitabında, beş Platonik katının her birini bir küre içine yerleştirip bu küreleri iç içe geçiren bir evren modeli tasarladı. Her katman, o dönemde bilinen gezegenlerin Güneş çevresindeki yörüngelerine karşılık geliyordu.
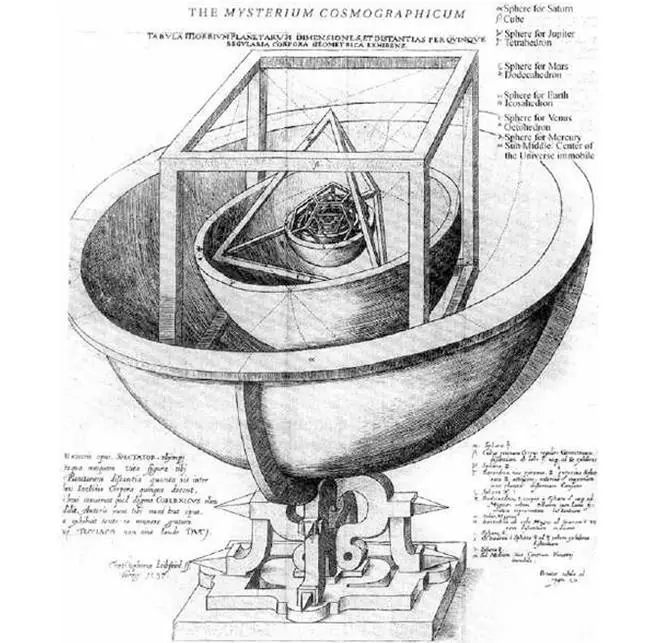
Ancak modelinde bazı sorunlar vardı. O zamana kadar gökbilimciler, gezegenlerin mükemmel daireler üzerinde hareket ettiğini varsaymıştı. Kepler kısa sürede gezegenlerin dairesel değil, eliptik yörüngelerde döndüğünü fark etti. Bir dairenin yalnızca bir merkezi varken, bir elipsin iki odağı vardır. Elips üzerindeki herhangi bir noktanın bu iki odağa olan uzaklıklarının toplamı sabittir.
Kepler, bu geometrik kavrayışı gök mekaniğine uyguladı ve gezegenlerin Güneş çevresinde elips biçiminde döndüğünü ortaya koydu. Bu keşif, Kepler’in birinci yasası olarak bilinen temel bir ilkeye dönüşerek, modern astronominin şekillenmesinde önemli bir dönüm noktası oldu.

Kepler daha sonra gezegenlerin eliptik yörüngelerde nasıl hareket ettiğini inceledi. Gözlemleri, gezegenlerin Güneş’e yaklaştıklarında daha hızlı, uzaklaştıklarında ise daha yavaş hareket ettiklerini gösterdi. Bu değişimin düzenini anlamak için gezegenin yörüngesindeki konumuna göre hızını hesapladı.
Sonuç dikkat çekiciydi: Bir gezegen, yörüngesinde hangi konumda olursa olsun, eşit sürelerde eşit alanlar tarıyordu. Yani Güneş’e yakınken daha hızlı, uzakken daha yavaş hareket ediyor ama belirli bir zaman aralığında süpürdüğü alan hep aynı kalıyordu. Bu bulgu, bugün Kepler’in İkinci Yasası olarak bilinir.
Bu iki yasa, Kepler’in yeni astronomi adını verdiği anlayışın temelini oluşturuyordu. Kepler bu bulgularını 1609’da yayımladığı Astronomia Nova adlı eserinde duyurdu. Ancak kitabın basımı maddi imkânsızlıklar nedeniyle gecikmişti ve yayımlandığında da dönemin bilim çevreleri tarafından pek ilgi görmedi. Çünkü bilim insanları henüz ne Güneş merkezli sistemi ne de gezegenlerin dairesel değil eliptik yörüngelerde döndüğü fikrini kabule hazırdı.
Kepler’in Üçüncü Yasası Nedir?
1600’lerin başında Kepler ünlü gökbilimci Tycho Brahe ile birlikte çalışıyordu. Brahe kısa süre önce Kutsal Roma İmparatoru II. Rudolf tarafından imparatorluk matematikçisi olarak atanmıştı. Bilime büyük ilgi duyan Rudolf, ondan gökyüzünde görülebilen tüm yıldızların hareketlerini içeren ayrıntılı tablolar hazırlamasını istemişti.

Kepler bu projenin matematiksel hesaplamalarında Brahe’ye yardımcı olmak üzere işe başladığında, Brahe yaşamını yitirdi. Bunun üzerine Kepler onun görevini devralarak imparatorluk matematikçisi oldu ve yaklaşık on iki yıl boyunca Prag’da kalarak bu çalışmayı sürdürdü
Kepler, yaşamı boyunca savaşlar, yoksulluk ve annesinin büyücülükle suçlanması gibi büyük sıkıntılarla karşılaşmasına rağmen, çevresindeki her şeyde bir güzellik ve düzen görüyordu. Ortaçağdan beri tartışılan “musica universalis”, yani “göksel kürelerin müziği” kavramı, ona göre evrenin derin bir uyum içinde işlediğini anlatıyordu.

Bu fikirden esinlenerek Harmonices Mundi (Evrenin Uyumları) adlı kitabını yazmaya başladı. Amacı, gezegenlerin hareketlerindeki oranların gerçekten de müzikal uyumlarla ilişkili olduğunu matematiksel olarak göstermekti.
1619’da yayımlanan bu kitapta, Dünya’nın Güneş etrafındaki hareket hızını inceledi ve bu hızın sabit olmadığını fark etti. Dünya, Güneş’e yaklaştığında daha hızlı, uzaklaştığında ise daha yavaş hareket ediyordu. Ayrıca bu değişimin oranını 16:15 olarak hesapladı. İlginçtir ki, bu oran müzikte bir yarım sese, örneğin mi ile fa arasındaki aralığa, denk gelir.
Kepler, gezegenleri bir göksel koro gibi hayal etti: Mars tenor, Satürn ve Jüpiter bas; Merkür soprano, Venüs ve Dünya ise alto olacaktı. Ona göre bu göksel koro, evrenin yaratılış anında mükemmel bir uyum içinde şarkı söylemişti.

Bu fikir hatalıydı, ancak Kepler’in bu çalışmaları son derece önemli bir matematiksel gerçeği ortaya çıkardı. Gezegenin Güneş etrafındaki dönüş süresi (yörünge periyodu), yörüngesinin büyüklüğüyle orantılıydı. Daha açık söylemek gerekirse, bir gezegenin yörünge periyodunun karesi, yörüngesinin büyük ekseninin küpüyle orantılıdır. Bu, Kepler’in Üçüncü Yasası olarak bilinir.
Sonuç Olarak
Kepler sonunda kendi ve Tycho Brahe’nin uzun yıllar süren emeğini tamamladı. Bu büyük çalışmaya onu görevlendiren Kutsal Roma İmparatoru II. Rudolf’un onuruna Rudolf Cetvelleri adını verdi. Bu eser, dönemin en kapsamlı ve en hassas astronomik hesaplamalarından biriydi.
İçinde ayrıca 1405 yıldızın konumlarını içeren bir katalog, Güneş Sistemi gezegenlerinin yerlerini bulmak için ayrıntılı yönergeler ve Ay’ın konumunu kullanarak boylam ölçmeye yarayan olağanüstü bir dünya haritası yer alıyordu.
Kepler’in hesaplamalarının ilk sınavı 7 Kasım 1631’de gerçekleşti. O tarihte Merkür’ün Güneş’in diski üzerinden geçeceğini öngörmüştü ve gerçekten de öyle oldu. Üstelik hesaplamaları yalnızca birkaç saatlik farkla doğruydu. Ne yazık ki Kepler bunu göremedi; çünkü o tarihte neredeyse bir yıldır hayatta değildi.
Sonuç olarak Kepler, çağının en büyük hesap ustalarından biriydi. Evrenin güzelliğini matematiksel yasalar aracılığıyla kavramış ve bunu olağanüstü bir öngörüyle dile getirmişti. Üstelik, gezegenlerin yörüngelerini dairesel sandığı ilk hatasından yola çıkarak düşüncelerini geliştirdi ve bu hatayı düzelterek bugün hâlâ kullanılan üç gezegen hareketi yasasını ortaya koydu.
Kaynaklar ve ileri okumalar:
- The origins of proof II : Kepler’s proofs; yayınlanma tarihi: 1 mayıs 1999. Kaynak site: Plus math. Bağlantı: he origins of proof II : Kepler’s proofs;
- Kumar, Amitabh. (2024). Proof of Kepler’s Laws through the Lens of Newtonian Dynamics. International Journal of Sustainable Applied Sciences. 2. 847-856. 10.59890/ijsas.v2i8.2316.
- Borghi, Riccardo. (2020). From Kepler’s laws to Newton’s law: a didactical proof. 10.48550/arXiv.2003.13405.
Matematiksel





