Termodinomiğin ikinci yasası bize evrendeki her şeyin düzensizliğe doğru ilerlediğini söyler. Karmaşık sistemlerde kaos kaçınılmazdır. Yani evrenin doğal olarak dağınık olması gerekir. Yine de senkronizasyon bir çok yerdedir. Ritmi olan nesneler doğal olarak senkronize olurlar.

Bir yerde bir şarkı çaldığını duyduğunuzda, kendinizi parmaklarınızı tıklatırken veya başınızı ritme göre hareket ettirirken bulabilirsiniz. Yürüyorsanız, adımlarınızın ritme uygun olması da olasıdır. Bir şekilde ne zaman hızlanacağınızı veya ne zaman yavaşlayacağınızı sezgisel olarak bilirsiniz.
Üstelik bunu yapan tek siz de değilsiniz. Bir orkestrada mükemmel bir uyum içinde çalan kemancılar. Denizde zarifçe birlikte yüzen bir balık sürüsü. Aynı duvara asılı sarkaçlı saatler de eninde sonunda senkronize olur. Hatta ateş böcekleri bile bir noktadan sonra tek bir grup olarak yanıp sönmeye başlar. Vücudunuzdaki hücreler bile şu anda bunu yapıyor ve bu oldukça şaşırtıcı.
Akıllı telefonunuz olmadan kalırsanız, enleminizi – ekvatordan ne kadar kuzeyde veya güneyde olduğunuzu – belirlemek nispeten kolay olurdu. Güneşin konumunu kullanarak bunu yapabilirsiniz. Ancak boylamınızı – ne kadar doğuda veya batıda olduğunuzu – bulmak zordur.
Boylam için sabit bir konumdaki, örneğin ayrıldığınız limandaki, saati de bilmeniz gerekir. Bu da ünlü Hollandalı fizikçi Christian Huygens’in 1656 yılında sarkaçlı saati olması ile olası olmuştur. Ancak sarkaçlar ile yaptığı çalışmalar esnasında kendisi bir de ilginç bir durumu fark etmiştir. Detayları anlamak için zamanda 350 yıl kadar geriye gitmeliyiz.
Senkronizasyon Nedir Ve Nasıl Gerçekleşir?

Huygens’in icat ettiği bir çift sarkaçlı saat duvarda yan yana asılıydı. Huygens evde dinlenmek zorunda kaldığı bir evrede, sarkaçların tam olarak uyum içinde sallandığını fark etti.
Onları senkronize olmayacak bir biçimde çalıştırmaya çabalasa da bir noktadan itibaren saatler uyum gösteriyordu. Belki de havadan gelen basınç salınımlarını senkronize ediyordu? Çeşitli deneyler yaptı. Saatlerin arasına dik bir masa koymanın senkronizasyonları üzerinde hiçbir etkisi olmadı. Ancak saatleri birbirinden uzağa veya birbirine dik açılarla astığında, kısa sürede faz dışına çıktılar.
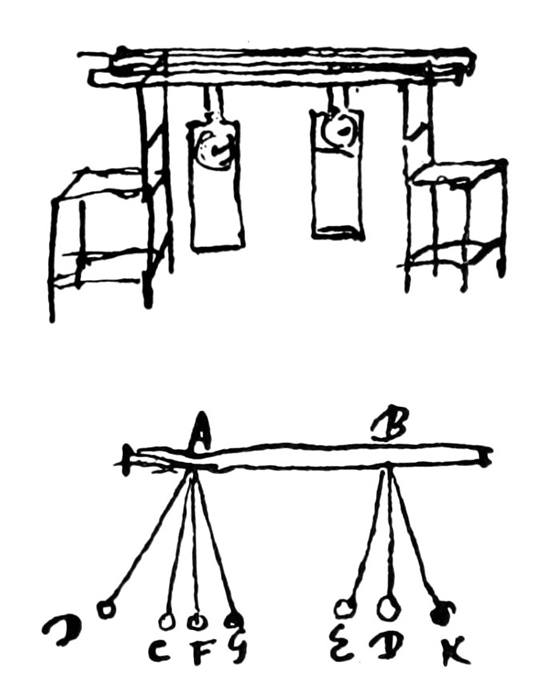
Huygens sonunda bunun nedeninin saatlerin aynı tahta çubuğa asılı olması olduğunu anlayacaktı. Bu durumda mekanik titreşimler bir saatten diğerine aktarılıyordu. Huygens cansız nesnelerde kendiliğinden senkronizasyonu gözlemleyen ilk kişi olacaktı. Günümüzde, garip fenomeni açıklayacak matematiksel araçlara sahip olmasa da altta yatan mekanizmayı doğru bir şekilde anladığını biliyoruz.
Başka bir Hollandalı, Engelbert Kaempfer, 1690’da Tayland’a seyahat etti ve ateş böceklerinin birbirlerine uyumlu bir biçimde parıldadığını gözlemledi. 1920’lerde radyo mühendisleri, farklı frekanslara sahip elektrik jeneratörlerini birbirine bağlamanın, onları ortak bir frekansta titreşmeye zorladığını keşfettiler.

Bunu sizler de gözlemleyebilirsiniz. Bir kaç tane metronumu hafif sallanan bir platforma, senkronize olmayacak bir biçimde yerleştirdiğinizde, bir zaman sonra senkronize olduklarını görmeniz neredeyse büyülü bir deneyim olacaktır.
Metronomlar Nasıl Senkronize Olur?
Bu metronomlar tam olarak aynı doğal frekansa sahip olmasalar da, metronomların salınımları üzerinde durdukları platformu bir miktar hareket ettirir. Sonunda bu hareket bir uyum yakalamalarına neden olur. Kaç tane metronomunuz olursa olsun sonuç değişmeyecektir. Aşağıda 100 metronomun uyum için salınımını görüyorsunuz.
Bireyler sadece belirli basit kuralları takip ederse, sistem düzeyinde senkronizasyonun belireceği aşikârdır. Örneğin, bir balık sürüsünde bulunan balıklar için basit kurallar şöyle olabilir. Çevrenizdeki balığa yakın durun (ama çok yakın değil), yakınınızdakilerle aynı yönde hareket edin ve bir yırtıcı geldiğinde yoldan çekilin.
Bu üç kuralı takip eden nesneler bize tanıdık gelen üşüşmek ve toplanmak gibi davranışlar sergiler. Boid algoritması, bu tür davranışları gerçekçi bir şekilde taklit etmek için kullanılır. Tek bir balık, daha büyük resimde ne yaptığını bilmez. Sürünün kolektif hareketi kavramına sahip değildir. Ayrıca komuta merkezi de yoktur. Yine de basit kurallar ile senkronizasyon gerçekleşir.
Aynısı ateşböcekleri, cırcır böcekleri ve hatta senkronize ateşlenen nöronlar için de geçerlidir. Biyolojik ayrıntılar büyük ölçüde farklı olsa da küresel senkronize yanıt olgusu aynıdır. 1960’ların ortalarında matematikçi-biyolog Art Winfree, biyolojideki kitlesel senkronizasyon örneklerinin listesinden etkilenerek, senkronizasyon için kriterlerin ne olduğunu anlamak için çalışmalara başladı.
Winfree bu yönde çok ilerleme kaydetti ancak denklemleri çok karmaşıktı. 1974’te Yoshiki Kuramoto adlı bir Japon fizikçi matematiği nasıl basitleştirebileceğini gördü. Kuramoto’nun modeli, bir osilatör popülasyonunu (metronomlar ve kalp atışları gibi ritimleri olan şeyler) tanımladı ve neden kendiliğinden senkronize olduğunu gösterdi.
Kuramoto Modeli Nedir?

O zamanlar 34 yaşında olan Kuramoto, modelini disiplindeki uzmanlara gösterdiğinde, önemini kavrayamadılar. Cesaretini yitiren Kuramoto, çalışmayı bir kenara bıraktı. Beş yıl sonra Winfree, Kuramoto’nun çalışmasına rastladı ve çalışmanın önemini hemen anladı.
Kuramoto modelinde, komşularıyla aynı hizada olma eğiliminde olan, osilatör adı verilen soyut saatlerden faydalanmıştı. Kuramoto’nun yaptığı, osilatörlerin hızlarını simetrik, ikili bir şekilde sadece göreli fazlarına bağlı olarak ayarladıklarını varsayarak Winfree’nin orijinal modelini basitleştirmekti.
Çalışması senkronizasyonun ileri fazdaki osilatörün hızını azaltması ve gerideki diğerine yetişine kadar hızını arttırması sonucu olduğunu gösteriyordu. Kendisi ayrıca bu dinamiğini tanımlamak için bir dizi diferansiyel denklem formüle etmişti. Denklemler tüm osilatörlerin tamamen aynı olduğunu ve diğerlerine benzer şekilde bağlı olduğunu varsayıyordu.
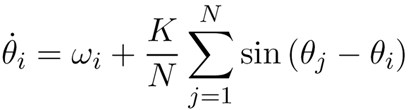
Senkronizasyon bilim insanlarının ilgisini her daim çekmiştir ve bu durumu açıklamak için bir çok matematiksel model tanımlanmıştır. Geliştirilen modellerden Yoshiki Kuramoto tarafından önerilen Kuramoto Modeli yapılan çalışmalarda en çok tercih edilendir.
Sonuç Olarak
Kuramoto Modeli, karmaşık bir sistemdeki karmaşık davranışları yakalayabilen basit bir matematiksel sistemin güzel bir örneğidir. Ancak biyolojik senkronizasyon biraz daha karmaşıktır.
Matematik denklemlerindeki soyut osilatörlerin aksine, ateş böcekleri bilişsel varlıklardır. Karmaşık duyusal bilgileri birleştirir ve bunları bir karar alma hattı aracılığıyla işlerler. Ayrıca sürekli hareket halindedirler, akranlarıyla görsel bağlar kurarlar. Basitleştirilmiş matematiksel modeller henüz bu karmaşıklıkları yakalayamıyor.
Kaynaklar ve ileri okumalar
- Synchrony with chaos – blinking lights of a firefly swarm embody in nature what mathematics predicted. Yayınlanma tarihi: 16 kasım 2022. Kaynak site: Conversation. Bağlantı. Synchrony with chaos – blinking lights of a firefly swarm embody in nature what mathematics predicted
- The mathematical explanation for “spontaneous synchronization”. Yayınlanma tarihi: 19 Kasım 2022. Kaynak site: Big Think. Bağlantı: The mathematical explanation for “spontaneous synchronization”
- Peña, Jonatan & Nijmeijer, Henk. (2020). The secret of the synchronized pendulums. Physics World. 33. 36-40. 10.1088/2058-7058/33/1/28.
- Acebrón, Juan A. et al. “The Kuramoto model: A simple paradigm for synchronization phenomena.” Reviews of Modern Physics 77 (2005): 137-185.
- Winfree AT. Biological rhythms and the behavior of populations of coupled oscillators. J Theor Biol. 1967 Jul;16(1):15-42. doi: 10.1016/0022-5193(67)90051-3. PMID: 6035757.
Matematiksel






