Hayatımız düzensizdir. Doğal fenomenlerin pek çoğu düzensizdir. Ancak düzensiz sistemler de bile bazen bir düzen bulabiliriz. İngiliz matematikçi ve filozof Frank Plumpton Ramsey’in (1903-1930) adını taşıyan Ramsey teorisi, sistemlerde düzen ve örüntü bulmakla ilgilenir.

Diyelim ki bir doğum günü partisi planlıyorsunuz ve davetli listesi üzerinde kafa yoruyorsunuz. Kime davetiye göndermelisiniz? Hangi arkadaş ve yabancı kombinasyonu doğru bir karışımdır? Bu size basit bir sorun gibi gelebilir ancak matematikçiler bu problemin bir versiyonu üzerinde neredeyse bir yüzyıldır çalışıyorlar.
Matematikçilerin bulmaya çalıştığı şey “bir yapıda belli bir özelliğin var olması için en az kaç eleman kullanılması yeterlidir?” sorusunun cevabı. Plumpton Ramsey 27 yaşında hayatını yitirse de, temellerini attığı bu teorisinin günümüzde birçok uygulama alanı vardır.

Birazdan okuyacağınız gibi teorinin temel fikirlerini anlamak oldukça kolaydır. Öte yandan, bazı olağanüstü zor soruları da gündeme getirdiği için aynı zamanda aktif bir araştırma alanıdır. Sorduğu temel soru şudur. Düzensiz ve karmaşık bir sistemde her zaman bir düzen var mıdır? Eğer öyleyse, içinde belirli bir düzen bulabileceğimizden emin olmak için düzensizliğin boyutu ne olmalıdır?
Düzensizlikten Düzene Geçiş
İçinde altı kişinin olduğu bir oda olduğunu varsayalım. İki kişi birbirini tanıyorsa arkadaş, tanımazlarsa yabancı diyelim. Kuşkusuz en düzenli durum, altı kişinin ya tamamen arkadaş ya da tamamen yabancı olması olurdu. Ancak insanlar rastgele seçildiği için muhtemelen odada arkadaş ve yabancılar karışık biçimde olacaktır.
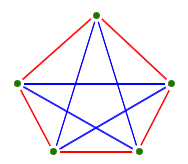
Odadaki her bir insan çiftini birleştiren çizgiler çizdiğimizi ve ikisi arkadaşsa maviye, yabancıysa kırmızıya boyadığımızı varsayalım. Grafik oldukça karışık gözüküyor. Ama yine de odada en azından hepsi arkadaş ya da tamamen yabancı olan üç kişiyi bulabilir miyiz?
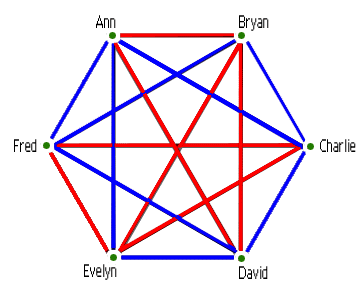
Şaşırtıcı bir şekilde, oradaki üçer kişiden oluşan bir grupta, ya herkesin birbirini tanıdığından ya da daha önce tanışmadıklarından emin olabiliriz. Şekle baktığınız zaman üç kenarı mavi ve 3 kenarı kırmızı olan üçgenler göreceksiniz. 6 kişide en az bir tane böyle bir üçgen bulmak mümkündür. Örneğin şeklimizde Charlie, Evelyn ve Fred birbirlerine yabancıdırlar. Çünkü bu üçlünün oluşturduğu üçgenin üç kenarı da kırmızıdır.
Kağıt ve renkli kalemlerle denemeler yapmak, altı kişiyle her zaman tek renkli bir üçgen olduğuna bizi ikna edecektir. Ancak ikna olmak yetmez. Bunun doğru olduğunu nasıl kanıtlayacağız? Bunun bir yolu, olası tüm seçenekleri listelemek ve sırayla her birini kontrol etmek olacaktır. Ne yazık ki 30.000’den fazla olası seçenek olduğu düşünülünce bu biçimde bir kanıt yapmak fazla da eğlenceli değildir. Neyse ki, bunu çok daha kolay kanıtlayabiliriz.
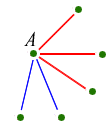
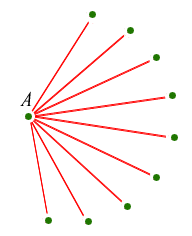
6 kişimize geri dönelim. Sonucunda bir kişinin 5 tane arkadaşı olabilir. Yani Bir A noktası düşündüğümüzde bundan beş tane çizgi çıkmalıdır. Tamamen arkadaş ya da tamamen yabancı 3 kişi arıyoruz. Bu nedenle beş çizgide bir renkten en az üç tane olmalıdır. Yani bir noktadan çıkan en az üç kırmızı çizgi veya en az üç mavi çizgi vardır.
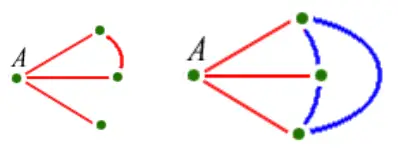
Diyelim ki üç kırmızı çizgi var. Kalan üç çizgi hangi renklerde olacaktır? Bunlardan biri bile kırmızı olursa A noktası (solda) ile birlikte kırmızı bir üçgen oluşturur. Aksi halde üçü birlikte mavi bir üçgen oluşturacaktır.(sağda).
Ramsey Sayıları Ve Ramsey Teorisi Nedir?
Yukarıda altı noktayla her zaman tek renkli bir üçgen olması gerektiğini kanıtladık. Diğer bir deyişle,” Üçünün arkadaş ya da üçünün yabancı olduğundan emin olmak için en az kaç kişiye ihtiyacımız var?” sorusunun cevabını bulduk. Bu bizim ilk Ramsey sayısı örneğimizdir ve R(3,3)olarak yazılır.
Altı kişinin kesinlikle yeterli olduğunu gördük; başka bir deyişle, R(3,3) 6’dan büyük değildir. Aynı zaman da 6’dan da küçük olamaz. Bunu anlamak için aşağıdaki grafiğe göz atın. Gördüğünüz gibi beş kişi ile böyle bir sonuca ulaşmak mümkün değildir. Bu durumda R(3,3)=6 olmalıdır.
Şimdi başka bir Ramsey sayısı ile uğraşalım. R(4,4) ifadesi bize ya 4 ortak arkadaş ya da 4 ortak yabancı bulma konusunda emin olmak için kaç kişiye ihtiyaç olduğunu söyler. Bunu hesaplamak kolay değil. Bu nedenle işe R(3,4)’ü bularak başlayalım.
Yani “hepsi mavi çizgilerle birbirine bağlı üç nokta, ya da hepsi kırmızı çizgilerle bağlı dört nokta bulmayı garanti etmek için kaç noktaya ihtiyacımız var?” sorusunun cevabını arayalım. Bu yukarıda aktardığımız ispata benzer bir biçimde yapılır (İspatı burada vermeyeceği, merak edenler kaynağı inceleyebilir). Bunun sonucunda da R(3,4)=9 bulunur. Şimdi bu bilgiyi R(4,4) bulmak için kullanabiliriz.
İlk olarak, dört arkadaş veya dört yabancıyı garanti etmek için 18 kişinin yeterli olduğunu iddia edelim. Bir nokta alalım ve 17 çizgi çizelim. Bu çizgilerden en az 9 tanesi aynı renk olmalıdır. R(4,3)=9 olduğunu zaten biliyoruz. Yani bu 9 nokta arasında ya dört arkadaş ya da üç yabancı olmalıdır.
Üç yabancı varsa, A’da bu kişilere yabancı olduğundan toplam dört yabancımız var. Yani ya dört arkadaşımız ya da dört yabancımız var. Bu da iddia ettiğimiz şeydir. R(4,4) kesinlikle vardır ve en fazla 18’dir. Ayrıca 17 nokta da böyle bir kümeyi oluşturmak için yeterli değildir. ( Neden derseniz ispatı oldukça uzun ve burada). Sonuç olarak R(4,4)=18’dir.
Daha Büyük Ramsey Sayıları
Yukarıda R(3,4) ve R(4,3) için sınır koyabildiğimiz zaman R(4,4)’ü hesaplayabileceğimizi anlatmaya çalıştık. Aslında R(3,3) ve R(2,4)’e sınır koyabildiğimiz zaman R(3,4)’ü hesaplayabiliriz. Matematiksel gösterimde, hem R(a-1,b) hem de R(a,b-1) var olduğu sürece R(a,b)’nin var olduğunu bulabiliriz. Bu ilişkiyi aşağıda görebilirsiniz. Bu mantıkla R(5,5), R(6,6) ve diğer Ramsey sayıları mevcut olmalıdır. Ramsey teorisi bize verilen grafik yeterince büyük olduğu sürece istediğimiz düzeni bulabileceğimizi söyler.
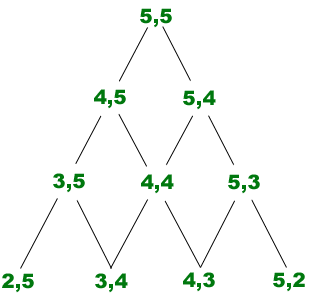
Peki R(5,5)’in değeri nedir? Kimse bilmiyor! Aslında, çok az sayıda Ramsey R(a,b) sayısı bilinmektedir. R(3,3)=6, R(4,3)=9 ve R(4,4)=18, R(5,3)=14, R(6,3)=18 ve R(7,3)=23 bildiklerimizdir. Mevcut bilgilerimizle R(5,5) hakkında söyleyebileceğimiz en fazla şey, 42 ile 55 arasında bir yerde olduğudur.
Konu ilginizi çekti ise bir gelişme için göz atabilirsiniz: 90 Yıl Sonra Matematikçiler Ramsey Sayıları İle İlgili Problemi Çözdüler
Kaynaklar ve ileri okumalar için:
- Imre Leader; Friends and strangers; Yayınlanma tarihi: 1 Aralık 2000; Kaynak site: Plus Math. Bağlantı: Imre Leader; Friends and stranger/
- Ramsey Theory Extracts Order from Chaos when Sorting through Confusing Arrangements of Numbers. Kaynak site: Scientific American. Yayınlanma tarihi: 8 Kasım 2022; Bağlantı: Ramsey Theory Extracts Order from Chaos when Sorting through Confusing Arrangements of Numbers/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel