Katı cisimlerin hacim formülleri genelde basit olmasına rağmen, bazı durumlarda karıştırılabilir. Özellikle küre gibi geometrik şekillerin hacim ve yüzey alanı formülleri, prizma, piramit veya koni kadar akılda kalıcı olmayabilir. Ancak, size göstereceğimiz yöntemlerle kürenin hacim ve yüzey alanı formüllerini kolayca hatırlayabilirsiniz.

Bunun için en baştan başlamamız gerekiyor. Önce katı cisimleri üç ana kategoriye ayıralım: prizmalar, sivri cisimler ve küre. Şimdi sırasıyla bunların ne olduğunu ve hacim formüllerini inceleyelim.
Prizmalar
Prizmalar, taban alanı ve yüksekliği bilindiğinde kolayca hesaplanabilen cisimlerdir. Tabanı kare ise kare prizma, tabanı üçgen ise üçgen prizma, tabanı daire ise silindir denir.

Prizmalar, dik ve eğik olarak iki gruba ayrılır. Ancak her iki türde de hacim formülü aynıdır. Bir prizmanın hacmi, taban alanının yükseklik ile çarpılmasıyla hesaplanır. Kavramı daha iyi anlamak için bir görselden faydalanabilirsiniz.
Sivri Cisimler (Piramit ve Koni)
Sivri cisimler, prizmalara benzer şekilde tabanlarına göre adlandırılır. Tabanı kare olan bir sivri cisme kare piramit, tabanı üçgen olan bir sivri cisme üçgen piramit, tabanı daire olan bir sivri cisme ise koni denir. Bu isimlendirme, cismin temel geometrik yapısını anlamayı kolaylaştırır.

Sivri cisimlerin en belirgin özelliği, tabanın bir noktaya doğru daralmasıdır. Bu nokta, cismin tepe noktası olarak adlandırılır. Bu yapı, onları prizmalarla karşılaştırıldığında daha ince ve sivri bir görünüme kavuşturur.
Sivri cisimlerin hacmi, taban alanı ile yüksekliğinin çarpımının üçte biri olarak hesaplanır. Buradaki yükseklik, tabanın tam merkezinden tepe noktasına kadar olan dik mesafeyi ifade eder. Bu “üçte bir” oranı, tamamen sivri cisimlerin daralan geometrik yapısından kaynaklanır. Bir piramit, aynı taban alanına ve yüksekliğe sahip bir prizmanın içine yerleştirildiğinde, prizmanın hacminin yalnızca üçte birini kaplar.
Küre
Katı cisimler konusunda bir sonraki bilmeniz gereken şekil küredir. Kürenin formülleri, prizma ve sivri cisimlerden farklı bir mantığa dayanır. Kürenin hacmi, tabanı ve yüksekliği kürenin çapına eşit olan iki koninin hacimleri toplamına eşittir.
Bu ilişki, kürenin geometrik yapısını anlamanıza yardımcı olur ve formülü akılda tutmayı kolaylaştırır. Öncelikle bu şekli inceleyiniz. Sonrasında, bu formülün neden doğru olduğunu ve nasıl ortaya çıktığını birlikte anlamaya çalışalım.
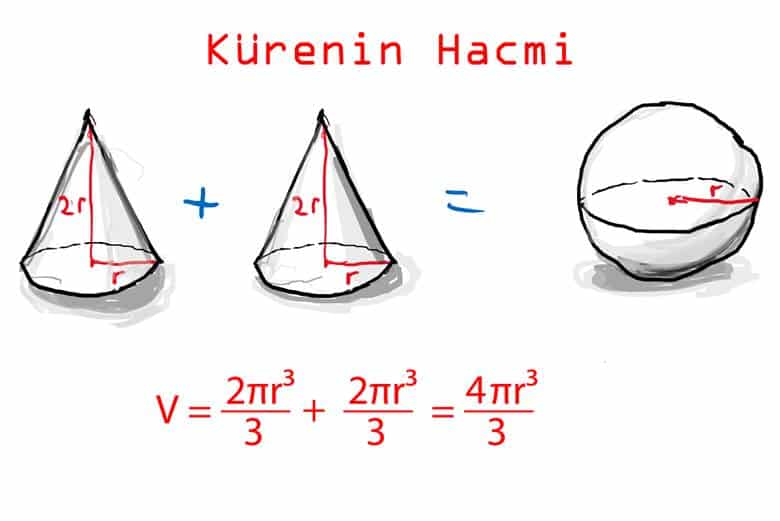
Aslında, bir kürenin hacim formülünü belli geometrik cisimler yardımıyla siz de ispatlayabilirsiniz. Bunun için, yukarıda özelliklerini anlattığımız bir koniye ve bu koninin yüksekliğiyle eş bir çapa sahip olan bir küreye ihtiyacınız olacak. Ayrıca, koninin yarıçapı ile kürenin yarıçapının da birbirine eşit olması gerekir.
Bir kürenin hacmini belirleyen ilk kişi, antik dönemin büyük matematikçisi Arşimet idi. Arşimet, bu sonuca aynı taban alanına sahip bir silindir, koni ve küreyi kullanarak ulaştı. Deneyinde, şekillerin içinin tamamen dolu ve aynı homojen maddeden yapıldığını kabul etti. Maddenin yoğunluğunu 1 kabul ederek, ağırlığın hacimle aynı olduğunu varsaydı. Böylece kürenin hacmini, bu diğer şekillerle kıyaslayarak buldu.
Bir Kürenin Alanı Neden Bir Dairenin Alanının 4 Katıdır?
Bir kürenin yüzey alanının bir dairenin alanının 4 katı olması, geometri ve matematiğin derinliklerinde yatan bir ilişkidir. Bu bağlantı ilk bakışta tesadüfi gibi görünebilir, ancak aslında kürenin simetrik yapısına ve matematiksel hesaplamalara dayanır.
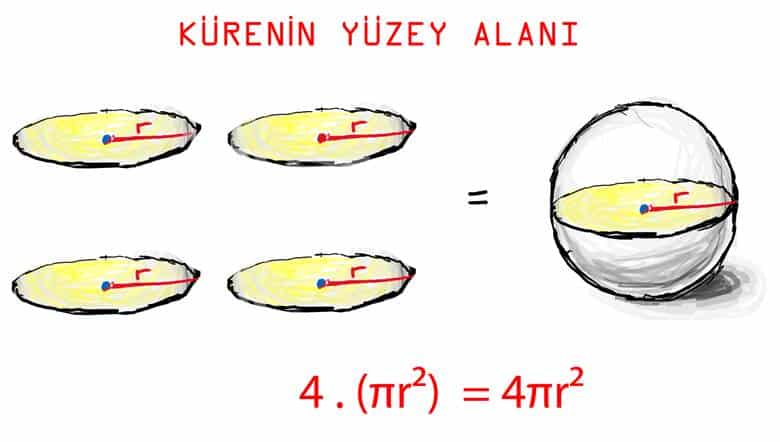
Bu ilişki, kürenin yüzey alanını integral yoluyla hesapladığımızda ortaya çıkar. Kürenin yüzeyi, sonsuz küçük alan parçalarının toplamıdır. Hesaplama sürecinde, bu parçaların toplamının tam olarak dört çemberin alanına eşit olduğu görülür. Yani, kürenin yüzeyi dört eşit daireyle örtüşecektir.
Arşimet, bu ilişkiyi ilk fark eden bilim insanlarından biriydi. Bir kürenin yüzey alanının, aynı çapta bir silindirin dış yüzeyi ile eşit olduğunu göstermişti (kapaklar hariç). Bu, kürenin yüzey alanını anlamada büyük bir ilerleme sağlamıştı. Bu buluş, aynı zamanda bir çemberin alanının kürenin alanıyla nasıl ilişkilendiğini anlamamızı kolaylaştırmıştır.
Kürenin yüzey alanını daha iyi anlamak için kürenin etrafına bir silindir yerleştirdiğimizi hayal edelim. Bu silindir, küreyle aynı yükseklikte ve aynı yarıçapta olmalıdır. Şimdi bu silindirin açık halini düşünelim. Elimizde bir dikdörtgen olacaktır.
Bu dikdörtgenin kısa kenarı kürenin yüksekliği ve uzun kenarı ise kürenin çevresi kadar olmalıdır. Bizim yapmamız gereken sadece uzun ve kısa kenarı çarpmak ve bunun sonucunda bir kürenin yüzey alanının nasıl hesaplandığını anlamaktır.

Gördüğünüz gibi, katı cisimlerin formülleri birbiriyle yakından ilişkilidir. Kürenin yüzey alanı, bir daire, bir silindir ve hatta bir koniyle ilişkilendirilebilir. Bu nedenle, bu temel formülleri öğrenmek, diğer geometrik cisimlerin hesaplamalarını anlamayı ve öğrenmeyi de kolaylaştırır.
İspatlar için kaynaklar ve izleme önerileri:
- But why is a sphere’s surface area four times its shadow?; https://www.youtube.com/
- Visualizing the Volume of a Sphere Formula; https://www.youtube.com/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





