Weierstrass fonksiyonu gibi yapılar, karmaşık hareketi modellemek için son derece uygundur. Ancak tıpkı Karl Weierstrass’ın kendisi gibi, bu fonksiyonun etkileri de zamanla ortaya çıkmıştır.
Karl Weierstrass (1815-1897), modern matematiğin temellerini atan ve kalkülüsün kesin bir şekilde tanımlanmasını sağlayan Alman matematikçidir. “Modern analiz” olarak bilinen alanın kurucularından biri kabul edilen Weierstrass, özellikle türevlenebilirlik ve süreklilik kavramlarına getirdiği açık ve kesin tanımlarla tanınır.
Kalkülüs, matematikte güçlü bir araçtır. Ancak 17. yüzyılda ortaya çıkışından sonra, uzun yıllar boyunca sezgilere ve resmi olmayan yöntemlere dayanarak kullanıldı. Bu durum, teorik açıdan bazı belirsizlikler doğurdu.
Fransız matematikçiler, bu belirsizlikleri sorgulamak yerine kalkülüsü fiziksel problemlere uygulamayı tercih etti. Gezegenlerin yörüngelerini hesaplamak, elektrik akımlarını incelemek ya da mekanik sistemlerin hareketini analiz etmek gibi alanlara yöneldiler.
Öte yandan, 19. yüzyılda Alman matematikçiler bu yaklaşımı yeterli bulmadı. Kalkülüsün temelini oluşturan varsayımları yeniden değerlendirmeye başladılar. Daha önce doğru kabul edilen noktaları sorguladılar. Bu süreçte karşı örnekler üreterek teoriyi yeniden yapılandırdılar. Bu yeni yaklaşımın öncülerinden biri Karl Weierstrass’tı
Kısaca Karl Weierstrass Kimdir?

Ölüm: 19 Şubat 1897, Berlin, Almanya
Weierstrass, küçük yaşlardan itibaren matematiğe olan yeteneğini gösterdi. Ancak babası, onun kamu maliyesi ve yönetim eğitimi almasını istedi. Üniversite derslerinden sıkılan Weierstrass’ın zamanının büyük bölümünü içki içerek ve eskrim yaparak geçirdiği anlatılır.
1830’ların sonlarında diplomasını alamadan üniversiteden ayrıldı. Bunun üzerine bir ortaokulda öğretmenlik yapmaya başladı. Matematik ve fizik gibi alanların yanı sıra, güzel yazı ve beden eğitimi gibi çok farklı dersler de verdi. Profesyonel bir matematikçi olarak kariyerine ancak 40 yaşına yaklaşırken adım attı. Buna rağmen, matematikte derin bir dönüşüm yarattı ve büyük bir etki bıraktı.
1872 yılında yayımladığı bir makalede, sürekli olmasına rağmen hiçbir noktada türevlenemeyen bir fonksiyon tanımladı. Bu, o döneme kadar geçerli kabul edilen kalkülüs anlayışını kökten sarstı. Matematikçiler bu örneğe başlangıçta büyük tepki gösterdi. Ancak Weierstrass’ın tanımladığı bu “matematiksel canavar”, kalkülüsün temellerini daha sağlam hâle getirme sürecini başlattı.
Süreklilik ve Türevlenebilirlik Nedir?
Sürekli bir fonksiyon, adından da anlaşılacağı gibi, tanım kümesinde herhangi bir noktada ani bir kopma ya da sıçrama göstermeyen fonksiyondur. Bu tür fonksiyonlar, grafik üzerinde kesintisiz bir şekilde ilerler. Yani, fonksiyonun bir noktasından diğerine geçerken kalemi kaldırmadan çizim yapabilirsiniz. Bu durum, fonksiyonun belirli aralıklar içinde tutarlı bir şekilde değiştiğini gösterir.
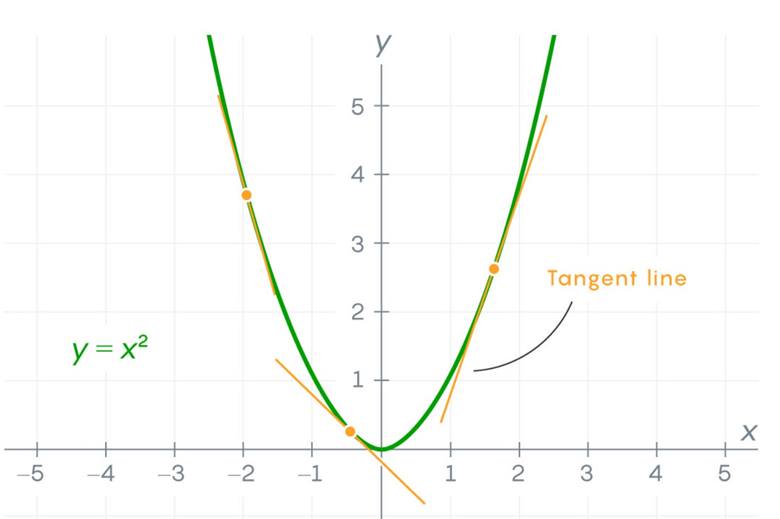
Kalkülüs, temel olarak sürekli fonksiyonların ne kadar hızlı değiştiğini anlamaya çalışır. Bir fonksiyonun grafiği üzerinde herhangi bir noktada bir teğet çizdiğinizde, bu çizginin eğimi o noktadaki anlık davranışı gösterir. Eğimin pozitif olması, fonksiyonun o noktada yukarı yönlü hareket ettiğini; negatif olması ise aşağı yönlü hareket ettiğini gösterir.
Bu noktada devreye türev girer. Türev, bir fonksiyonun belirli bir noktadaki anlık değişim hızını ölçen matematiksel bir araçtır. Daha sade bir ifadeyle, türev bir fonksiyonun o noktadaki eğimini temsil eder. Türev sayesinde, bir fonksiyonun o anda ne kadar hızlı artmakta ya da azalmakta olduğunu anlayabiliriz.
Eğer bir fonksiyonun türevi tanım kümesindeki her noktada mevcut ise, o fonksiyon türevlenebilir kabul edilir. Türevlenebilirlik, fonksiyonun sadece sürekli olmasıyla değil, aynı zamanda değişim hızının da düzgün ve tanımlı olmasıyla ilgilidir. Kesintilere sahip (discontinuous) fonksiyonlar hiçbir zaman türevlenebilir değildir. Bir fonksiyonda boşluk ya da sıçrama varsa, o noktada teğet çizgisi belirlenemez. Bu da türevin tanımsız olduğu anlamına gelir.
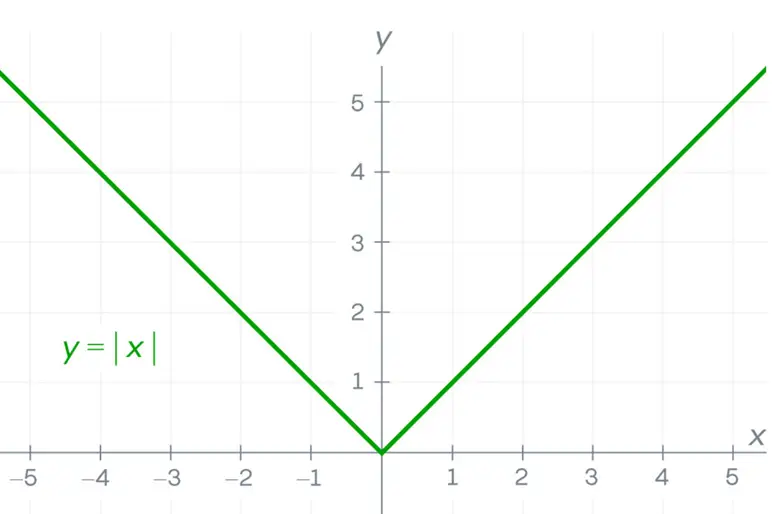
Ancak, ilginç bir şekilde, sürekli olan tüm fonksiyonlar da türevlenebilir değildir. Örneğin, mutlak değer fonksiyonu (|x|) her noktada süreklidir. Yani grafik üzerinde kalemi hiç kaldırmadan çizebilirsiniz. Fakat x = 0 noktasında eğri ani bir dönüş yapar. Bu keskin dönüşte, eğim bir anda yön değiştirir. Dolayısıyla burada teğet çizilemez ve fonksiyon o noktada türevlenemez. Bu, sürekliliğin türevlenebilirlik için gerekli ama yeterli bir koşul olmadığını gösterir.
Weierstrass’ın “Canavar” Fonsiyonu Nedir?
19. yüzyılın başlarında çoğu matematikçi bu durumu ciddi bir problem olarak görmüyordu. Bu tür örneklerin istisna olduğunu, yalnızca belirli birkaç noktada ortaya çıktığını düşündüler. “Fonksiyon yeterince düzgünse, türevin tanımsız olduğu yerler yalnızca birkaç özel nokta olur,” görüşü hâkimdi.
Hatta 1806’da, ünlü Fransız matematikçi ve fizikçi André-Marie Ampère, bu fikri matematiksel olarak kanıtladığını öne sürdü. Ampère’e göre, sürekli bir fonksiyon yalnızca sınırlı sayıda noktada türevlenemezdi.
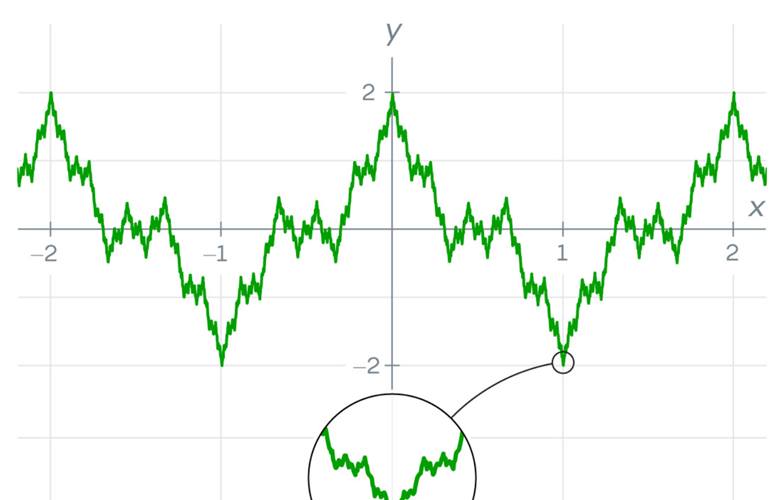
Ancak bu görüş, Karl Weierstrass sahneye çıktığında kökten sarsılacaktı. Weierstrass, Ampère’nin ispatına göre mümkün olmaması gereken bir fonksiyon keşfetti. Weierstrass, bu şaşırtıcı fonksiyonu, sonsuz sayıda dalga benzeri kosinüs fonksiyonunu üst üste ekleyerek oluşturdu. Her yeni terim eklendikçe fonksiyon daha fazla zikzak yapmaya başladı. Sonunda, her noktada yön değiştiren, sonsuz derecede tırtıklı bir testere dişine benzeyen bir yapı ortaya çıktı.
Birçok matematikçi bu fonksiyonu ciddiye almadı. Fakat Weierstrass, bu fonksiyonun hiçbir noktada türevlenemez olduğunu tartışmasız biçimde ispatladı. Bu ispatı yapmak için, Augustin-Louis Cauchy ve Bernard Bolzano gibi matematikçilerin onlarca yıl önce geliştirdiği süreklilik ve türevlenebilirlik tanımlarını yeniden değerlendirdi.
O dönemde bu tanımlar, belirsiz ifadeler ve tutarsız sembollerle yapılmıştı ve yanlış yorumlanıyordu. Bu nedenle Weierstrass, önceki tanımları baştan yazdı. Belirsiz ifadeler yerine kesin dil ve net matematiksel formüller kullandı. Bugün her kalkülüs öğrencisinin öğrendiği epsilon-delta ile limit tanımı, aslında Weierstrass’ın geliştirdiği modern versiyona dayanır.
Weierstrass, bu tanımı hem süreklilik hem de türevlenebilirlik kavramlarının temeli olarak kullandı. Bu buluş, sürekliliğin türevlenebilirlik anlamına gelmediğini gösterdi. Matematikçiler bu yeni kavramı, o dönemde “canavar” olarak adlandırdı.
Weierstrass Fonksiyonunun Mirası
Weierstrass’ın ispatı, kalkülüsün artık yalnızca geometrik sezgilere dayandırılamayacağını açıkça ortaya koydu. Newton ve Leibniz gibi kurucuların sezgisel yaklaşımları yerini, denklemlerin titiz analizi üzerine kurulu yeni bir standart anlayışa bıraktı.
Bu gelişmeyle birlikte, matematikçiler Weierstrass’ın izinden gitmek zorunda kaldılar. Fonksiyon kavramını daha kesin tanımladılar. Süreklilik ile türevlenebilirlik arasındaki ilişkiyi yeniden değerlendirdiler. Türev ve integral alma yöntemlerini daha sağlam temellere oturttular.
Kalkülüsün bu şekilde standartlaştırılması süreci zamanla analiz adı verilen yeni bir matematik dalına dönüştü. Weierstrass da bu alanın kurucularından biri olarak kabul edildi. Onun çalışmaları, yalnızca belirli bir problemi çözmekle kalmadı; modern matematiğin düşünme biçimini kökten değiştirdi.
Weierstrass’ın fonksiyonunun mirası, yalnızca kalkülüs ve analiz alanlarının temellerini güçlendirmekle kalmadı. Aynı zamanda, matematiğin beklenmedik yapılar ve sezgiye aykırı örneklerle dolu olduğunu da ortaya koydu. Bu keşif, matematiksel dünyada saklı duran “canavarların” varlığını görünür kıldı, Weierstrass fonksiyonu, bu “canavarlar” arasında öncüdür. Bu yapı, aynı zamanda fraktal geometrinin erken örneklerinden biri olarak da görmektedir.
Weierstrass’ın fonksiyonu, yalnızca kuramsal bir meydan okuma olarak kalmadı. Zamanla pek çok pratik uygulama alanı olduğu da ortaya çıktı. 20. yüzyılın başlarında fizikçiler, Brown hareketini yani, sıvı ya da gaz içindeki parçacıkların rastgele hareketini, incelemek istiyordu.

Bu hareket süreklidir ama düzgün değildir. Çok hızlı ve sonsuz derecede küçük dalgalanmalarla karakterize edilmektedir. Weierstrass fonksiyonu gibi yapılar, bu karmaşık hareketi modellemek için son derece uygundu.
Benzer şekilde, bu tür fonksiyonlar insan davranışındaki belirsizlikleri, karar alma süreçlerini ve risk alma eğilimlerini modellemek için de kullanıldı. Ayrıca finansal piyasaların karmaşık, öngörülemez dalgalanmalarını anlamada da önemli bir araç haline geldi. Tıpkı Weierstrass’ın kendisi gibi, bu fonksiyonun etkileri de zamanla ortaya çıktı. Ancak, bu buluşun etkileri matematiği ve onun uygulamalarını bugün hâlâ şekillendirmeye devam ediyor.
Kaynaklar ve ileri okumalar
The Jagged, Monstrous Function That Broke Calculus. Yayınlanma tarihi: 12 Ocak 2025. Kaynak site: Bağlantı: The Jagged, Monstrous Function That Broke Calculus
Matematiksel






