17. yüzyılda matematikçiler, henüz keşfedilmemiş bir matematik kıtasını, adeta Yeni Dünya’yı keşfeder gibi buldular. Bu kıtanın adı Calculus (kalkülüs) idi ve iki büyük kaşifi vardı: Isaac Newton ve Gottfried Wilhelm Leibniz.
Calculus, matematikçilere ve bilim insanlarına değişen nicelikleri ifade edebilecekleri güçlü bir dil sundu. Temel Teorem ise, bu değişimleri anlamada ve çözüm üretmede etkili bir araç sağladı. Modern bilim bu araçlar olmadan düşünülemez.
Ne var ki, ironik bir şekilde, günümüz matematikçileri artık “calculus” terimini nadiren kullanır. Bu alanda yapılan çalışmalar, genel olarak analiz başlığı altında toplanır. Analiz ise Gerçek Analiz, Karmaşık Analiz, Fonksiyonel Analiz gibi alt dallara ayrılır.

Kalkülüs Fikri Nasıl Gelişti?
Bugünden baktığımızda, Avrupalı matematikçilerin 17. yüzyıl boyunca Calculus’a adım adım yaklaştığını açıkça görebiliriz. Bu ilerleyiş, iki farklı çizgi üzerinden şekilleniyordu. İlki, quadrature (alan hesabı) olarak bilinen; biçimi düzensiz, çoğunlukla eğri kenarlı bölgelerin alanını hesaplama problemiydi.
Bu konu, antik çağlardan beri matematikçileri büyülemiştir. İlk yöntemler, bir şekli kesip yeniden düzenlemeye dayanıyordu. Daha sonra, Antik Yunan’da Arşimet ve Çin’de Liu Hui gibi matematikçiler, bu alanda daha rafine yaklaşımlar geliştirdiler. Eğri bölgeleri giderek daha iyi uyum sağlayan çokgenlerle yaklaşık olarak ifade ederek alan hesaplarını daha doğru hale getirdiler.
1600’lü yılların başında, İtalyan matematikçi Bonaventura Cavalieri, “bölünemezler yöntemi” olarak adlandırılan sistematik bir teknik geliştirdi. Bu yöntem, bilinmeyen bir alanı ince dikdörtgen dilimlere ayırıp bu dilimlerin alanlarını toplayarak sonuca ulaşmayı hedefliyordu.
Aslında, Arşimet de buna benzer bir yöntem geliştirmişti. Ancak bu çalışma zamanla kaybolmuş, ancak 1906 yılında yeniden keşfedilmiştir. Bu nedenle Avrupa bilim tarihini etkileme şansı olmamıştır. Hem Cavalieri hem de Arşimet, bu yaklaşımı pratik bir hesaplama aracına dönüştürmeyi başaramamıştır.
Calculus’a giden ikinci yol, eğri bir çizgiye teğet çizme problemleriyle başladı. Bu tür problemler, dönemin koşullarında birden fazla yaklaşıma ihtiyaç duyuyordu.
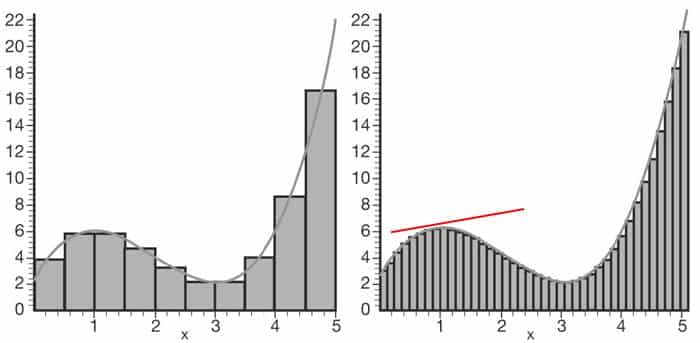
Eğimi hesaplamak için, eğri üzerinde incelenen noktaya çok yakın başka bir nokta düşünülürdü. Bu iki nokta arasında bir doğru parçası çizilir ve bu doğrunun eğimi hesaplanarak yaklaşık bir sonuç elde edilmeye çalışılırdı.
Ancak elde edilen değer her zaman belli bir hata payı içerirdi. Eğer ikinci noktayı “sonsuz derecede yaklaştırmak” ve doğru parçasını “sonsuz derecede kısa” hale getirmek mümkün olsaydı, tam eğim değeri bulunabilirdi. Ne var ki bu süreci matematiksel olarak temellendirmek zordu; çünkü bu işlem özünde sıfırı sıfıra bölmeye çalışmak anlamına geliyordu.
Newton ve Leibniz Kalkülüs’ü Nasıl Buldu?

Bazı kişiler, büyük olasılıkla Newton’un Cambridge’deki hocası Isaac Barrow da dahil, hem alan bulma hem de teğet çizme problemleri üzerinde çalışmıştı. Ancak bu iki problemin aslında aynı kavramın iki farklı yönü olduğunu fark eden yalnızca Newton ve Leibniz oldu.
Bu iki eski problemin birbiriyle ilişkisi, ilk bakışta oldukça keyfi ve yapay görünen bir adımla ortaya çıkmıştı: Eğrileri grafiklere dönüştürmek. Günümüzde grafik kavramı neredeyse herkesin aşina olduğu bir araçtır, ancak 17. yüzyılda bu fikir hâlâ oldukça yeniydi.
Newton ve Leibniz, böylece matematiğe iki temel kavram kazandırdı: Teğet problemini çözen türev ve alan bulma problemini çözen integral. Her ne kadar bu kavramların öncülleri daha önce ortaya atılmış olsa da, kimse bunların birbiriyle ters işlemler olduğunu fark etmemişti.
Bu ters ilişkiye bugün Calculus’un Temel Teoremi diyoruz. Günümüzde bu ilişkiyi aşağıdaki formülle ifade ederiz.

İlginçtir ki Newton, “flüksiyonlar yöntemi” adını verdiği yaklaşımını paylaşma konusunda oldukça ketumdu. Temel Teoremi büyük olasılıkla 1664 ile 1666 yılları arasında keşfetmişti; ancak bu çalışmalarını yalnızca birkaç kişiye ve parça parça göstermeyi tercih etti.
O dönemde matematikçiler, bilimsel ilerlemenin en güvenilir yolunun bilgileri gizlemek değil, yayımlamak olduğunu henüz kavrayamamıştı.
Sonuçta Kalkülüs’ü Kim Buldu?

Leibniz, 1670’lerde değişim hızları ve sonsuz toplamlar üzerine düşünmeye başladığında, Newton’un bu konularla ilgili çalışmalarını dolaylı yollardan duymuştu. Newton, sonsuz toplamlar, alan hesapları ve yay uzunlukları gibi problemleri çözebildiğini söylüyordu. Leibniz de 1673 ile 1675 yılları arasında bir noktada Temel Teoremi çözmeyi başardı.
Bunun üzerine Newton’la iletişime geçerek, onun bu konularda tam olarak ne bildiğini öğrenmek istedi ve bir tür bilgi alışverişi önerdi. “Sen bana bunu açıkla, ben de sana başka bir şey anlatayım.”
Newton ise son derece ihtiyatlı davrandı ve Leibniz’e yalnızca iki mektup yazdı. İkinci mektubunda Calculus’un Temel Teoremini verdi, ancak bunu anlaşılması neredeyse imkânsız bir anagramın içine gizledi. Bu durum, Newton’un keşfini gerçekten paylaşmak istemediğini açıkça gösteriyordu.
Leibniz, Calculus üzerine yaptığı çalışmayı 1684’te Nova Methodus adlı eserinde yayımladı. Newton ise şaşırtıcı biçimde, “flüksiyonlar yöntemi”ni anlatan ilk metnini ancak 1704’te yayımladı.
Bunun ardından, Calculus’un gerçek mucidinin kim olduğu üzerine son derece sert bir tartışma başladı. İngiliz matematikçiler Newton’u, kıta Avrupası’ndaki bilim insanları ise büyük ölçüde Leibniz’i destekledi. Her iki taraf da birbirini intihalle suçladı.
Sonuç Olarak
Modern tarihçilerin ortak görüşüne göre, her iki taraf da hem haklı hem de haksızdı. Aslında ortada bir intihal yoktu; iki matematikçi de aynı keşfi birbirlerinden bağımsız olarak gerçekleştirmişti. Temel Teoremi ilk fark eden kişi Newton’du, ancak Calculus’u dünyaya ilk duyuran kişi Leibniz’di.

Leibniz’in kullandığı sembollerin çok daha sade ve pratik olması sayesinde, bugün kullandığımız notasyon neredeyse tamamen ondan miras kalmıştır. Artık kimse Newton’un “flüksiyon” ve “flüent” terimlerini kullanmaz; bu sözcükler, Newton’la birlikte tarihe karışmıştır.
Kaynaklar ve ileri okumalar
- Stefan Buijsman; Pluses and Minuses: How Math Solves Our Problems; ISBN-10 : 0143134582;
- Lu, Jiachen. (2023). Who Contributed More on Calculus? Newton or Leibniz?. Studies in Social Science & Humanities. 2. 22-25. 10.56397/SSSH.2023.07.04.
- What Is Calculus? Definition and Practical Applications. Kaynak site: Thought. Yayınlanma tarihi: 24 Temmuz 2024. Bağlantı: What Is Calculus? Definition and Practical Applications
Matematiksel





