Fields Madalyası, matematik dünyasının en prestijli ödüllerinden biridir. Her dört yılda bir, 40 yaşın altındaki dört matematikçiye verilir. 2022 yılında bu ödülü kazananlardan biri de 39 yaşındaki June Huh oldu. Ancak onun hikayesi diğer matematikçilerin hikayelerinden biraz farklı. Çünkü Huh, üniversite hayatının altıncı yılına kadar matematiği pek de sevmeyen biriydi.

Aslına bakarsanız, June Huh’un eğitim hayatı boyunca matematik notları pek parlak değildi. Hatta bu yüzden lise yıllarında şair olmayı bile düşünmüştü. Öğrencilik hayatı boyunca matematikten kaçınmak için elinden geleni yaptı. Ancak bir tesadüf, onun bu kaçışını tersine çevirdi. Matematiğe olan ilgisini uyandıran şey, bizzat matematiğin kendisi değil, bir insandı.
Parlak matematikçilerden bahsedildiğinde, genellikle yüksek notlar, kazanılan ödüller ve olağanüstü bir çalışma azmi akla gelir. Ancak June Huh, bu tanımlamaların hiçbirine uymuyordu. Eğer matematikle ilgili zorluklar yaşıyorsanız, onun hikayesi size aradığınız ilhamı verecektir.
June Huh Matematiği Sevmeyi Nasıl Başarmıştı?
Aslında June Huh öğrenmeyi seviyordu, ancak sınıf ortamında bir konuya odaklanmak ya da derslerden öğrendiklerini aklında tutmakta zorlanıyordu. Bunun yerine, kendi kendine kitap okumayı ve evlerinin yakınındaki dağda yürüyüşe çıkmayı tercih ediyordu.
Belki de okuduğu kitapların etkisiyle, ilerleyen süreçte şair olmak yerine bilim yazarı olmaya karar verdi. Bu hedefle Seul Ulusal Üniversitesi’nde Fizik ve Astronomi dersleri almaya başladı. Ancak başlangıçta bu dersler de onun ilgisini pek çekmedi. Ta ki, 1970’te Fields Madalyası sahibi matematikçi Heisuke Hironaka’nın dersine katılana kadar. Bu ders, onun hayatını tamamen değiştirecekti.

Huh, kısa sürede karizmatik bir akademisyen olan Hironaka’nın etkisine kapıldı. Ancak onu büyüleyen sadece hocasının karizması değildi; matematiğin kendisi de ilgisini çekmeye başlamıştı.
“Cebirsel Geometriye Giriş” dersi, aslında cebirsel denklemlerin çözümlerini ve bunların geometrik özelliklerini incelemeye yönelikti. Ancak Hironaka, dersin standart içeriğini takip etmek yerine, belirli uzay türlerine odaklanan tekillik kuramı üzerine kendi araştırmalarını anlatıyordu. Başlangıçta iki yüz öğrenciyle dolu olan sınıf, konuların karmaşıklığı arttıkça hızla azaldı. Sonunda derste sadece beş öğrenci kaldı ve Huh da onlardan biriydi.
Bu, onun için bir dönüm noktasıydı. Hayatında ilk kez, matematiksel bir araştırmanın nasıl şekillendiğini ve geliştiğini gerçek zamanlı olarak izliyordu. Ders, yalnızca var olan bilgilerin aktarılmasından ibaret değildi. Hironaka, bizzat üzerinde çalıştığı problemlerin çözüm sürecini öğrencileriyle paylaşıyor, henüz kesinleşmemiş fikirleri sınıfta tartışıyordu.
Geleneksel matematik derslerinden tamamen farklı olan bu deneyim, Huh’un matematiğe bakışını değiştirmeye başladı. Matematik, onun için artık soyut ve sıkıcı bir ders olmaktan çıkmış, keşfedilmeyi bekleyen dinamik bir alan haline gelmişti. Böylece, yıllarca matematikten uzak duran June Huh, hiç tahmin etmediği bir şekilde, en büyük tutkularından birini keşfetmiş oldu.
June Huh’a Fields Madalyası Kazandıran Çalışması Neydi?

Matematik alanında derinlemesine bir eğitim almamış olan Huh, kariyerine kendi deyimiyle “çıplak gözle görülebilen” nesnelere odaklanarak başladı. Bu doğrultuda, kombinatorik üzerine çalışmalara yöneldi.
Matematikte somut nesnelerle ilgilenen bir diğer alan ise geometridir. Geometrik nesneleri tanımlamak için cebirsel denklemler kullanan matematik dalına ise cebirsel geometri denir. Huh, çalışmalarında kombinatorik ile cebirsel geometri arasında köprüler kurmaya odaklanmaya başladı.
Matematikte büyük ilerlemeler genellikle birbirinden bağımsız gibi görünen alanlar arasında bağlantılar kurulduğunda gerçekleşir. Huh’un başarısı da tam olarak bunun bir kanıtıydı. Matematiğe duyduğu ilgiyi artık tamamen bu yönde şekillendirmiş, kısa sürede alanında fark yaratan bir isim olmayı başarmıştı.
Huh, henüz Illinois’de doktora öğrencisiyken graf (çizge) kuramındaki 40 yıllık bir problem olan “Read’in kestirimi”ni ispatlamayı başardı. Ortaya koyduğu çözüm, matematik camiasında büyük yankı uyandırdı. Daha önce doktora başvurusunu reddeden Michigan Üniversitesi, bu başarısından sonra Huh’ı doktora programına kabul etti.
June Huh’un Fields Madalyası kazanmasını sağlayan çalışmaları oldukça karmaşıktır. Bu nedenle, kısa ve basit bir açıklama yapmak kolay değildir. Ancak en azından çalışmalarının hangi konuyla ilgili olduğu hakkında genel bir fikir edinebiliriz.
Okul yıllarından hatırlayacağınız gibi, y = x² fonksiyonu bir parabolü ifade eder. Bir parabolün en önemli özelliklerinden biri, yalnızca bir minimum noktasına sahip olmasıdır. Aşağıdaki çizimde maviyle gösterilen bu nokta, eğrinin en düşük değer aldığı yerdir. Bir fonksiyon, grafiği yukarıya doğru eğiliyorsa konveks fonksiyon olarak adlandırılır. Daha basit bir ifadeyle, bir fonksiyonun herhangi iki noktası arasındaki doğru parçası, fonksiyonun grafiğinin üstünde kalıyorsa bu fonksiyon konvekstir.
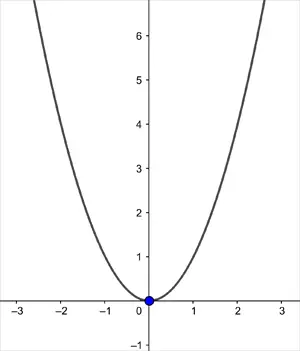
Ancak aşağıda gösterilen eğrinin iki yerel minimum değeri vardır. Aşağıdaki örnek ise, konveks olmayan bir fonksiyondur.
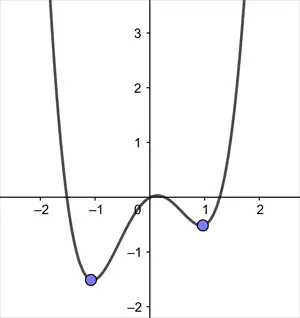
Konveks Fonksiyonlar Önemlidir
Konvekslik kavramı, bir fonksiyonda birden fazla değişken olduğunda da mevcuttur. Bunları görselleştirme kolay olmasa da hesaplanması mümkündür.
Bir araba yaptığınızı ve yakıt tüketimini en aza indirmek istediğinizi düşünelim. Size çeşitli değişkenler cinsinden yakıt tüketimini açıklayan matematiksel bir fonksiyon verilirse, işiniz bu fonksiyonun minimumunu bulmaktır. Ancak muhtemelen birçok değişkenden oluşan karmaşık bir fonksiyona bakıyor olursunuz.
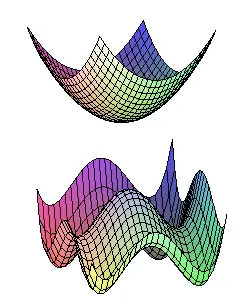
Konveks analiz, matematiğin optimizasyon, fonksiyonel analiz ve ekonomi gibi birçok alanında kullanılan bir dalıdır. Temel olarak konveks fonksiyonlar ve konveks kümeler üzerine çalışır. Konveks fonksiyonlar, optimizasyon teorisinde çok kullanışlıdır çünkü konveks bir fonksiyonun yerel minimum noktası, aynı zamanda global minimumdur. Bu özellik, karmaşık problemlerin çözümünü kolaylaştırır.
Konveks analiz yalnızca sürekli fonksiyonlarla ilgilenir. Oysa gerçek dünyadaki birçok problem sürekli değil, kesiklidir. Bu gibi durumlar, yalnızca konveks analizin değil, aynı zamanda kesikli matematik ve kombinatorik tekniklerin de devreye girmesini gerektirir. İşte June Huh ve meslektaşlarının yaptığı şey de tam olarak bu noktada önem kazanır: sürekli fonksiyonlar ile kesikli yapıları birleştirmek.
Sonuç olarak
June Huh tutkusunu keşfetmiş ve bunu daha da ileri götürmeyi başarmıştı. Onun hikayesi ve başarısı, matematikle sorun yaşadığı için bu alandan uzak duran herkese ilham verecek niteliktedir.
Hayatınızı değiştiren bir kitabın ya da ilham verecek bir kişinin ne zaman ve nerede karşınıza çıkacağını bilemezsiniz. Bu yüzden, öğrenmeye, araştırmaya ve yeni keşiflere açık olmaya devam ediniz. Ayrıca göz atmak isterseniz: 2022 Fields Madalyası Kazanan Maryna Viazovska İle Tanışın
Kaynaklar ve ileri okumalar
- He Dropped Out to Become a Poet. Now He’s Won a Fields Medal. Yayınlanma tarihi: 5 Temmuz 2022; Bağlantı: https://www.quantamagazine.org
- The Fields Medals 2022: June Huh. yayınlanma tarihi: 1 Temmuz 2022; Bağlantı: https://plus.maths.org/content/jh
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel








