Her şey bir olasılıktır ve her yeni bilgi, olasılıklarımızı güncellememizi sağlar. Bunun ilk kez Fransız matematikçi Joseph Louis François Bertrand (1822–1900) tarafından, 1889 yılında yayınlanan “Calcul des probabilités” adlı kitabında ortaya atılan güzel bir örneği vardır ve dilimizde Üç Kutu Paradoksu adı ile bilinmektedir.
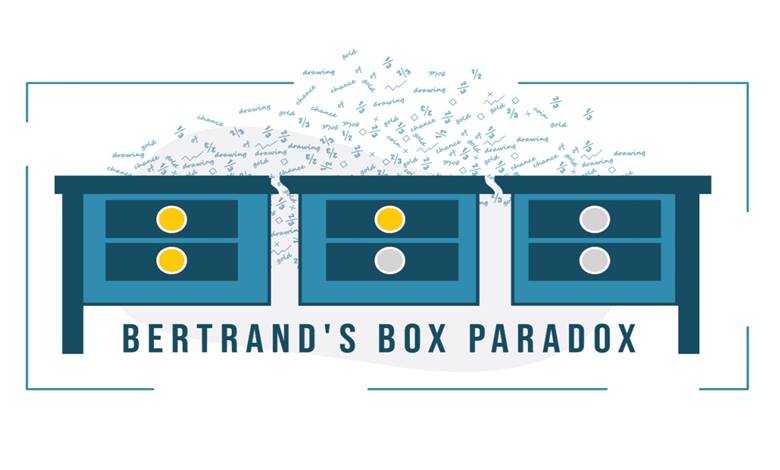
Paradoks Monty Hall problemine benzer bir biçimde, içerikleri başlangıçta bilinmeyen ve dışarıdan bakıldığı zaman birbiri ile aynı gözüken üç kutuyla başlar. Kutuların her birinde iki çekmece vardır. Bir kutunun iki çekmecesinin her birinde birer altın bulunur ( AA). İkinci kutunun iki çekmecesinde de birer gümüş para bulunur (GG). Üçüncü kutuda ise bir çekmecede gümüş para, diğer çekmecede de altın var(AG) .
Şimdi gelişigüzel bir kutu seçelim. İki bölmesinden rastgele birini açtığımızda içinde altın para olduğunu görüyorsak diğer bölmesinde de altın para olma olasılığı diğer bir deyişle AA ikilisini seçmiş olma olasılığımız nedir? Cevaba geçmeden önce biraz düşünmenizi öneriyoruz. Tamam yeterince düşündüm diyorsanız cevaba geçelim…
Üç Kutu Paradoksunun Çözümünü Neden Yanlış Anlıyoruz?
Üç kutudan herhangi birini seçme olasılığı diğerleriyle aynıdır. Bu olasılık da 1/3 kadardır. Eğer seçilen kutunun bir çekmecesinde altın bulmuşsak o zaman içinde iki gümüş para bulunan kutuyu seçmemişiz demektir. Yani içinde iki altın ya da bir altın bir de gümüş para bulunan kutulardan birini seçtik. Bu iki kutuyu da seçmenin olasılığı aynı olduğuna göre, diğer çekmecedeki paranın da altın olmasının olasılığı bu durumda 1/2 yani yüzde 50’dir. (Değildir!)

Doğru cevap aslında 2/3 olacaktır ve bunu anlamak için biraz düşünmemiz gerekecektir. Bir kutunun bir çekmecesini açtığımızda ve içinde de bir tane altın para olduğunu gördüğümüz de, aynı kutunun diğer çekmecesinde de diğer altın veya gümüş olma olasılığa bulunduğunu ve bu durumda altın para seçme olasılığının 1/2 yani yüzde 50 olduğunu düşünme eğiliminde oluruz.
Sonunda iki seçenekten birini seçeceğimizi düşünürüz. Ancak aslında bu düşünce biçimimiz hata yapmamıza neden olur. Oysa ki her ne kadar başlangıçta AA ve AG kutularını seçme olasılığı aynı olsa da AA kutusunu seçersek altın bulma olasılığınız %100 ve AG kutusunu seçersek altın bulma olasılığınız %50 olacaktır.
Paradoksun Doğru Çözümü Nasıl Olmalıdır?
Doğru cevap için şu biçimde düşünmeliyiz. Bir altın para çektiğinizi biliyorsunuz. Bu durumda seçilen altın para, AG kutusunun G çekmecesinden seçilemez. Bununla beraber GG kutusundaki iki çekmeceden de seçilmiş olması olası değildir. Demek ki bu para AG kutusunun ya A çekmecesinden gelmiş olmalı ya da AA kutusunun herhangi iki çekmecesinden gelmiş olmalıdır. Bu üç olasılık da eşit dağılıma sahiptir. Demek ki altının çekildiği çekmecenin AA kutusundan gelmiş olma olasılığı 2/ 3 olmalıdır.
Kaynaklar ve ileri okumalar
- Britannica, The Editors of Encyclopaedia. “Joseph Bertrand”. Encyclopedia Britannica, 17 Apr. 2024, https://www.britannica.com/biography/Joseph-Bertrand. Accessed 5 May 2024..
- The Easiest Problem Everyone Gets Wrong. Kaynak site: Youtube. – Vsauce. Bağlantı: https://www.youtube.com/watch?v=ytfCdqWhmdg
- Saenen L, Heyvaert M, Van Dooren W, Schaeken W, Onghena P. Why Humans Fail in Solving the Monty Hall Dilemma: A Systematic Review. Psychol Belg. 2018 Jun 1;58(1):128-158. doi: 10.5334/pb.274. PMID: 30479812; PMCID: PMC6194549.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





