“Chinese Stick Multiplication” adıyla bilinen ve çubuklar yardımıyla yapılan Çin çarpma tekniği ( Japon çarpma tekniği olarak da bilinir) geleneksel çarpma yöntemlerine ilginç ve etkili bir alternatif sunar.

Yöntemin temelleri oldukça basittir ve günümüzde kullandığımız çarpma algoritmalarına benzer şekilde çalışır. Ancak en büyük avantajı, çarpma işlemini görselleştirme imkânı sunmasıdır. Bu özelliği sayesinde özellikle öğrenme sürecinde oldukça etkili bir araçtır.
Çin’de (veya Japonya’da) bu yöntem, ilköğretim düzeyinde çocuklara çarpma kavramını daha iyi kavratmak amacıyla hala öğretilmektedir. Ayrıca, yöntemin öğrenme üzerindeki olumlu etkileri yapılan araştırmalarla da desteklenmiştir
Çin Çarpma Tekniği Nedir?
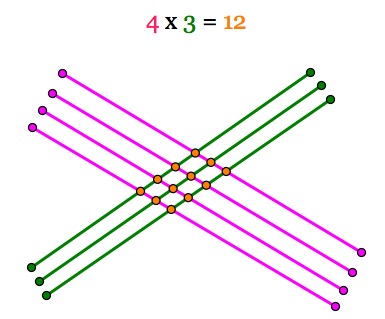
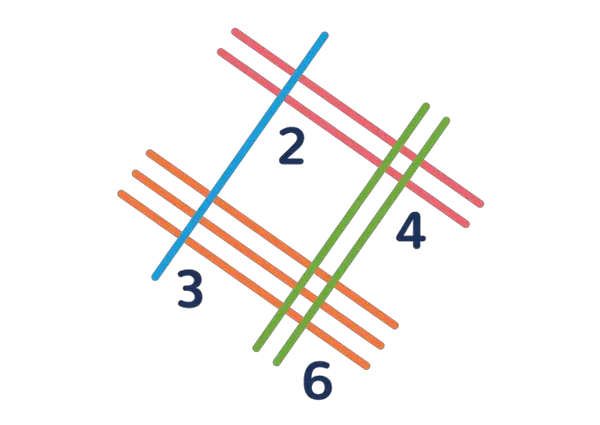
Bu yöntemle bir çarpma işlemini yalnızca birkaç doğru çizerek ve kesişme noktalarını sayarak kolayca hesaplayabilirsiniz. Örneğin, 4 ile 3’ü çarptığımız bir durumu ele alalım. Bu örnek için aşağıdaki görseli düşünebiliriz:
- Dört pembe çizgi sayısı “4”ü temsil eder.
- Üç yeşil çizgi ise “3”ü temsil eder.
Bu iki grup çizginin kesiştiği noktalar, çarpımın sonucunu verir. Bu durumda, dört pembe çizgi ile üç yeşil çizginin kesiştiği 12 turuncu nokta oluşur. Kesişen noktaları saydığımızda, 12 sonucuna ulaşıyoruz. Bu basit ama etkili görselleştirme yöntemi, çarpma işlemini öğrenmeyi ve anlamayı kolaylaştırır.
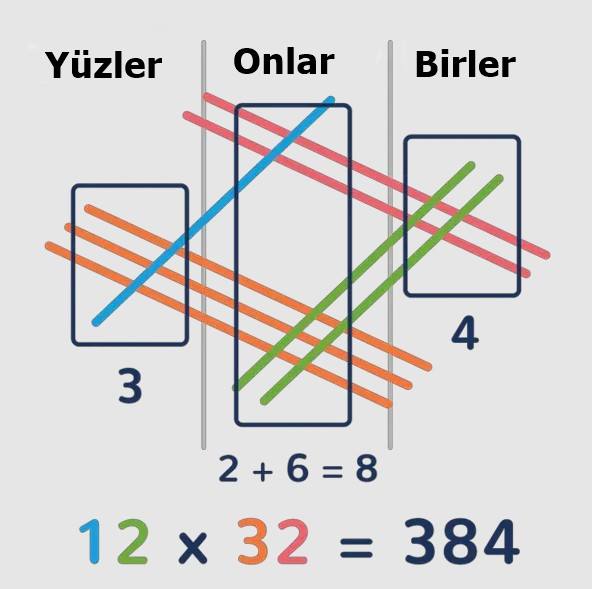
Şimdi iki basamaklı bir çarpma işlemini inceleyelim. Örnek olarak 12 × 32 işlemine bakalım. Bu yöntemde Sayıların basamak değerleri çizgilerle temsil edilir. Yani; 32 sayısı, üç tane “on” (3 çizgi) ve iki tane “bir” (2 çizgi) ile 12 sayısı, bir tane “on” (1 çizgi) ve iki tane “bir” (2 çizgi) olarak ifade edilir.
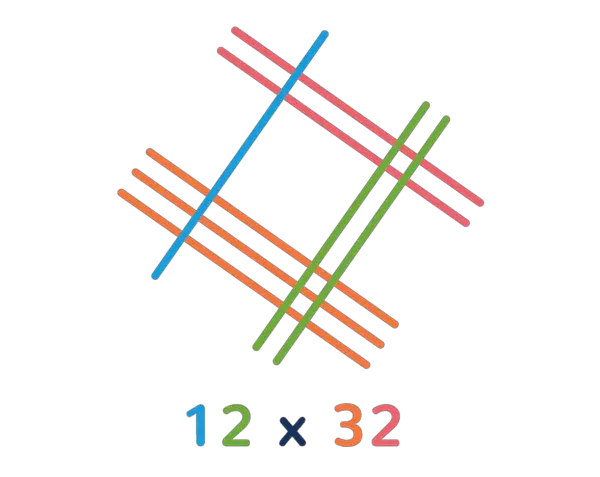
Çizgilerin kesişim noktaları farklı basamaklara (yüzler, onlar, birler) göre sayılır. Bu kesişim sayıları toplanarak çarpım sonucu elde edilir.
Şimdi kesişim noktalarını yukarıdan aşağıya doğru gruplamanız gerekiyor. Bu gruplamada asıl yaptığınız şey ise yüzler, onlar ve birler basamağını hesaplamak oluyor. İstenilen sonuca ulaştığımızı aşağıda görebilirsiniz.
Çin Çarpma Yöntemi Neden İşe Yarıyor?
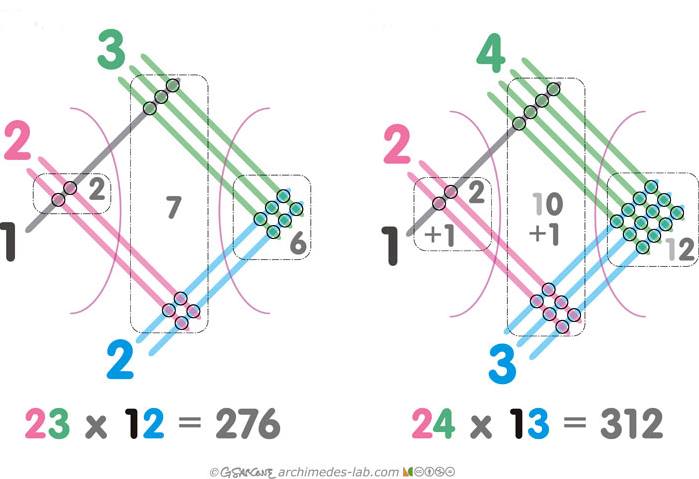
Aslında bu sorunun cevabını vermek için iki basamaklı sayıları normal çarpma işlemi ile nasıl çarptığınızı düşünebilirsiniz. Sonucunda bu işlemde de dört ayrı adım vardır. Yani çubuklar ile yaptığımız şey ile klasik çarpma işleminde yaptığımız şey temelinde aynıdır. Ancak çarpma işleminin kavranması açısından çubukları ( ya da çizgileri) kullanmak daha kolay olacaktır. Konunun pekişmesi için aşağıdaki çarpma işlemlerine de göz atabilirsiniz.
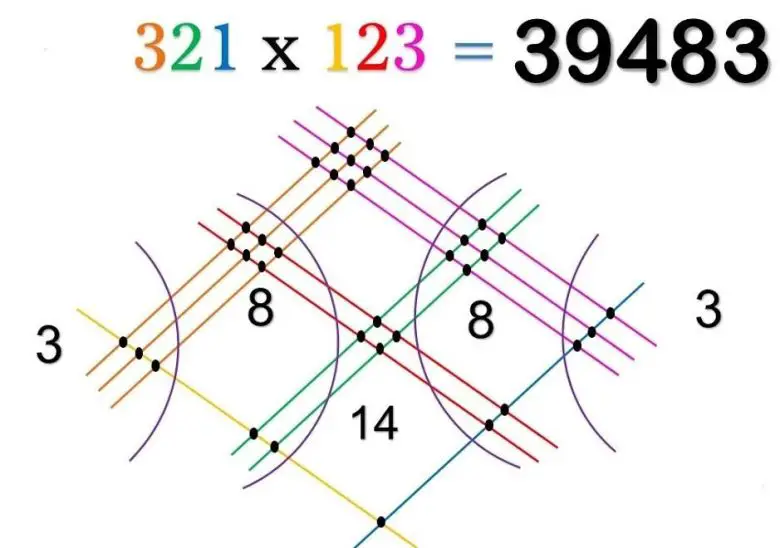
Bu görsel yöntem çocuklara çarpma işleminin temellerini öğretmek açısından oldukça değerlidir. Ancak büyük sayılarla uğraşırken pek kullanışlı değildir. Aşağıda üç basamaklı sayıların bu yöntemle nasıl çarpıldığını görüyorsunuz. Yöntemin işlemi biçimi tamamen aynıdır.
Aslında bir değil birden çok farklı çarpma yöntemi mevcuttur. Bir başkasına da bu yazımızda göz atabilirsiniz. Çarpma Yapmanın Eğlenceli İki Yolu: Rus Çiftçi Ve Antik Mısır Çarpımı. Ayrıca çarpma işlemi yapmanın en verimli yolunu öğrenmek isterseniz yazımız burada. Çarpma İşlemi Yapmak İçin En Hızlı Ve Verimli Yöntem Nedir?
Kaynaklar ve ileri okumalar
- Chinese Multiplication Method. Kaynak site: Study. Bağlantı: Chinese Multiplication Method
- It’s not magic, it’s math – how the Japanese multiplication method works. Bağlantı: Whizz.com. Kaynak site: It’s not magic, it’s math – how the Japanese multiplication method works
- Nasiru Hassan, Muhammad. (2020). Measuring Mathematics Skills: An Assessment of Chinese Sticks Method of Multiplication on Hearing Impaired Students’ Achievement in Sokoto State. Journal of Advanced Research in Dynamical and Control Systems. 12. 1463-1471. 10.5373/JARDCS/V12SP7/20202249.
- Volkov, Alexei. (2018). Chinese Counting Rods: Their History, Arithmetic Operations, and Didactic Repercussions. 10.1007/978-3-319-73396-8_7.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel