
Klasik müzik, ortaçağın başlangıcından 1900’lerin başlarına kadarki müziğin büyük bir bölümünü kapsar. 1550-1900 arasında da en canlı dönemini yaşamıştır. Bu dönemin en önemli isimlerinden biri Johann Sebastian Bach’tır. Eserleri üzerinde yorum yapan müzik tarihçileri her birinin ayrı bir zekâ ürünü olduğu konusunda hemfikirdir.

Onun kanonları aldatıcı derecede basit bir kurallar dizisinden oluşturulmuştur. Arka planındaki fikir ise son derece matematikseldir.
Müzikte Kanon Nedir?
Müzikte bir çeşit çok seslilik kuralı ile yapılmış parçalara kanon denir. 2 sesli bir kanon en az 2 kişi tarafından art arda başlanarak çalınır veya okunur. Bir kanonda önce birinci ses girer. Sabit bir süre geçtikten sonra tamamıyla aynı anahtardan onun “kopyası” girer. İkinci ses için de aynı sabit süre geçtikten sonra üçüncü ses aynı temayla girer. Böyle devam eder.
Kanonların çok daha karmaşık çeşitleri vardır. Karmaşıklığı artıran ilk adım, temanın kopyasının yalnızca zaman aralıklarıyla değil farklı perdelerle söylenmesiyle olur. Örneğin böylece birinci ses temaya Do sesiyle başlar.
Ancak ikinci ses dört nota yüksekten sol sesiyle başlayarak aynı temayı söyler. Karmaşıklığın ikinci adımı farklı seslerin hızları eşit olmadığında ortaya çıkar. Yani ikinci ses birinci sesin iki katı hızlı veya iki katı yavaş olur.
Daha bitmedi! Kanon kuruluşunda karmaşıklığın sonraki adımı temayı çevirmedir. Bach çevirmelere özellikle düşkündü, eserlerinde sıkça örneklerine rastlanmaktadır. Bunun en iyi örnekleri Müzikal Sunu’da (Musical Offering) karşımıza çıkar.
En karmaşık kanon türü de ters yönde olanlardır. Yani tema zaman içinde sondan başa doğru çalınır. Bu hilenin kullanıldığı kanon, yengecin yürüyüşünün özelliği nedeniyle yengeç kanonu diye adlandırılmaktadır.

Bach ve Yengeç Kanonu
Barok müzik özünde saray müziği idi. Dönemin Prusya kralı, Kral Büyük Friedrich tam bir müzik aşığıydı. Kral’ın onbeş kadar Silbermann piyanosu olduğu bilinmektedir. Frederick yalnızca piyanoların değil, J. S. Bach’ın da hayranıydı. Ayrıca, Frederick, sarayında akşamları oda müziği konserleri düzenlemeyi severdi.
Sonunda 1747’de bu davetlerden bir tanesine Bach’da dahil oldu. Bu ziyarette Bach Kral’dan kendisine bir Füg konusu vermesini istedi. ( Füg kanona benzer. Genellikle farklı seslerde ve farklı anahtarlarda, bazen de farklı hızlarda, baş aşağı ya da geri geri çalınan bir tema içerir.)
Kral konusunun doğaçlamadan ustaca çalınmasından hayranlık duyarak ve herhalde sanatın nereye kadar varabileceğini görmek için altı zorunlu sesli bir Füg dinlemek istediğini söyledi. Sonrasında da “Musikalisches Opfer” [Müzikal Sunu] ortaya çıktı. Müzikal Sunu’daki on kanon Bach’ın yazdığı kanonlar arasında en ince işlenmiş olanlardır.
Ama tuhaftır ki Bach bunları hiçbir zaman tamamıyla yazıya dökmemiştir. Bu kasıtlı yapılmıştır. Bunlar Kral Frederick’e bulmacalar halinde sunulmuştur. Bunun nedeni de bir tema üzerine kurulan kanonun bir başkası tarafından keşfedilmesinin o günlerin yaygın bir müzik oyunu olmasıdır. Müzikal Sunu elbette Yengeç kanonu da içeriyordu.
Yengeç kanonu müzikal bir Möbius şerididir
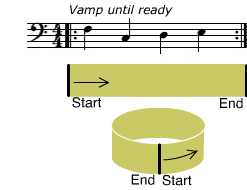
Nota diziliminin temelde iki boyutu vardır: perde ve zaman. Zaman koordinatı soldan sağa doğru ilerler (x ekseni) ve perde koordinatı ise yüksekliğe karşılık gelir ( y- ekseni). Topolojik olarak bu iki boyutlu bir şerittir. Ancak bu dizilim içinde simetri barındırırsa ortaya ilginç bir şey çıkar. Eğer bir eser, aynı nota dizisini tekrar tekrar çalıyorsa karşımıza topolojik olarak bir silindir çıkar. Bach’ın tüm kanonları bu şekilde düzenlenmiştir.
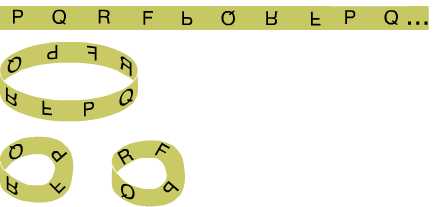
Kayma-yansıma simetrisine sahip herhangi bir periyodik metin bir Möbius şeridine uygulanabilir. Möbius şeridi, geometrik olarak uzunca bir şeridin bir ucunu 180 derece bükerek diğer ucu ile birleştirilmesiyle elde edilen yüzeydir. ( Detaylar: Möbius Şeridi Ve Klein Şişesi: Gerçeklik Algımızı Zorlayan İki Topolojik Nesne)

Yukarıda kısaca aktarmaya çalıştığımız oluşum biçimi Bach’ın yengeç kanonunda da karşımıza çıkar. Ayrıca süreci bu video da dinleyerek daha iyi kavrayabilirsiniz.
Kaynaklar ve ileri okumalar:
- Bach and the musical torus; https://plus.maths.org/
- Douglas R. Hofstadter; GÖDEL, ESCHER, BACH: bir Ebedi Gökçe Belik; ISBN 978-605-87953-0-3
- J.S. Bach – Crab Canon on a Möbius Strip; Bağlantı: https://www.youtube.com/watch?v=xUHQ2ybTejU
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel








