Deneysel bilimin verilere ihtiyacı vardır. Ancak tüm veriler rastgele değişkenliğe tabidir ve rastgele değişkenlik, verilerdeki kalıpları gizler. Bu nedenle, verilerin altında yatan gerçekler hakkında çıkarımlar yapmak için istatistiksel yöntemler kullanılır. Çoğu bilim insanı, bunun için birbiriyle yakından ilişkili iki istatistiksel yaklaşımı kullanır. Bunlar anlamlılık testi ve hipotez testidir. İlk adım ise bir sıfır hipotezi ortaya koymaktır.

Pek çok bilimsel soru basit bir evet ya da hayıra indirgenebilir. Bir şey oluyor mu, olmuyor mu? Yeni bir ilaç, tedavi etmek amacında olduğu hastalığa etki ediyor mu, yoksa hiçbir şey yapmıyor mu? Psikolojik bir müdahale sizi daha mutlu yapıyor mu yoksa hiçbir şey yapmıyor mu? Bir reklam satışları arttırıyor mu, yoksa arttırmıyor mu? Burada “hiçbir şey yapmama” senaryosuna sıfır hipotezi ya da boş hipotez denir.
Ancak içinde boş ve sıfır kelimesinin geçmesi sizi yanıltmasın. Bu hipotez çok önemlidir. Gerçekte test edilen tek hipotez budur. Sıfır hipotezi her zaman mevcut durumu belirtir: İki popülasyon arasında hiçbir fark yoktur. Hava durumu ile büyüme oranları arasında bir ilişki yoktur. Yani sıfır hipotezi destekleniyorsa olağandışı hiçbir şey olmuyor demektir.

Bilim insanları sıfır hipotezini çürütmek için bir deney yaparlar. Veri toplama yoluyla sıfır hipotezine karşı kanıt oluştururlar. Eğer kanıt yeterliyse, bir dereceye kadar olasılıkla sıfır hipotezinin doğru olmadığını söyleyebilirler. Daha sonrasında da alternatif hipotezi kabul ederler.
Alternatif hipotez, sıfır hipotezinin kabul edilmediği durumda otomatik olarak onun yerine geçecek olan hipotezdir. Yani yeni keşiflere, kararlara ve ilerlemelere yol açabilecek hipotezdir. Sıfır hipotezini reddedebilirseniz, bu alternatif hipotez için destek sağlar. Peki ama bunu nasıl yapacaksınız?

Sıfır Hipotezi Nedir Ve Nasıl Çalışır?
Bunun için hipotez testi yapmamamız gerekecektir. Buna sıfır hipotez anlamlılık testi (null hypothesis significance) denir ve ilk olarak yirminci yüzyılın başlarında, istatistiğin modern pratiğinin kurucusu olan R. A. Fisher tarafından geliştirilmiştir. Sürecin nasıl çalıştığını anlamak için basit bir örnekle ilerleyelim.
Uyku bozuklukları araştırmasında işbirliği yapan iki araştırmacı olan Dr A ve Dr B adlı iki kurgusal karakter olsun. Bir gece Dr. A elma yedikten sonra kanepesinde uyuyakalır. Ertesi sabah Dr B’nin kapısını çalar ve harika bir fikri olduğunu söyler. ” Akşamları elma yemek uykusuzluğu çare olabilir mi?” Bu basit soruyu bilimsel olarak araştırmaya değer bir şeye dönüştürmek için doktorlar aşağıdaki hipotezleri öne sürer.

- Sıfır Hipotez: Elma yemek uyku kalitesini artırmaz
- Alternatif Hipotez: Elma yemek uyku kalitesini artırır
Şimdi sırada bu hipotezi, uyku bozukluğu olan kişiler üzerinde test etme süreci vardır. Bunun için öncelikle uyku bozukluğu hastalarının rastgele iki gruba ayrılması gerekecektir. 1. Gruptaki hastalardan akşam yemeğinden sonra bir elma yemeleri istenecektir. 2. Gruptakilerden ise (“kontrol” için) elma dışında bir meyve yemeleri istenebilir. Umudunuz elma yiyen hastaların uykuya kolayca dalmasıdır.
Elma araştırmamızda her grupta yalnızca dört hasta olduğunu hayal edin. 1. Gruptaki üç hasta (%75), 2. Gruptaki iki hasta (%50) ile yemekten sonra meyve yedikten sonra daha kolay uyuduğunu bildirdi. Bu sonuçtan elma yemenin uykusuzluğu hafiflettiğini söylememiz olası olmayacaktır. Çünkü işin içine şans faktörünün karışmış olması da olasıdır.
Ancak deneyde her grupta 4.000 hasta olsaydı, o zaman bulduğumuz sonuçlara daha fazla anlam yükleyebilirdik. Bu arada verilerin teorinizle tutarlı olması yeterli değildir. Aynı şekilde teorinizin zıddıyla da, sıfır hipoteziyle de tutarsız olması gerekir.
İstatistikte p Değeri Nedir?
Sıfır hipotezinin doğru olduğunu varsaydığımız zaman, beklenen sonuçların bu hipotez altında elde edilme olasılığı p olsun. Buna p-değeri denilir. Eğer bu sayı çok küçükse, sonuçlarınızın istatistiksel olarak anlamlı olduğunu söyleyebilirsiniz. Eğer bu sayı büyükse sıfır hipotezinin bertaraf edilemediğini kabul etmeniz gerekecektir.
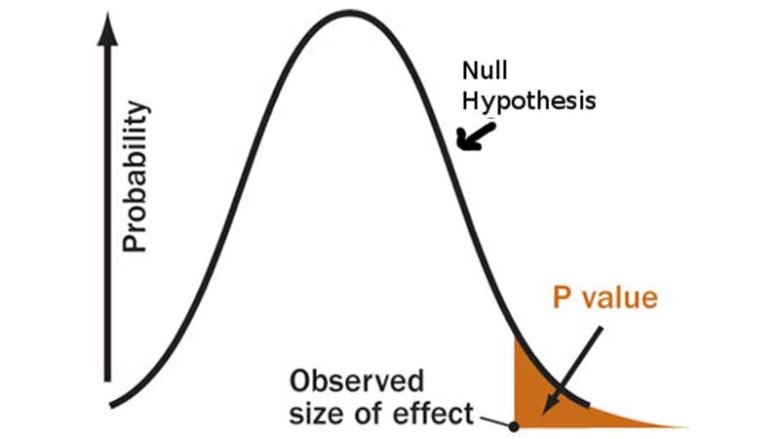
Peki ama ne kadar küçük “çok küçük”tür? Neyin anlamlı olduğu ve neyin anlamlı olmadığı arasında çizilebilecek keskin bir çizgiyi nasıl seçeceğimize dair bir kaide yoktur. Ancak Fisher’ın kendisiyle başlayan
ve şu an yaygın bir şekilde bağlı kalınan bir gelenek vardır.
Bu da, p’nin eşik değeri olarak alfa 0,05’i yani 1/20’yi kabul etmektir. Alfa, belirli bir hipotez testi için sabit anlamlılık düzeyini belirtir. Bu yanı zamanda yanlış pozitif olarak da bilinen Tip I Hata olasılığını kabul etmeye hazır olduğunuz eşiği de belirtir.
Tip 1 Hata (Hatalı Pozitif) Nedir?
Tip 1 hata, gerçek bir boş hipotezi yanlış bir şekilde reddettiğinizde oluşur. Bu hata tipine yanlış / hatalı pozitif de denir. Yeni bir ilacı test eden bir ilaç şirketini ele alalım; eğer ilaç gerçekten işe yaramıyorsa (gerçek bir sıfır hipotezi), o zaman bu boş hipotezi reddetmek ve ilacın işe yaradığını iddia etmek, özellikle de hastalara gerçekten işe yarayan bir ilaç yerine bu ilacı veriyorsanız, çok büyük sonuçlar doğurabilir. Bu nedenle de ilaç şirketi öncelikle Tip I Hata olasılığını azaltmakla ilgilenecektir.

Tip II Hata ise yanlış bir sıfır hipotezini kabul etmeniz durumunda olur. Bazen bu hata da sorunlar çıkmasına neden olur. Örneğin toksinlerin su kalitesi üzerindeki etkisini inceleyen bir araştırmayı düşünelim. Gerçekte sıfır hipotezi yanlışsa (yani, toksinlerin varlığı su kalitesini etkilerse), Tip II Hata yanlış bir sıfır hipotezinin kabul edilmesi ve hiçbir etkisinin olmadığı sonucuna varılması anlamına gelir.

Hangi İstatistiksel Analiz Daha Doğru Sonuçlar Verecektir?
Aslında bu sorunun cevabı uğraştığınız değişkenle ilgilidir. En yaygın iki değişken türü vardır. İlki sürekli değişkenlerdir. Bunlar her türlü değeri alabilir. Bir reaksiyonun tamamlanmasına kadar geçen süreyi ölçerseniz, sonuçlar 30 saniye, iki dakika 13 saniye veya üç dakika 50 saniye olabilir. İkincisi ise kategorik değişkenlerdir. Tüm sürekli değişkenler kategorik değişkenlere dönüştürülebilir. Örneğin sonuçları bir dakikadan az, bir ila üç dakika ve üç dakikadan uzun olarak kategorize edebiliriz.
Hangi değişkenlere sahip olduğunuzu öğrendikten sonra iki ana analiz türü arasında hangisinin kullanılacağına karar vermek gerekir. ANOVA (Varyans Analizi), kategorik bir değişkeni sürekli bir değişkenle karşılaştırmak için kullanılır. Doğrusal Regresyon ise iki sürekli değişkeni (örneğin zamana karşı santimetre cinsinden büyüme) karşılaştırırken kullanılır.
İstatistikler hakkında bilmeniz gereken her şey elbette bu kadar değildir. Ancak bu yazı bir başlangıç noktası olabilir. Devamında göz atmak isteyebilirsiniz. Sık Yapılan İstatistik Hataları ve Bunlardan Kaçınmanın Yolları
Kaynaklar ve ileri okumalar
- Explainer: what is a null hypothesis? Yayınlanma tarihi: 20 Kasım 2012. Kaynak site: Conversation. Bağlantı: Explainer: what is a null hypothesis?
- Null Hypothesis: What Is It and How Is It Used in Investing? Yayınlanma tarihi: 2 Kasım 2023. Kaynak site: Investopedia. Bağlantı: Null Hypothesis: What Is It and How Is It Used in Investing?
Matematiksel