Isaac Newton, cömertliğiyle tanınan bir figür değildi ve rakiplerine karşı duyduğu küçümseme adeta efsaneleşmişti. Ancak, rakibi Gottfried Leibniz’e yazdığı ve bugün Epistola Posterior olarak bilinen bir mektubunda alışılmadık bir şekilde nostaljik ve dostane bir tavır sergiler. Bu mektupta, matematiği yeni öğrenmeye başladığı öğrencilik yıllarına dair bir hikâye anlattı. Bu hikaye, binom kuvvet serilerini nasıl keşfettiğini anlatıyordu.

Her şey genç Newton’ın John Wallis’in 17. yüzyıl matematiğinde çığır açan Arithmetica Infinitorum adlı eserini okumasıyla başladı. Wallis, π sayısının değerini belirlemek için yeni ve tümevarımsal bir yöntem bulmuştu. Newton da benzer bir şey geliştirmek istedi. Çalışmalarına, x genişliğindeki bir dairesel parçanın alanı problemiyle başladı.
Bu bölge, y = √(1−x²) denklemiyle tanımlanan birim çemberin altında, x = 0 ile x arasındaki yatay eksenin üzerinde kalan kısımdı. Burada x, 0 ile 1 arasında herhangi bir değer olabiliyordu ve çemberin yarıçapı 1’di. Newton, birim çemberin alanının pi olduğunu biliyordu. Bu nedenle x = 1 olduğunda, eğrinin altındaki alanın çemberin çeyrek dilimi olduğunu ve π/4’e eşit olduğunu fark etti. Ancak x’in diğer değerleri için bu alanın nasıl hesaplanacağı bilinmiyordu.
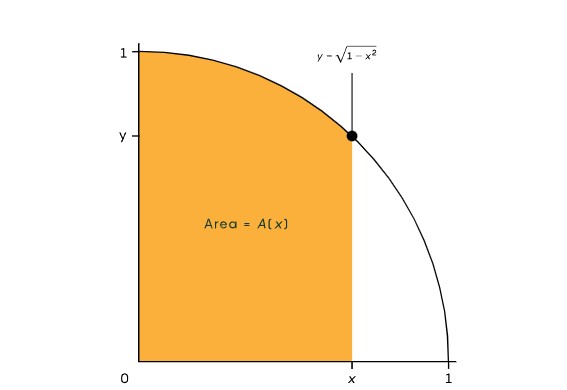
Newton, her x değeri için eğrinin altında kalan alanı hesaplamanın bir yolunu bulabilirse, pi’yi tahmin etmenin benzersiz bir yöntemine ulaşabileceğini düşündü. Bu onun başlangıçtaki büyük hedefiydi. Ancak araştırması sırasında daha büyük bir keşif yaptı. Bu keşif, matematikte çığır açan yeni bir anlayışın temelini oluşturdu.
İntegralle Alan Hesabından Binom Açılımına
Newton’un ilk adımı benzetme yoluyla akıl yürütmek oldu. Dairesel parçanın alanını doğrudan hesaplamaya çalışmak yerine, benzer özelliklere sahip eğrilerle sınırlanmış alanları araştırmaya başladı. Bunun için, belirli eğrilerle sınırlanan segmentlerin alanlarını incelemeye yöneldi. Aşağıdaki eğrilerle tanımlanan benzer parçaların alanlarını inceledi:
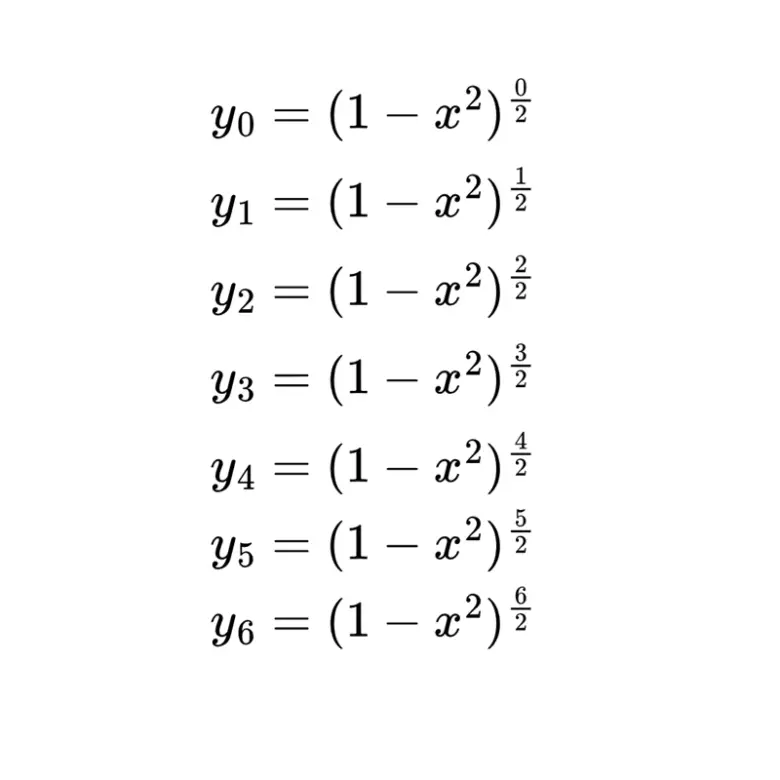
Yukarıdaki denklemlerden kuvveti tam sayı olanların (y0, y2, y4 ve y6) alanlarını hesaplamak kolaydı. Örneğin y0 ‘ın değeri 1’e eşitti çünkü kuvveti 0’dı. Ayrıca, y2, y4 ve y6 içinse integralle alanı hesaplamak mümkündü. Ancak kesirli kuvvetler içeren eğriler için böyle bir basitleştirme mümkün değildi. O dönemde, bu tür eğrilerin altındaki alanları bulmanın bilinen bir yöntemi yoktu.
Aşağıdaki listede, n bir doğal sayı olmak üzere An eğrilerin altında kalan alanı temsil etmektedir. Newton, kuvvetleri tam sayı olmayan eğri denklemlerinin alan ifadelerini tam olarak bilemediği için oralara “?” bırakmıştır. Daha sonra bu “?” olan yerleri diğer denklemlerden yola çıkarak bulmuştur. Ve böylece binom kuvvet serilerini keşfetme yolunda büyük bir adım atmıştır.
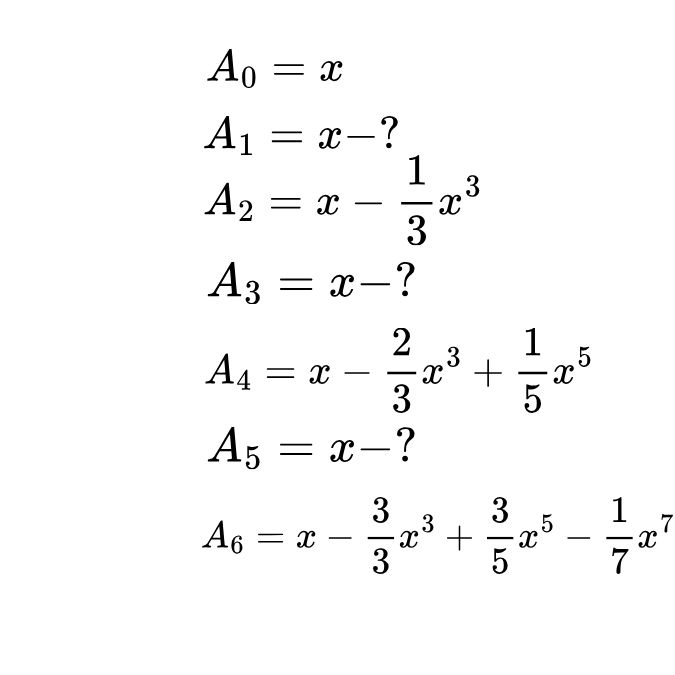
Denklemlerdeki Gizli Pascal Üçgeni
Newton’un fikri, eksik parçaları tamamlamak için, serilerde gördüğü örüntülerden yola çıkarak genelleme yapmak idi. Hemen fark ettiği bir şey vardı: Her Aₙ serisi x ile başlıyordu. Newton ayrıca, bilinmeyen terimleri doldurmak için x³ terimlerine baktı. Küçük bir cebirsel dönüşüm yaparak A₀’in bile bir kübik terim içerdiğini fark etti. Bu ifadeyi A₀ = x – (0/3)x³ şeklinde yeniden yazdı..
Leibniz’e yazdığı mektupta, x³ terimlerinin payındaki sayıların (0, 1, 2, 3, …) aritmetik bir dizi oluşturduğunu gözlemlediğini belirtti. Bu örüntünün eksik terimlerde de devam edeceğini düşündü. Buna göre A1, A3 ve A5 ‘in terimleri sırasıyla şu şekildeydi:
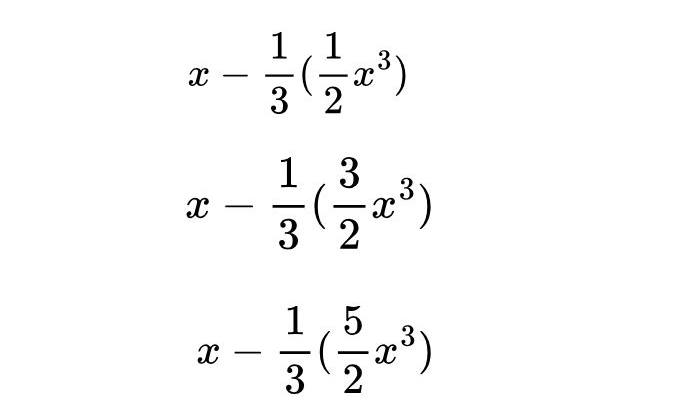
Bu, doğru yolda olduğunu gösteriyordu. Ancak daha fazla örüntüye ihtiyacı vardı. Newton, denklemlerdeki paydaların her zaman artan tek sayılar içerdiğini fark etti. Örneğin, A₆ ifadesinde paydalarda 1, 3, 5 ve 7 sayıları yer alıyordu. Aynı örüntü A₄ ve A₂ için de geçerliydi.
Geriye kalan tek şey paylarda bir örüntü bulmaktı. Newton, A₂, A₄ ve A₆ ifadelerini incelediğinde ilginç bir düzen fark etti. A₂ = x – (1/3)x³ ifadesinde, pay da 1; A₄ = x – (2/3)x³ + (1/5)x⁵ ifadesinde, paylarda 1, 2, 1 sayılarını gördü. A₆ = x – (3/3)x³ + (3/5)x⁵ – (1/7)x⁷ ifadesinde ise 1, 3, 3, 1 dizilimini fark etti. Bu sayı dizileri, Pascal üçgenini anımsatıyordu.
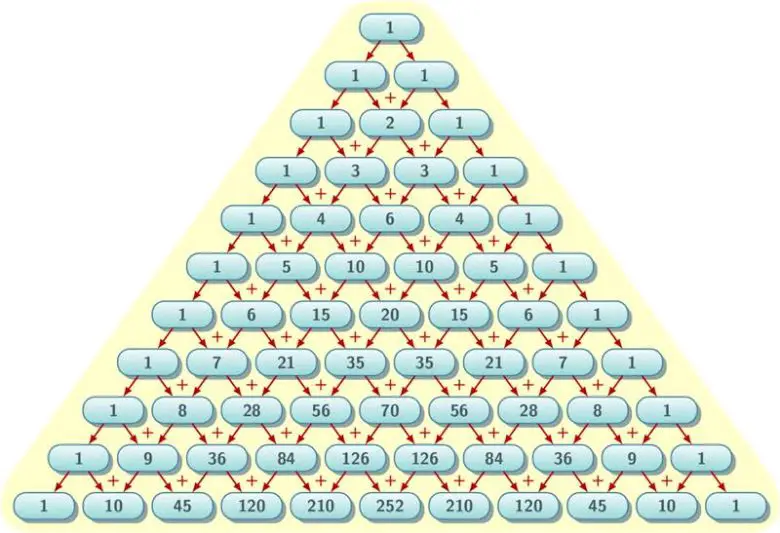
Bu örüntüyü keşfettikten sonra, Newton artık A₂, A₄, A₆ gibi A değerlerini kolayca yazacak bir yönteme sahipti. Ancak asıl hedefi, bir genelleme yapmaktı. Bunun için Pascal üçgenini genişletmesi gerekiyordu. Bu sıra dışı yaklaşımla, üçgenin genelleştirilmiş binom katsayılarını türetti.

Binom Kuvvet Serilerinin Keşfi
Newton, Leibniz’e yazdığı mektubunda, tümevarımsal yöntemiyle keşfettiği örüntüleri özetledi. “Paydaların 1, 3, 5, 7 vb. şeklinde aritmetik bir ilerleme içinde olduğunu düşünmeye başladım. Böylece yalnızca paylardaki sayısal katsayıların araştırılması gerektiği ortaya çıktı. Ancak, dönüşümlü olarak verilen alanlarda, bu katsayılar 11 sayısının kuvvetlerinin rakamlarıydı…
Yani, ilk olarak ‘1’; ardından ‘1, 1’; üçüncü sırada ‘1, 2, 1’; dördüncü sırada ‘1, 3, 3, 1’; beşinci sırada ‘1, 4, 6, 4, 1’ vb. ve böylece serideki geri kalan rakamların ilk iki verilen rakamdan nasıl türetilebileceğini araştırmaya başladım. İkinci rakam yerine m koyduğumda, geri kalanların bu serinin terimlerinin sürekli çarpımı ile üretileceğini buldum.” Newton ara satırlardaki değerler için m satır numarası olmak üzere aşağıdaki formülü üretmişti.
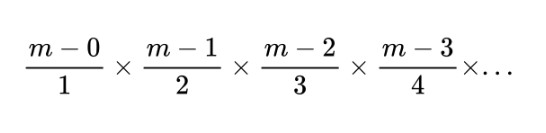
Yukarıdaki formülde m=1/2 değerini verdiğimizde -1/8, 1/16, -5/128,… şeklinde ilerleyen değerler elde ederiz. Bunlar A1 denklemindeki binom katsayılarıdır. Dolayısıyla A1 aşağıdaki gibi devam eden bir denklemdir. Bu şekilde devam eden Newton en sonunda x=1 değeri için π/4 sonucunu veren bir toplam elde etti. Genç fizikçi, hem binom kuvvet serilerini keşfetmiş hem de bu yöntemiyle π sayısının ilk 15 basamağını hesaplamıştı.
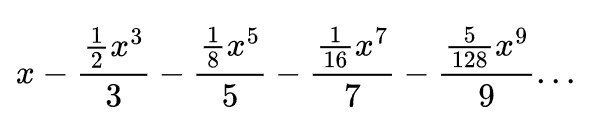
Bu keşif, karmaşık eğrilerin altındaki alanları, sonsuz seriler yardımıyla hesaplamanın kapısını araladı. Newton’un bu yöntemi, daha sonra türev ve integral hesaplarının temelini oluşturan matematiksel analiz tekniklerine ilham verdi.
Sonuç Olarak
Fakat Newton‘ın hıyarcıklı veba salgınından ötürü karantinada olduğu bu süreçte böylesi bir keşif yapmasından çıkarabileceğimiz dersler var. Eğer bir problem ilk etapta gözünüze çok zor göründüyse probleme başka bir açıdan bakmayı denemeliyiz. Zira Newton’ın yaptığı da buydu. π için çıktığı yolculukta problemi başka bir alana taşıyıp çözüm üretmeye çalışmıştı.
Kaynaklar ve İleri Okumalar
- The Discovery That Transformed Pi ; Video Bağlantısı: https://youtu.be/gMlf1ELvRzc
- How Isaac Newton Discovered the Binomial Power Series ; Bağlantı: How Isaac Newton Discovered the Binomial Power Series | Quanta Magazine ; Yayınlanma tarihi: 31 Ağustos 2022
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





