Aritmetik mi, geometrik mi, yoksa harmonik ortalama mı?. Hangi ortalamanın işe yarayacağını bilmek, soruyu gerçekten anlamakla başlar.

Elinizde bazı sayılar var ve bu sayıların tipik değerini temsil edecek tek bir sayı bulmak istiyorsunuz. Biraz matematik ya da istatistik biliyorsanız, aklınıza ortalama, daha doğrusu aritmetik ortalama gelir. Sayıları toplar, elinizdeki sayıların adedine bölersiniz. Oldukça basit.
Ama okulda bir noktada geometrik ortalama diye bir şey öğrenmişsinizdir. İstatistikçilerin “merkezi eğilim ölçüsü” dediği bu ortalama türü, aritmetik ortalamaya benzer; tek farkı, toplama yerine çarpma, bölme yerine kök alma kullanılmasıdır. İki sayının geometrik ortalamasını bulmak için onları çarpar ve sonucun karekökünü alırsınız. Aşağıda geometrik ortalamanın formülünü görebilirsiniz.
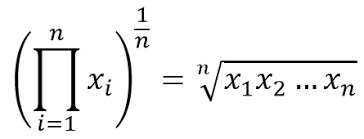
Aritmetik ortalama, toplama işlemiyle ilgili durumlarda kullanılır. Eşit ağırlıklı sayıları özetlemek için uygundur. Örneğin, bir grup öğrencinin notlarının ya da bir işçinin günlük üretim miktarının ortalamasını almak istiyorsanız, aritmetik ortalama doğru seçimdir.
Geometrik ortalama, çarpma ilişkisi olan durumlarda işe yarayacaktır. Oranlar, büyüme hızları ya da faiz gibi yüzdelik değişimleri ifade eden verilerde en doğru sonucu verir. Verilerinizin çoğu küçük, yalnızca birkaçı aşırı büyükse, tıpkı gelir dağılımında olduğu gibi, geometrik ortalama aritmetik ortalamadan ya da ortancadan çok daha anlamlı bir temsil sağlar.
Peki Ya Harmonik Ortalama?

Detaylara geçmeden önce bir soru soralım. Güneşli bir hafta sonu sabahında Çokgezenler ailesi, günübirlik bir gezi için Şile’ye gitmeye karar verdi. Ne var ki aynı fikre sahip olan birçok kişiyle birlikte onları yoğun bir trafik bekliyordu.
Gidişte ortalama hızları saatte 30 kilometre kadardı. Gün bitip akşam dönüş yoluna çıktıklarında trafik daha da sıkışmıştı. Bu kez ortalama hızları saatte 20 kilometreye düştü. Peki, yolculuk boyunca ortalama hızları neydi?
Ortalama hızı bulmak için çoğu kişinin yaptığı gibi iki hızı toplayıp ikiye bölmek, 25 sonucunu verir. Ancak bu basit görünen cevap yanlıştır. Gerçek ortalama hız 24 km/saattir.
Ortalama hız, toplam yolun toplam süreye bölünmesiyle bulunur. Burada mesafeyi bilmiyoruz ama bu önemli değil; çünkü sonuç, hangi mesafeyi seçersek seçelim aynı çıkacaktır.
Diyelim ki Çokgezenler ailesinin evi ile Şile arası 60 kilometre. Gidiş hızı saatte 30 kilometre olduğuna göre yol 60/30 = 2 saatte tamamlanır. Dönüşte hız 20 kilometreye düşerse, bu kez süre 60/20 = 3 saat olur. Böylece toplam 120 kilometrelik yol 5 saatte alınmıştır. 120’yi 5’e böldüğümüzde ortalama hızın 24 km/sa olduğunu buluruz.
Bu sonucun yoldan bağımsız olduğunu söylemiştik; o hâlde genel bir çözüm yapalım. Evin Şile’ye uzaklığı x kilometre olsun. Gidiş süresi x/30, dönüş süresi x/20 olur. Toplam süre x/30 + x/20 = 50x/600 saat eder. Toplam yol 2x’tir. Yolu zamana böldüğümüzde x’ler birbirini götürür ve sonuç yine 24 km/sa çıkar.
Ortalama hız hesabı harmonik ortalama ile ilişkilidir. Harmonik ortalama, özellikle oranlar ve hızlarla çalışırken işe yarayan bir ortalama türüdür. Aritmetik ortalama, sayıları toplayıp bunları adetlerine böler. Geometrik ortalama ise çarpımsal ilişkileri ele alır.
Harmonik ortalama ise ters oranların söz konusu olduğu durumlar için geliştirilmiştir. Bir sayı grubunun harmonik ortalamasını bulmak için şu adımlar izlenir:

- Önce her sayının tersini alın.
- Bu ters sayıların aritmetik ortalamasını bulun.
- Son olarak, elde ettiğiniz sonucun tersini alın.
Sonuç Olarak
Mühendisler ve fizikçiler, hesaplamalarında sıkça harmonik ortalamayı kullanır. Bunun nedeni, birçok fiziksel sistemde ilişkilerin ters orantılı olmasıdır. Örneğin, paralel bağlı elektrik devrelerinde toplam direnç, dirençlerin terslerinin toplamına göre belirlenir. Bu durumda aritmetik değil, harmonik ortalama işe yarar.
Aynı mantık akustikte ses frekanslarını analiz ederken veya optikte merceklerin birleşik odak uzaklıklarını hesaplarken de geçerlidir. Bu alanların ortak paydası, büyüklüklerin ters oranla birleşmesidir.
Ama harmonik ortalama sadece teknik alanlara özgü değildir. Günlük hayatta da karşımıza çıkar. Sabit mesafeleri farklı hızlarla alan bir aracın ortalama hızını hesaplarken, üretim hatlarında ortalama verimi belirlerken ya da internet bağlantısında veri aktarım hızını değerlendirirken en doğru sonuç harmonik ortalamayla elde edilir.
Bu yüzden, “ortalama” deyip geçmeden önce, sorunun yapısını iyi anlamak gerekir. Basit görünen soruların arkasında bazen daha derin bir matematik yatar.
Kaynaklar ve ileri okumalar:
- Eastaway, Robert.; Wyndham, Jeremy. Why Do Buses Come in Threes? : The Hidden Mathematics of Everyday Life
- Why is harmonic mean used for speeds, not arithmetic mean?; https://www.quora.com/
- Santos RG, Giulianotti MA, Dooley CT, Pinilla C, Appel JR, Houghten RA. Use and implications of the harmonic mean model on mixtures for basic research and drug discovery. ACS Comb Sci. 2011 May 9;13(3):337-44. doi: 10.1021/co100065a. Epub 2011 Mar 11. Erratum in: ACS Comb Sci.2011 May 9;13(3):344. PMID: 21395284; PMCID: PMC3096014.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





