Amber Heard’in güzelliği birçok kişi tarafından kabul edilir. Ancak estetik cerrah Julian De Silva, onun sadece güzel olmadığını, matematiksel olarak dünyanın en güzel yüzüne sahip olduğunu iddia ediyor. Bu iddiasını Altın Oran adı verilen matematiksel bir kavramla ilişkilendiriyor

Güzellik, yüzyıllardır sanat, felsefe ve bilim dünyasında tartışılan bir kavram olmuştur. İnsanlar estetik algıyı anlamak için birçok teori geliştirmiştir ve bunlardan biri de Altın Oran’dır. Yaklaşık 1.618 değerine sahip olan bu irrasyonel sayı, doğada, sanatta ve mimaride estetik uyumun bir ölçütü olarak kabul edilmektedir.
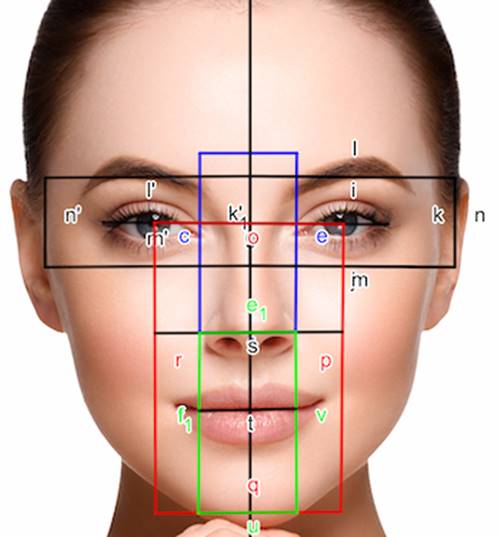
Altın Oran’ı bir güzellik ölçütü olarak savunanların başında, kozmetik cerrah Stephen R. Marquardt gelmektedir. 2002 yılında, yüz estetiğinin Altın Oran tarafından belirlendiğini iddia etmiş ve bu doğrultuda matematiksel güzellik kuralları geliştirmiştir. Marquardt, ideal yüz oranlarını temsil etmek için geometrik bir yüz maskesi tasarlamış ve bunu sinema oyuncularının ve modellerin yüz oranlarıyla karşılaştırmıştır.
Angelina Jolie, Elizabeth Taylor ve Amber Heard gibi ünlü kadınların yüzlerinin bu maskeyle büyük ölçüde örtüştüğü belirtilmiştir. Bu analizlere dayanarak Amber Heard’ün dünyanın en güzel yüzlü kadınlarından biri olduğu sonucuna varılmıştır.

Marquardt’ın iddiaları kısa sürede büyük yankı uyandırdı. Magazin dergileri, gazeteler ve güzellik içerikleri üreten platformlar bu fikri yaygınlaştırdı. Günümüzde plastik cerrahi uygulamalarında Altın Oran sıkça bir referans noktası olarak kullanılmakta ve yüz estetiği analizlerinde bu oranı temel alan çeşitli uygulamalar giderek popüler hale gelmektedir.
Ancak burada önemli bir soru ortaya çıkmaktadır. Birkaç kişinin yüzü Altın Oran’a uyduğunda, bu oran gerçekten evrensel bir güzellik ölçütü olabilir mi? Bu sorunun cevabını vermek için önce Altın Oran’ın ne olduğunu hatırlayalım
Altın Oran Nedir?
Altın Oran, irrasyonel bir sayıdır ve Yunanca φ (phi) harfi ile gösterilir. Matematiksel olarak şu formülle tanımlanır:
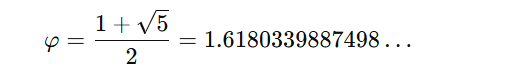
Tarih boyunca Altın Oran, güzellikle sık sık ilişkilendirilmiştir. Ancak bu iddiaların çoğu bilimsel olarak doğrulanmamıştır. İnsan vücudunda birçok farklı oran bulunur ve çoğu 1 ile 2 arasında bir değere sahiptir. Bu oranlardan bazıları tesadüfen 1.618’e yakın olabilir. Ancak bu onun evrensel bir güzellik formülü olduğu anlamına gelmez.
Ayrıca, Altın Oran irrasyonel bir sayı olduğu için tıpkı Pi (π) gibi sonsuz basamaklıdır. Bu nedenle, gerçek dünyadaki hiçbir nesne veya yüz ona tam olarak uyamaz.
Altın Oran Ve Yüz Güzelliği Arasındaki İlişki Pazarlama Stratejisidir.
Gerçek bilim, teorileri desteklemekten çok, onları çürütmeye çalışarak sağlamlıklarını test etmeyi gerektirir. Ancak Altın Oran’ın yüz güzelliği ile olan ilişkisi konusunda yapılan çalışmalar genellikle belirli bir popülasyon ile sınırlıdır. Marquardt’ın yüz maskesinin bilimsel bir standart olarak kabul edilmesi, temsil ettiği örneklemin çok dar olması nedeniyle tartışmalıdır.
Sonraki araştırmalar, bu maskenin Afrikalı, Asyalı veya Hintli bireylerin yüz hatlarını temsil etmediğini göstermiştir. Aslında, oluşturulan model büyük ölçüde Kuzeybatı Avrupalı kadınların yüz oranlarına dayanmaktadır. Bu durum, Altın Oran’ın güzelliği tanımlayan evrensel bir kriter olmadığını ve güzellik anlayışının kültürel farklılıklarla şekillendiğini ortaya koymaktadır.
Bunun ötesinde, yüz oranlarını ölçerken kulağın başlangıcı veya burnun bitiş noktası gibi kriterlerin kesin olarak belirlenmesi oldukça zordur. İnsan yüzü, milimetrik ölçümlerle matematiksel bir formüle tam olarak uydurulamayacak kadar değişkendir.
Güzellik, yalnızca simetri ve oranlarla açıklanabilecek kadar basit bir kavram değildir. Farklı kültürlerde ve farklı zaman dilimlerinde güzellik algısı değişiklik göstermektedir. Bir dönemde ince yüz hatları ideal kabul edilirken, başka bir dönemde dolgun yüz hatları cazip görülebilir. Bu da güzelliğin değişken ve öznel bir kavram olduğunu gösterir.
Güzellik İle İlgili Bazı Matematiksel Teoriler Vardır?
Güzellikle bağlantılı görünen bazı matematiksel fikirler gerçekten de var. Örneğin, çoğu insan ortalama bir yüz şeklini çekici bulma eğilimindedir. Her etnik grubun farklı güzellik idealleri olsa da, belirgin yüz özelliklerini dengelediğinizde geriye kalan, genel olarak daha kabul gören bir estetik anlayışıdır.
Büyük çeneler, orantısız kulaklar ve uzun alınlar gibi yüz hatları aşırı uçlarda olduğunda, insanlar bunları daha az çekici bulabilir. Bunun arkasında evrimsel bir neden olabilir. Eş seçiminde, sağlıklı ve güçlü genetik yapıyı temsil eden yüz hatlarını tercih etmeye yatkınız. Bu nedenle, olağandışı yüz şekillerinden bilinçaltında kaçınma eğiliminde olmamız şaşırtıcı değildir.

Bu noktada yüz simetrisi de güzellikle ilişkilendirilmektedir. Yapılan araştırmalar, simetrik yüzlerin daha çekici bulunduğunu gösteriyor. Ancak burada ilginç bir çelişki var: İnsan yüzü asla mükemmel derecede simetrik değildir. Çocukluk boyunca geçirilen hastalıklar, çevresel etkiler ve genetik faktörler yüz gelişiminde küçük farklılıklara neden olur.
Bir gözün diğerinden birkaç milimetre daha yüksek olması, bir burun deliğinin diğerinden biraz daha büyük olması gibi detaylar genellikle dikkat çekmez. Ancak bilinçaltımız, bu asimetrik detayları algılar ve kişinin genel sağlık durumu hakkında ipuçları çıkarır. Evrimsel açıdan bakıldığında, daha simetrik yüzlerin daha sağlıklı ve genetik olarak daha güçlü bireyleri temsil ettiği düşünülerek tercih ediliyor olabilir.
Sonuç Olarak
Altın Oran’ın yüz güzelliğini belirlediğine dair hiçbir bilimsel kanıt yoktur. Matematikte böyle sihirli bir sayının var olduğu ve estetik algımızı doğrudan şekillendirdiği fikri temelsizdir. Bunu aslında kendinizde deneyebilirsiniz. Aşağıda dikdörtgenlerden ilki altın orana uygun çizilmiştir. Diğerlerinde ise en ve boy arasında farklı oranlar mevcuttur. Bunlardan birinin diğerlerinden daha güzel olduğunu iddia etmek olası değildir.

Sonuç olarak, Altın Oran’ın güzelliği belirleyen bir yasa olduğu fikri bilimsel bir temele dayanmamaktadır. Estetik algı, kişisel, kültürel ve biyolojik faktörlerin bir kombinasyonu olarak şekillenir ve matematiksel bir formüle indirgenemez.
Kaynaklar ve ileri okumalar
- Does Amber Heard really have the world’s most beautiful face? An expert explains why the Golden Ratio test is bogusy. Yayınlanma tarihi: 24 temmuz 2022. Bağlantı: Does Amber Heard really have the world’s most beautiful face? An expert explains why the Golden Ratio test is bogusy/
- Holland E. Marquardt’s Phi mask: pitfalls of relying on fashion models and the golden ratio to describe a beautiful face. Aesthetic Plast Surg. 2008 Mar;32(2):200-8. doi: 10.1007/s00266-007-9080-z. PMID: 18175168.
- Veerala G, Gandikota CS, Yadagiri PK, Manne R.Juvvadi SR, Farah T, Vattipelli S, Gumbelli S. Marquardt’s Facial Golden Decagon Mask and Its Fitness with South Indian Facial Traits. J Clin Diagn Res. 2016 Apr;10(4):ZC49-52. doi: 10.7860/JCDR/2016/16791.7593. Epub 2016 Apr 1. PMID: 27190951; PMCID: PMC4866249.
- Hwang K, Park CY. The Divine Proportion: Origins and Usage in Plastic Surgery. Plast Reconstr Surg Glob Open. 2021 Feb 22;9(2):e3419. doi: 10.1097/GOX.0000000000003419. PMID: 33680667; PMCID: PMC7929632.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






