Günlük hayatımızda, en kısa ve en verimli rotayı bulmak sıkça karşılaştığımız bir problemdir. Matematikçiler bu tür problemlere “Gezgin Satıcı Problemi” (Travelling Salesman Problem) adını verir.

Örneğin, sabah uyanıp gün içindeki görevlerinizi planladığınızı düşünün:
- Bankaya gitmelisiniz
- Alışveriş yapmalısınız
- Çocukları okuldan almalısınız
- Doktora uğrayıp reçetenizi yazdırmalısınız
Bu işleri yaparken benzin tüketimini minimumda tutmak için en kısa rotayı nasıl belirleyebilirsiniz? İşte Gezgin Satıcı Problemi, bu tür optimizasyon sorularına matematiksel çözümler sunmaya çalışır. Matematikte, N sayıda varış noktası olan bir gezginin izlemesi gereken olası tur sayısı şu şekilde hesaplanır. Az sayıda durak için çözüm nispeten kolaydır.
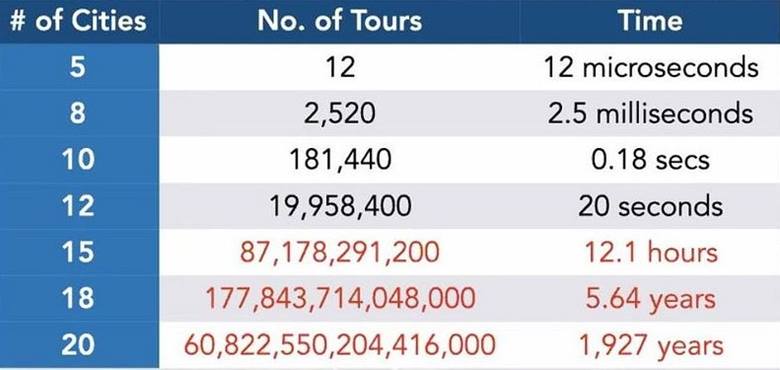
- 5 yer ziyaret etmek istiyorsanız: 12 farklı olası rota vardır.
- 10 varış noktası için: 181.400 olası yol vardır. Bir bilgisayar bunu yaklaşık bir saniyede hesaplar.
- 15 nokta için yaklaşık yarım gün,
- 20 nokta için yaklaşık 2.000 yıl,
- 25 nokta için 10 milyar yıl sürecek bir hesaplama gereklidir.
Günümüzde bilgisayarlar oldukça hızlı olsalar da, belirli bir noktadan sonra gezgin satıcı problemine çözüm bulmak imkansız hale gelir. Neyse ki, kuantum bilgisayarlar bu gibi karmaşık hesaplamaları çok daha kısa sürede gerçekleştirme potansiyeline sahiptir.
Gezgin satıcı problemi, yalnızca akademik bir matematik konusu değildir. Ulaşım planlaması, lojistik yönetimi, üretim hatları optimizasyonu, devasa veri kümeleri arasında en iyi bağlantıları bulma gibi birçok alanda gerçek dünyada uygulanmaktadır. Matematiğin soyut bir alan olduğu düşünülse de, günlük hayattaki karmaşık problemleri çözmede ne kadar büyük bir rol oynadığını gösteren en iyi örneklerden biridir.
Gezgin Satıcı Problemi Nedir?
Gezgin Satıcı Problemi bir satıcının belirli sayıda şehri yalnızca bir kez ziyaret edip başlangıç noktasına en kısa mesafede dönmesini amaçlayan bir optimizasyon problemidir. Bu problem birçok alanda kullanılsa da bazı temel zorlukları vardır.
Öncelikle, hesaplama açısından büyük bir sorun teşkil eder. Şehir sayısı arttıkça olası yolların kombinasyonu üstel olarak artar. Sonucunda bu da klasik yöntemlerle çözümü neredeyse imkânsız hale getirir. Bir diğer problem, optimum çözümü bulma güçlüğüdür. Brute-force (kaba kuvvet) yöntemiyle tüm yolları denemek mümkün olsa da, büyük ölçekli problemler için pratik değildir. Bu nedenle, yaklaşık çözümler sunan çeşitli algoritmalar geliştirilmiştir.
Bir algoritmanın bir problemi çözmesi için gereken süre, yürütmesi gereken adım sayısı ile doğrudan ilişkilidir. Örneğin, eğer bir algoritma problemi çözmek için n2 adım atıyorsa, 10 şehir için 100 adım, 20 şehir için ise 400 adım gerekecektir.
Ancak bazı algoritmaların adım sayısı çok daha hızlı artar. Örneğin, problemi çözmek için 2n adım gerektiren bir algoritma kullanırsanız, 10 şehir için 1.024 adım gerekirken, 20 şehir için bu sayı 1 milyonun üzerine çıkar. Bu tür üstel büyüme, büyük ölçekli problemlerde hesaplamayı neredeyse imkânsız hale getirir. Gezgin Satıcı Problemi, teorik bilgisayar biliminin temel konularından biri olan P ve NP problemleri ile yakından ilişkilidir.
P ve NP Problemleri Nedir?
Bir algoritmanın çalışma süresi, problemin büyüklüğüne göre değişir. n2, n3 gibi ifadeler, problemin büyüklüğü n arttıkça hesaplama süresinin makul bir şekilde büyüdüğünü gösterir. Bu tür algoritmalara polinom zamanlı algoritmalar denir ve genellikle verimli kabul edilmektedir. Peki, Gezgin Satıcı Problemi için bir polinom zamanlı algoritma var mı? Bu sorunun cevabı henüz bilinmemektedir.
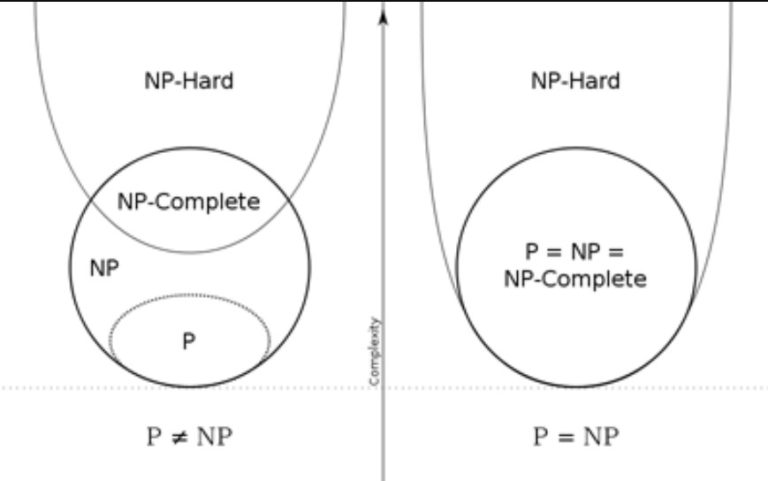
Bilgisayar bilimlerinde P ve NP problemi, karmaşıklık teorisinin en önemli konularından biridir. P sınıfı, bilgisayarların verimli bir şekilde çözebildiği problemlerdir. Örneğin, bir sayı sütununu sıralamak veya iki nokta arasındaki en kısa yolu bulmak P sınıfına girer. Bu tür problemler için algoritmalar kısa sürede çözüm üretecektir.
NP sınıfı problemler, çözümlerinin verimli bir şekilde doğrulanabildiği ancak doğrudan çözülmesinin zor olduğu problemlerdir. Bir problemin NP sınıfında olması, onun mutlaka çözülemeyecek kadar zor olduğu anlamına gelmez. Bunun yerine, eğer bir çözüm verilirse, bilgisayarın bu çözümün doğruluğunu polinom zamanda kontrol edebilmesi gerekir. Gezgin Satıcı Problemi, NP sınıfındaki problemlerin en bilinen örneklerinden biridir.

Bilgisayar bilimlerinde en büyük sorulardan biri şu şekildedir. Her NP problemi, aynı zamanda P sınıfına da mı aittir? Yani, çözümü doğrulaması kolay olan her problemi, hızlı bir şekilde çözmek mümkün mü? Günümüzde P = NP olup olmadığı bilinmemektedir. Bu sorunun çözümü, Clay Matematik Enstitüsü tarafından bir milyon dolarlık ödüle layık görülen yedi büyük matematik probleminden biridir.
Gezgin Satıcı Problemi Çözülürse Ne Olur?
Hücre biyolojisinden oyun teorisine kadar pek çok bilim dalı ve endüstri, P’ye karşı NP sorusunun yanıtını merak ediyor. Bunun temel nedeni, modern kriptografi sistemlerinin büyük ölçüde zor hesaplama problemlerine dayanmasıdır. Günümüzde şifreleme yöntemleri, yalnızca doğru gizli anahtarın bilinmesi halinde çözülecek şekilde tasarlanmıştır. Ancak P = NP eşitliğinin doğru olduğu ispatlanırsa, kredi kartı bilgileri, şifreler ve diğer dijital güvenlik sistemleri hızla çözülür hale gelir.
Bu nedenle, örneğin Gezgin Satıcı Problemi gibi klasik bir NP-zor problemi için verimli bir algoritma bulan kişi, teorik olarak en değerli şifreleme sistemlerini kıracak güce sahip olur. Bu keşif, milyonlarca dolarlık bir ödül kazandıracaktır; ancak aynı zamanda büyük bir tehlike de yaratır.

Bu tür senaryolar, bilim kurgu eserleri için de ilham kaynağı olmuştur. Örneğin, 2012 yapımı Traveling Salesman filmi, ABD ordusunun eline P = NP probleminin çözümünü sunan dört matematikçinin yaşadığı ahlaki ve bilimsel ikilemi konu alıyor.
Kaynaklar ve İleri Okumalar:
- One-Way Salesman Finds Fast Path Home. Yayınlanma tarihi: 5 Ekim 2017; Kaynakk: Quanta magazine. Bağlantı: One-Way Salesman Finds Fast Path Home/
- The Travelling Salesman Problem. Yayınlanma tarihi: 22 Ekim 2022; kaynak: Plus Math: Bağlantı: The Travelling Salesman Problem/
- This 90-year-old math problem shows why we need quantum computers. Yayınlanma tarihi: 4 haziran 2020. kaynak site: Big Think. Bağlantı:This 90-year-old math problem shows why we need quantum computers
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





