Good Will Hunting ya da Türkçe adıyla Can Dostum filmini muhtemelen izlemişsinizdir. İzlemediyseniz filmin çarpıcı sahnelerinden birini hatırlatalım. Matt Damon’ın tarafından canlandırılan Will Hunting, MIT’de temizlikçi olarak çalışan, bir gençtir. Bir gün profesörlerden biri, ofisinin dışındaki tahtaya zorlu bir matematik problemi yazar. Will, herhangi bir üniversite eğitimi almamış olmasına rağmen bu soruyu kolayca çözer.

Profesör sonrasında daha da zor bir matematik problemi yazar. Will soruyu yine çözer. Profesör zaman içinde çözümü kimin yaptığını anlar. Filmin devamı ikisinin ilişkileri üzerine kuruludur. Bir çok kişinin bilmediği şey filmin bu sahnesinin kısmen gerçeğe dayanmasıdır. Filmin amaçları doğrultusunda bir miktar değişiklik olsa da daha sonra ünlü bir matematikçi olacak olan George Dantzig hikayenin asıl kahramanıdır.
Kısaca George Dantzig Kimdir?
George Dantzig, doğrusal programlama alanında önemli çalışmalarıyla tanınan Amerikalı bir matematikçiydi. Simpleks algoritmasını geliştirerek, optimizasyon problemlerinin çözümünde büyük bir devrim yaptı.

1936’da Maryland Üniversitesi’nden mezun oldu, 1937’de Michigan Üniversitesi’nde yüksek lisans yaptı ve 1943’te UC Berkeley’de doktorasını tamamladı. 1966’da Stanford Üniversitesi’nde akademik kariyerine devam etti.
George Dantzig, UC Berkeley’deki yüksek lisans programında Profesör Jerzy Neyman’ın öğrencisi olarak istatistik eğitimi alıyordu. Daha sonra verdiği bir röportajda, bu olayla ilgili anısını şöyle anlattı:
“”Bir gün Neyman’ın dersine geç geldim. Tahtada iki problem vardı ve bunları ödev zannettim. Not alıp eve götürdüm. Birkaç gün sonra, ödevimi geç teslim ettiğim için Neyman’dan özür diledim, çünkü sorular beklediğimden daha zordu.”
Altı hafta sonra, Neyman büyük bir heyecanla Dantzig’in evine geldi ve “Az önce makalelerinden birine giriş yazdım. Hemen yayına göndermem için oku!” dedi. Dantzig, Neyman’ın neden bahsettiğini anlayamadı. Neyman, tahtadaki iki problemin aslında o güne kadar çözülememiş ünlü istatistiksel problemler olduğunu ve ödev olmadığını açıkladığında, Dantzig büyük bir şaşkınlık yaşadı.
Daha sonra, Dantzig yüksek lisans tez konusu bulmakta zorlanıyordu. Neyman’a bu durumu anlattığında, profesör konuyu fazla önemsemeden, çözdüğü iki matematik problemini bir dosyaya koyarak tez olarak sunmasını önerdi. Böylece, George Dantzig’in kazara çözdüğü bu problemler, onun yüksek lisans tezi olarak kabul edildi.
Yıllar sonra, George Dantzig artık tanınmış bir bilgisayar bilimci ve matematikçiydi. Bir gün meslektaşı Don Knuth onu durdurup, “Hey George, geçenlerde Indiana’daydım ve bir kilisede seninle ilgili bir vaaz dinledim. Orta Amerika’daki Hristiyanlar üzerinde büyük bir etkin var, haberin var mı?” diye sordu. Meğerse, Dantzig’in hikâyesi “pozitif düşüncenin gücüne” dair bir örnek olarak anlatılmaya başlanmıştı.
Daha sonra hikayesinin abartılı bir versiyonu televizyon programlarında yer aldı. Bu abartmalara rağmen, hikâyenin ana mesajı değişmeden kaldı. George Dantzig, bu problemleri çözülemeyecek kadar zor olduğunu bilmeden çözmeye çalıştığı için, kendi sınırlarıyla kısıtlanmamıştı.
Simpleks Algoritması Nedir?
Simpleks algoritması, doğrusal programlama problemlerini çözmek için kullanılan bir optimizasyon yöntemidir. Belirli kısıtlamalar altında bir hedef fonksiyonun maksimum veya minimum değerini bulmayı amaçlar. Bu tür problemler genellikle kaynak tahsisi, maliyet minimizasyonu veya kar maksimizasyonu gibi konularla ilgilidir.

Algoritma, çok boyutlu uzayda en iyi çözümü bulana kadar sistematik olarak ilerleyen bir yöntem kullanır. Öncelikle, çözülmesi gereken problem bir doğrusal programlama modeli olarak yazılır. Bu model, bir hedef fonksiyon, karar değişkenleri ve kısıtlamalardan oluşur.
Hedef fonksiyon, maksimize veya minimize edilmek istenen değeri ifade eder. Karar değişkenleri, en iyi sonuca ulaşmak için belirlenen değişkenlerdir. Kısıtlamalar ise sistemin sınırlarını belirleyen matematiksel ifadelerdir.
Algoritma, çözüm uzayında bir başlangıç noktası seçerek başlar. Bu nokta genellikle kısıtlamaları sağlayan bir köşe noktasıdır. Simpleks algoritması, en uygun çözüme ulaşmak için belirli bir yön belirleyerek ilerler. Mevcut köşe noktasından, hedef fonksiyonu iyileştiren bir sonraki köşeye geçilir. Bu süreç, her adımda hedef fonksiyonun değerini iyileştirecek şekilde devam eder. Eğer ulaşılan köşe noktasında artık daha iyi bir çözüm bulmak mümkün değilse, algoritma durur ve bulunan nokta en iyi çözüm olarak kabul edilir.
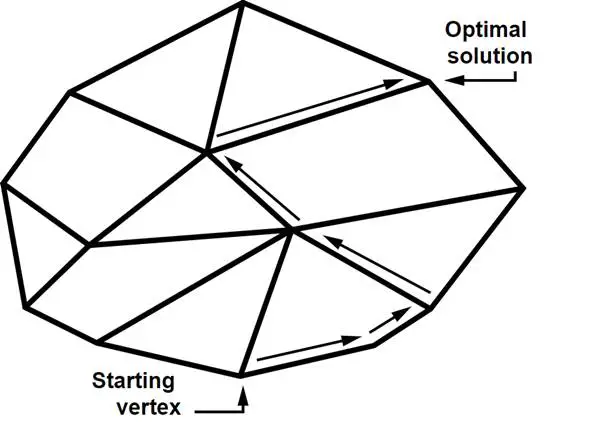
Simpleks algoritması, büyük ölçekli problemlerde hızlı çözümler üretir. Tüm köşe noktalarını tek tek denemek yerine, en iyi çözüme doğrudan yönelir. Bu algoritma, optimizasyon problemlerinde en iyi çözüme ulaşmak için sistematik bir yol sunduğu için matematik, ekonomi ve işletme gibi birçok alanda önemli bir araç haline gelmiştir. Yazının başına geri dönelim. Ya Dantzig en başında tahtadaki problemlerin çözülemez sorular olduğunu bilseydi?
Kaynaklar ve İleri Okumalar:
- The Unsolvable Math Problem; : http://www.snopes.com
- Remembering George Dantzig: The real Will Hunting; Yayınlanma tarihi:29 Mart 2019; Bağlantı: https://bigthink.com
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel