Bir dilim pizzayı bükmek neden onu yemenizi kolaylaştırır? Eğrilik ile güç arasındaki bağlantı nedir? Bu yazımız da Gauss eğrilerini öğrenelim.

Düz bir yüzeyi yuvarlak bir yüzeye ya da yuvarlak bir yüzeyi düz bir yüzeye dönüştürmek kolay değildir. İsterseniz deneyebilirsiniz. Bir portakalın etrafına bir kağıt sarmaya çalışın. Ne kadar uğraşırsanız uğraşın sonuçta kıvrımlar, kırışıklıklar olacaktır.
Şimdi de portakalın kabuğunu soyun ve düzleştirmeye çalışın. Kabuğu kesmedikçe bu da mümkün olmayacaktır. Yuvarlak ve düz yüzeylerin birbirlerine dönüşümlerini engelleyen nedir?

Gauss Eğrileri Nedir?
Aslına bakarsanız matematikçiler üç tip yüzeyden bahsederler. Bunlar her noktada sıfır Gauss eğriliği olanlar, her noktada pozitif Gauss eğriliği olanlar ve her noktada negatif Gauss eğriliği olanlar biçimindedir.
Bunun ne anlama geldiğine dair bir fikir edinmek için, bir silindirin içine bıraktığınız bir karıncanın olası hareketlerini düşünelim. Bu karınca silindirin yüzeyinde düz bir çizgi üzerinde yürüyebilir veya silindirin çevresinde tam bir çember çizerek başladığı noktaya geri dönebilir. Hatta hem dönüp hem yukarıya doğru ilerleyerek kendine spiral bir güzergah yaratabilir.
Gauss teoremi, tüm bu yolları hesaba katarak o silindirin eğriliğini ölçebileceğinizi savunur. Düz yolun eğriliği sıfırdır, eğimli yolun pozitif bir eğriliği vardır. (eğrilikler içbükey yollar için pozitif, düz yollar için sıfır ve dışbükey yollar için negatiftir.) Bu değerleri birbiri ile çarptığınızda sıfır sonucunu elde edersiniz. Daha sonra da silindirin Gauss eğriliğinin sıfır olduğu söylersiniz. Bu bir silindirin etrafına bir parça kağıt sarabileceğiniz anlamına gelir.
Bunun yerine karınca bir topun üzerinde yaşasaydı, onun için uygun düz yollar olmayacaktı. Gidebileceği tüm yollar kavislidir ve eğrilikleri pozitif sayıdır dolayısıyla çarpımları da pozitiftir. Kısacası bir kürenin Gauss eğriliği pozitiftir. İşte bu nedenle bir kağıt parçasını asla bir küre haline kesmeden getirmezsiniz.
Gauss eğrileri, bir yüzeyin nasıl manipüle edilebileceği konusunda da bize fikir verir. Yırtmadığınız sürece, bir yüzeyi büküp esnetebileceğinizi ve her yerde aynı Gauss eğriliğini koruyacağını savunur. Dolayısıyla silindiri nasıl bozarsanız bozun, Gauss eğriliği asla değişmeyecektir.
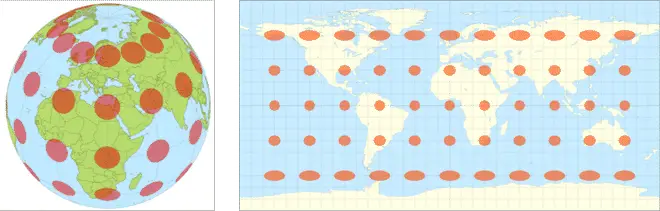
Gauss eğriliği nedeniyle bir haritayı kağıt üzerinde doğru bir şekilde çizmek imkansızdır. Görmeye alışkın olduğunuz dünya haritası, açıları doğru şekilde gösterir, ancak alanları büyük ölçüde bozar. Bir küre üzerine çizilen eşit büyüklükteki daireler, bir haritada çarpıtılmış olarak gözlemlenir.
Gauss Eğrileri ile Pizzanın Ne Alakası Var?
Büyük bir dilim pizzayı düz tutmaya çalıştıysanız bunun mümkün olmadığını deneyimlemişsinizdir. Eğer bükülmemiş bir pizza diliminin Gauss eğriliğini hesaplarsanız, sıfır elde edersiniz. (Dilimin yüzeyinde yürüyen bir karıncanın alabileceği tüm olası yollar düzdür.) Bu, o dilimi nasıl hareket ettirirseniz veya bükerseniz, sıfır değerini koruyacağı anlamına gelir.

Şimdi elinize aldığınız pizza dilimini tekrar inceleyin. Bir yandan diğer yana giden yol düz iken ( görselde kırmızı), kabuktan uca giden yolun eğimli olduğuna ( görselde siyah) dikkat edin. İlk görseldeki pizzayı malzemeleri dökmeden yemek mümkün değildir. Ancak pizza diliminin ortasından bastırarak yanları içe doğru katlarsanız düzlüğün yönünü değiştirir ve yemeye uygun hale getirirsiniz.
Eğrilik Güç Demektir
Bu iddialı başlığın anlamını basit bir deney ile gözlemleyebilirsiniz. Buzdolabınıza gidin ve bir yumurta çıkarın. Avucunuzun içine koyun, parmaklarınızı yumurtanın etrafına sarın ve sıkın. Gücünüze hayran kalacaksınız. Yumurtayı ezemeyeceksiniz.
Bunun nedeni yumurtanın yüzeyinin eğrilidir. Matematik terimleriyle ifade edildiğinde, sıfır olmayan Gauss eğriliğine sahiptir. Bu durum malzeme biliminin de özünde vardır. Oluklu mukavvaların düz mukavvalardan daha dayanıklı olması da aynı nedendendir.

Gücünü çift eğrilikten alan başka bir şekil de Pringles patates cipsidir. Bu cipsin şekli hiperbolik paraboloittir. Bu cipsin kolay parçalanmamasının sebebi itme ve çekme gücünün dengesi ile ilgilidir. İçbükey U şeklindeki kısım (siyahla gösterilmiştir) gerilirken, dışbükey kemer şeklindeki kısım sıkışır (kırmızı ile gösterilmiştir). Çift eğrilik sayesinde bu şekil, ince ancak şaşırtıcı derecede güçlü bir forma bürünür.
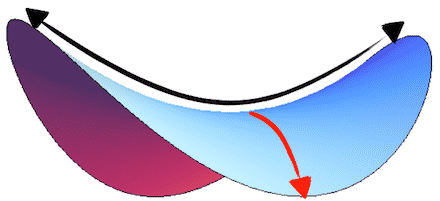
Bu Pringles şeklinin gücü, mimar ve mühendis Félix Candela tarafından iyi anlaşılmıştır. Kendisi devasa yapılar inşa etmek için hiperbolik paraboloit şekli kullanmıştır. Bu zarif yapılar son derece uzun süre dayanacak şekilde inşa edilmiştir.

Eğrilik yoluyla elde edilen güç, dünyamızı şekillendiren bir fikirdir ve köklerini geometriden alır. Bir dahaki sefere pizza sipariş ettiğinizde Gauss’u ve teoremini hatırlarsınız diye düşünüyoruz. Gauss ile adı anılan ilginç bir başka teorimi de bu yazımızdan okuyabilirsiniz: Gauss Ayakkabı Bağcığı Yöntemi İle Alan Hesaplamasını Öğrenelim!
Kaynak: How a 19th Century Math Genius Taught Us the Best Way to Hold a Pizza Slice; https://www.wired.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






