Bir algoritma, ruh eşinizi bulmak kadar kişisel bir işi de yapabilir mi? Çevrim içi flört sitelerine girdiğinizde sizi karşılayan sloganlar tam olarak bunu iddia eder: “Sizi randevularla matematik yoluyla eşleştiririz.”

Bu flört siteleri, profilleri tarayan ve insanları ilgi alanları, hoşlandıkları ve hoşlanmadıkları şeyler ile kişilik özelliklerine göre eşleştiren “eşleştirme algoritmaları” kullanır. Görünüşe bakılırsa bu işte oldukça başarılıdırlar. Hatta bazı durumlarda bizden daha iyi sonuç verdikleri bile söylenebilir.
2013’te Proceedings of the National Academy of Sciences’ta yayımlanan bir çalışma, 2005 ile 2012 arasında evlenen on dokuz bin kişiyi inceledi. İnternette tanışan çiftlerin daha mutlu olduğunu ve evliliklerini daha istikrarlı olarak tanımladıklarını ortaya koydu.
Bir algoritmanın yaratıcılarına Nobel Ödülü kazandırdığı ilk örnek de yine bir eşleştirme problemine dayanır. 1962’de matematikçiler David Gale ve Lloyd Shapley tarafından geliştirilen bu algoritma, “istikrarlı / kararlı evlilik problemi” olarak bilinen sorunu çözer.

Gale 2008’de hayatını kaybettiği için 2012’de verilen ödülü göremedi. Shapley ise ödülü, algoritmanın yalnızca aşk hayatıyla değil, sağlık hizmetlerinin ve öğrenci kontenjanlarının adil biçimde dağıtılması gibi toplumsal sorunlarla da ilgili önemini fark eden iktisatçı Alvin Roth ile paylaştı.
Kararlı Evlilik Problemi Nedir?
Gale ve Shapley’nin çözdüğü istikrarlı evlilik problemi, ilk bakışta ileri düzey bir iktisat teorisinden çok bir salon oyunu gibi görünür. Dört heteroseksüel erkek ve dört heteroseksüel kadının olduğunu hayal edin. Her biri karşı cinsten dört kişiyi tercih sırasına göre listeler. Algoritmanın görevi, bu kişileri istikrarlı evlilikler oluşturacak biçimde eşleştirmektir.

Burada amaç herkesin ilk tercihine kavuşması değildir. Esas hedef, farklı eşleşmelerde yer alan bir erkekle bir kadının, kendi eşleri yerine birbirlerini daha çok tercih edecek bir duruma düşmemesidir. Böyle bir durum ortaya çıkarsa, sistem istikrarsız hâle gelir; çünkü bu iki kişinin bir noktada mevcut eşlerini bırakıp birlikte olma olasılığı yüksektir.
Şimdi belirli bir örnek alalım ve Gale ile Shapley’nin istikrarlı bir eşleşmeyi sistematik ve algoritmik bir biçimde nasıl garanti ettiğini inceleyelim. Dört erkek, bir iskambil destesindeki papazlarla temsil edilecektir: Maça Papazı, Kupa Papazı, Karo Papazı ve Sinek Papazı. Kadınlar ise bunlara karşılık gelen kızlardır.
Her papaz ve her kız, aşağıda gösterildiği gibi kendi tercih listesini oluşturmuştur. Aşağıdaki listede papazların tercihlerini görüyorsunuz.
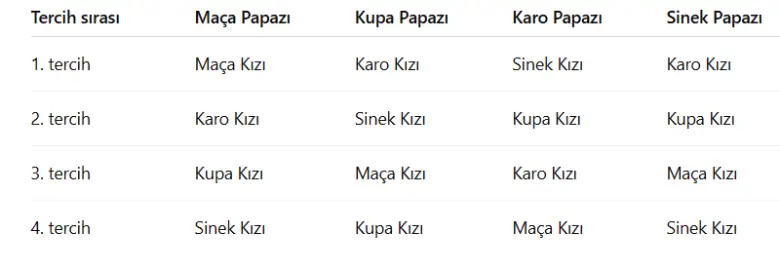
Kızların tercihleri de aşağıdaki gibi olsun.
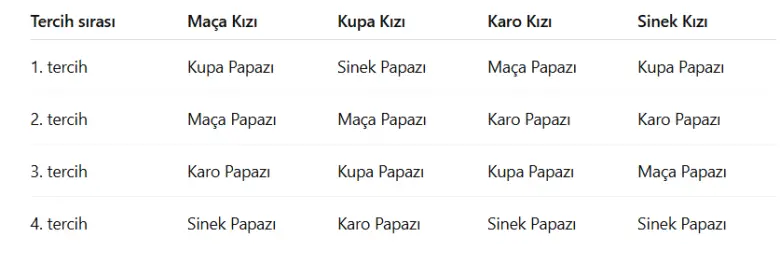
Şimdi her papazın, aynı türden kız ile eşleştirildiğini varsayalım. Bu eşleştirme istikrarsız olurdu. Önce Sinek Kızı’na bakalım. Sinek Papazı’nı tercih listesinde en sona koymuştur. Açıkçası diğer papazlardan herhangi biriyle daha mutlu olurdu.
Ardından Kupa Papazı’nın listesine bakalım. Kupa Kızı onun listesinin en altındadır. Verilen eş yerine Sinek Kızı’nı tercih ederdi. Bu durumda Sinek Kızı ile Kupa Papazı’nın birlikte kaçıp gitmesini hayal etmek zor değildir.
Peki, kimsenin eşini bırakıp başkasıyla kaçmayacağı bir eşleşmeyi nasıl kurarız? Gale ve Shapley’nin geliştirdiği yöntem tam olarak buna yanıt verir. Bu yöntem, kızların papazlara birden fazla tur boyunca teklif götürmesine dayanır. Süreç, istikrarlı bir eşleşme ortaya çıkana kadar devam eder.
Gale-Shapley Algoritması Nasıl Çalışır?
Algoritmanın ilk turunda tüm kızlar birinci tercih ettikleri papaza teklif yapar. Maça Kızı’nın ilk tercihi Kupa Papazı’dır. Kupa Kızı, Sinek Papazı’nı seçer. Karo Kızı, Maça Papazı’na teklif götürür. Sinek Kızı ise Kupa Papazı’na teklif eder.
Böylece Kupa Papazı iki teklif alır. Bu nedenle destenin gözdesi hâline gelir. Kendi tercih listesine bakar ve Sinek Kızı’nı seçer. Maça Kızı’nı ise reddeder. Sonuçta üç geçici nişan oluşur ve bir teklif reddedilmiş olur. Bu tur sonucunda tablo aşağıdaki gibidir.

Reddedilen kız, birinci tercih ettiği papazı listesinden çıkarır ve bir sonraki turda ikinci tercihine yönelir. Bu kişi Maça Papazı’dır. Ancak Maça Papazı bu aşamada iki teklif almış olur. İlki, algoritmanın ilk turunda gelen Karo Kızı’ndan gelen tekliftir. İkincisi ise Maça Kızı’ndan gelen yeni tekliftir.
Kendi tercih sırasına baktığında, Maça Kızı’nı daha çok tercih ettiğini görür. Bu nedenle, ilk turda geçici olarak nişanlandığı Karo Kızı’nı oldukça acımasızca reddeder. Sonuç aşağıdaki gibi olacaktır.

Bu da bizi üçüncü tura getirir. Her turda reddedilen kızlar, listelerindeki bir sonraki papaza teklif götürür. Papazlar ise aldıkları teklifler arasından her zaman kendileri için en iyi olanı seçer.
Üçüncü turda, reddedilmiş olan Karo Kızı bu kez Karo Papazı’na teklif yapar. Karo Papazı şimdiye kadar, kenarda kalmıştır. Karo Kızı onun tercih listesinde üst sıralarda yer almasa da, elinde daha iyi bir seçenek yoktur. Diğer üç kız, tercih ettikleri papazlar tarafından zaten kabul edilmiştir. Bu nedenle Karo Papazı teklifi kabul eder.

Bu aşamada artık reddedilen kimse kalmaz. Her papaz bir kızla eşleşmiştir ve hiçbir çift, mevcut eşlerini bırakıp birbirini tercih edecek durumda değildir. Böylece algoritma istikrarlı bir eşleşme üretmiş olur.
Sonuç olarak
Algoritmayı papazlar ve kızlarla oynanan sevimli bir salon oyunu gibi anlattık. Ancak bu yöntem bugün dünyanın dört bir yanında kullanılıyor.
Danimarka’da çocukları kreşlere yerleştirmek için uygulanıyor. Macaristan’da öğrenciler okullarla eşleştiriliyor. Çin, Almanya ve İspanya’da öğrencilerin üniversitelere yerleştirilmesinde görev alıyor. Birleşik Krallık’ta Ulusal Sağlık Sistemi, hastaları bağışlanan organlarla eşleştirmek için bu algoritmadan yararlanıyor. Bu sayede pek çok hayat kurtarılıyor.

Gale ve Shapley çalışmalarına başladıklarında, çalışmaları teorik ve soyuttu. Kararlı evlilik problemi gibi bir şey ile uğraşmaları çok kişiye anlamsız geliyordu. Ancak sonunda çalışmaları ile sayısız insanın hayatını kurtarmayı başardılar. Aynı zamanda herkesi mutlu eden bir çok eşleşme Gale ve Shapley’nin çalışmaları olmadan mümkün olamazdı.
Bugün flört sitelerinde kullanılan algoritmalar, Gale ve Shapley’nin çözdüğü bu probleme dayanır. Ancak modern durum daha karmaşıktır. Çünkü herkesin tercihleri eksik bilgiye dayanır ve zamanla değişir. İnsanlar fikirlerini sık sık gözden geçirir.
Buna rağmen algoritmaların amacı değişmez. Amaç, karşılıklı tercihlerin uzun vadede sorun yaratmayacağı eşleşmeler kurmaktır. Bunu da çoğu zaman bizden daha iyi başarırlar.
Kaynaklar ve İleri Okumalar:
- The ‘Stable Marriage Problem’ Solution Underpins Dating Apps and School Admissions. Kaynak site: Scientific Amrecican. Yayınlanma tarihiÇ 10 Ekim 2024. Bağlantı: The ‘Stable Marriage Problem’ Solution Underpins Dating Apps and School Admissions
- Monteiro, Tiago & Klimentova, Xenia & Pedroso, Joao Pedro & Viana, Ana. (2021). A comparison of matching algorithms for kidney exchange programs addressing waiting time. Central European Journal of Operations Research. 29. 10.1007/s10100-020-00680-y.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





