Mükemmel bir futbol topunu ne belirler? Oyunu oynayan ya da sadece izleyen herkes bu soruya hızla cevap verecektir. Top, kusursuz biçimde yuvarlak olmalı, yoğun fiziksel darbelerden sonra bile şeklini ve iç basıncını korumalıdır. Ancak bir sorun var. Bir topun kusursuz bir küre biçimde olması matematiksel açıdan mümkün değildir. Bu nedenle bir top tam olarak yuvarlak değildir. Sadece küreye en yakın biçimdedir.

Adidas tarafından üretilen ve “Telstar” adı verilen bu top, ilk kez 1970 Meksika Dünya Kupası’nda küresel izleyiciyle buluştu. Kısa sürede futbolun standart tasarımı hâline geldi ve bugün spor dünyasının en bilinen simgelerinden biridir.
Siyah-beyaz desenin seçilme nedeni, önceki tek renkli toplara kıyasla siyah-beyaz televizyonlarda daha görünür olmasıydı. Ancak topun temelindeki beşgen ve altıgenlerden oluşan desen Adidas’ın icadı değildi.

Aynı desen, Dorset’teki Wimborne St Giles kilisesinde Sir Anthony Ashley’nin mezarında da karşımıza çıkar. Kimi araştırmacılar bunun İngiltere’nin en eski futbol topu olabileceğini ileri sürmüştür. Şekil bazen lahana gibi sembolik yorumlara konu olsa da, mimarî olarak futbol topuna benzer bir yapı sunması bu detayın akademik dikkat çekmesine yol açmıştır
Bu şeklin izleri daha da geriye, Leonardo da Vinci’nin çizimlerine kadar uzanır. İlkenin Arşimet döneminde dahi bilindiği düşünülmektedir.

Futbol Topunun Şekli Matematikte Gizlidir
Telstar topu 32 parçadan oluşur: On ikisi siyah renkte düzenli beşgen, yirmisi ise beyaz altıgendir. Ama neden beşgen ve altıgen? Bu sorunun cevabı günümüzden ziyade geçmişte, Platonik katıların geometrisinde yatmaktadır.
Düzenli başka şekillerle bir “top” yapmaya çalışırsanız, sonuçta aerodinamiği bozacak çıkıntılar ve köşeler oluşur. Top şişirildiğinde bu hatalar kısmen düzelse de tam anlamıyla kaybolmaz. Bu klasik futbol topu biçiminin matematikte özel bir adı vardır: kesik ikosahedron. Gayriresmî adı ise “buckyball”dur. Bu ad, güçlü ve son derece verimli yapılar tasarlayan mimar Buckminster Fuller’a atfen verilmiştir.

Eğer tüm paneller aynı ve düzenli bir şekle sahip olsaydı, futbol topu üreticilerinin işi çok daha kolay olurdu. Ancak Antik Yunanlıların da bildiği gibi, bu şekilde yalnızca beş tasarım mümkündür.
Bunlar, yüzeyleri yalnızca üçgen, kare ya da beşgenlerden oluşan ve “Platonik cisimler” olarak bilinen şekillerdir. Eğer bu cisimlerin yüzeyleri yeterince esnek bir malzemeden yapılabilseydi, düz yüzlü hâlleri şişirilerek küresel bir topa dönüştürülebilirdi.
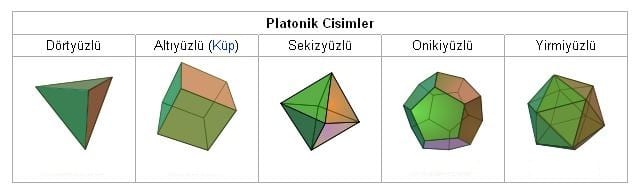
- Tetrahedron dört yüzlüdür; her yüzü eşkenar üçgendir.
- Küp, hepimizin bildiği zar şeklindedir ve altı kare yüzü vardır.
- Oktahedron, yani elmas biçimi, sekiz yüzlüdür; her yüzü eşkenar üçgendir.
- Dodekahedron on iki yüzlüdür; her yüzü düzgün beşgendir.
- İkosahedron ise yirmi yüzlüdür; her yüzü eşkenar üçgendir.
Platonik Katılar İle Yuvarlak Bir Top Yapmak Mümkün mü?
İlk üç şekil, küreye çok uzak olduğu için pratik bir top formuna uygun değildir. Şişirilip yüzeyleri kavisli hâle getirilse bile sivri köşeler ve çıkıntılar kalır. Bu da topa öngörülemez sekmeler ve uçuşlar kazandırır ki, kaleciler neredeyse küresel toplarda bile bu durumdan şikâyetçidir.
Dodekahedron ve ikosahedron küreye daha yakın formlar sunsa da hâlâ pratik kullanım için yeterince uygun değildir. Üstelik ikosahedronun bir dezavantajı vardır: Her köşede beş panelin bir araya getirilmesi gerekir ki bu, üretim hattında zahmetli bir iş olur.

Ancak ikosahedronun sorunlarını çözmenin basit bir yolu vardır: Köşeleri kesmek. Böylece her köşede artık yalnızca üç panel birleşir ve panelleri birbirine dikmek çok daha kolay hâle gelir. Ayrıca, kesilen her köşenin yerinde bir beşgen yüz oluşur.
Tüm köşeler aynı şekilde kesildiğinde toplam on iki beşgen elde edilir. Öte yandan, orijinal üçgen yüzler de küçülerek yirmi altıgen hâline gelir. Üstelik tüm kenarlar eşit uzunluktadır. Ortaya çıkan bu şekil, yani kesik ikosahedron, dünya futboluna damgasını vurmuştur. Düzenli panellerden oluşan bir katı cisim için küreye ulaşılabilecek en yakın form budur.
Futbol Topu Tasarımı Neden Değişiyor?
Adidas Telstar futbol dünyasına uzun yıllar hizmet etti, ancak futbol otoriteleri bununla yetinmedi. Teknolojiyi geliştirme çabası sürekli devam etti. Bunun ardında yalnızca oyunu daha iyi hâle getirme arzusu değil, aynı zamanda mağazaların sizi eski topunuzu bir kenara bırakıp yeni bir tane almaya ikna etme isteği de vardı. Futbol topu söz konusu olduğunda, bu çabalar özellikle onu daha küresel hâle getirmeye odaklandı.
Aslında kesik ikosahedron, beşgenleri biraz daha büyük yaparak daha küresel hâle getirilebilir. Nitelikli bazı futbol topları aslında bu yöntemle üretilmektedir. Modern bir topu dikkatle incelerseniz altıgenlerin tam anlamıyla düzenli olmadığını görebilirsiniz.

Beşgenlerle ortak kenar paylaşan altıgenlerin kenarları diğerlerinden biraz daha uzundur. Elbette bu düzensizlik bazen kalite düşüklüğünden de kaynaklanır. Özellikle ucuz plastik toplarda şekiller yalnızca yüzeye boyandığı için altıgenler tamamen rastgele görünecektir.
FIFA bir gün yeni ve dikkat çekici bir futbol topu tasarlamak isterse, başka bir seçeneği de değerlendirebilir: 62 yüzlü bir şekil. Bunun 20’si üçgen, 30’u kare, 12’si ise beşgendir. Bu yapı, kesik ikosahedrondan biraz daha küreseldir ve her farklı yüz farklı renge boyanabilir.
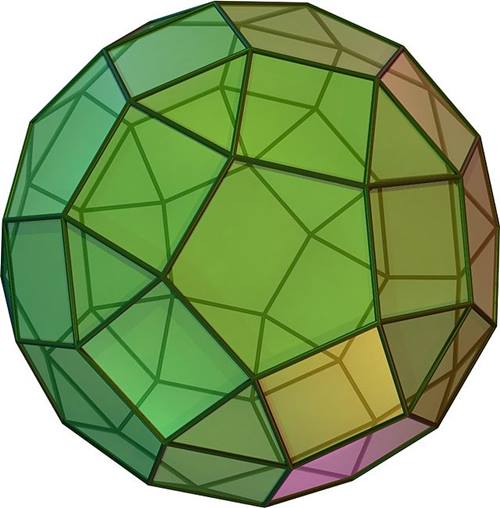
Matematikteki adı rhombicosidodecahedrondur. Dezavantajı ise oldukça uzun bir isim olmasıdır; muhtemelen devre arası yorumunun çoğu yalnızca bu ismi telaffuz etmeye giderdi. Bir diğer sorun da, bir topun fazla küresel olmasının her zaman avantajlı olmamasıdır.
Kaynaklar ve ileri okumalar:
- Kotschick, Dieter. (2006). The Topology and Combinatorics of Soccer Balls. American Scientist – AMER SCI. 94. 10.1511/2006.60.350.
- Football: aerodynamics of the perfect free kick; yayınlanma tarihi. 28 Haziran 2016; Kaynak site: Conversation. Bağlantı: Football: aerodynamics of the perfect free kick
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






Benimki bir cevap değil de teşekkür. Çok değişik ve ilginç konularda bilgileniyorum sayenizde