Matematikte, başlangıçta belirli bir problemi çözmek için tasarlanmış ancak daha sonra birçok farklı problemi çözmekte kullanılan en güzel örneklerden biri Fourier serisidir. Bu seriye adını veren ünlü matematikçi ise Joseph Fourier’dir.

“Efsanevi” demekte abartmıyoruz. Joseph Fourier, Napolyon’un Rosetta Taşı’nı bulmak için düzenlediği Mısır seferine katıldı. Isı transferi anlayışında devrim yarattı, günümüzde CT ve MRI tarama görüntülerinin oluşturulmasında kullanılan matematiksel yöntemleri geliştirdi ve sera etkisini keşfetti. Bu yüzden önce onu kısaca tanımalısınız.
Joseph Fourier Kimdir?
Fourier, 1768’de Fransa’da doğdu. Zorlu bir çocukluk geçirdi ama matematikle tanışınca hayatını değiştirdi. Bir piskopos onun yeteneğini fark edip Benediktin rahiplerinden eğitim almasını sağladı.
Gençliğinde Fransız Devrimi’ne katıldı fakat artan şiddet ortamına karşı çıkınca 1794’te bir süre hapse girdi. Serbest kalınca bir mühendislik okulunda ders vermeye başladı ve hasta meslektaşlarının yerini doldurarak fizik ve klasikler gibi konuları anlattı.
1798’de Napolyon’la Mısır’a gitti ve Fransa Bilimler Akademisi’ni örnek alan Mısır Enstitüsü’nün sekreterliğini üstlendi. İngiliz donanması ablukaya alınca savaşın devam etmesi için silah ve mühimmat üretimini organize etti. Sonunda Fransız ordusu teslim olup ülkesine döndü.

Tüm bu zorluklara rağmen önemli matematik makaleleri yayımladı. Mühendislerin her gün kullandığı denklemler ve ısı transferi katsayıları gibi kavramlar, onun bu yoğun dönemde geliştirdiği çalışmalar sayesinde hayatımıza girdi.
Fourier Serisi nedir?
Fourier’in ilk büyük katkısı, bugün “ısı denklemi” olarak bilinen kısmi diferansiyel denklemi ortaya koymasıydı. Bu denklem, bir nesnenin sıcaklığının zamana ve mekâna nasıl bağlı olduğunu açıklar. Modern gösterimde ısı denklemi şu şekildedir.

Burada k, nesnenin ısıl iletkenliğini belirleyen bir katsayıdır. Bu denklemin bir çözümü, nesnenin her noktadaki sıcaklığını her an için verir. Fourier’in en parlak buluşu, bu denklemi çözmek için sıcaklık fonksiyonunu basit fonksiyonların toplamı olarak ifade edebileceğini fark etmesiydi. Bunu, bir evi tek seferde inşa etmek yerine tuğla tuğla örmeye benzetebiliriz.
İkinci büyük buluşu ise hangi fonksiyonları seçeceğiydi. Fourier, sıcaklığı sinüs ve kosinüs fonksiyonlarının toplamı şeklinde yazmayı tercih etti. Yani sıcaklığı aşağıdaki biçimde ifade etti. Bu toplam sonsuza kadar devam eder. a0,an,bn gibi katsayılar, sistemin başlangıç koşullarına bağlıdır. İşte bu ifade, bugün Fourier serisi olarak bilinmektedir.
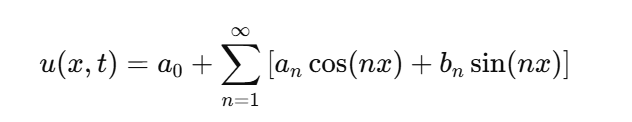
İlk bakışta, sıcaklığı sinüs ve kosinüs fonksiyonlarının toplamı şeklinde ifade etmek tuhaf bir seçim gibi gelir. Ancak Fourier’in bu tercihi, ısı denklemini çözmek için tam isabetliydi. Bu yöntem, problemi çok daha basit alt problemlere ayırmayı sağladı.
Fourier’in bu içgörüsünden kısa bir süre sonra, sinüs ve kosinüs fonksiyonlarıyla bir fonksiyonu parçalarına ayırmanın birçok başka problemi de çözebileceği anlaşıldı. Dalga hareketleri, gazların davranışı, yerçekimi problemleri, elektrostatik, elektromanyetizma ve hatta borsa hareketlerinin modellenmesi gibi pek çok alanda uygulama alanı buldu.
Fourier serisi, bir fonksiyonun sonsuz sayıda sinüs ve kosinüs fonksiyonunun toplamı şeklinde ifade edilmesini sağlar. Basitçe söylemek gerekirse, Fourier serisi üzerinde çalışılması zor periyodik fonksiyonları alır ve onları daha yönetilebilir bir grup sinüs ve kosinüs fonksiyonuna ayırır.
Fourier Serisi Ne İşe Yaradı?

Fourier, doğanın derinlemesine incelenmesini matematiksel keşiflerin en verimli kaynağı olarak görürdü. Bununla birlikte geliştirdiği matematiksel kuram pek çok farklı alanda işe yaradı. Bugün Fourier serisi yalnızca matematikte değil, fizik ve mühendislikte de temel bir rol oynamaktadır.
Dikkat çekici olan, Fourier’in denklem sisteminin katı, sıvı veya gaz fark etmeksizin birçok maddeye uygulanabilmesidir. Bu yaklaşım yalnızca ısı aktarımını anlamayı değil, elektrik akımını, difüzyon süreçlerini ve doğadaki akış hareketlerini de kavramayı dönüştürdü. Suyun gözenekli kayalardan geçişinden kılcal damarlardaki kan akışına kadar pek çok doğal sürecin matematiksel olarak modellenmesini mümkün kıldı.
Fourier serilerinin modern biçimini Joseph Fourier geliştirmemiş olsa da, trigonometrik serilerde yaptığı önemli buluş nedeniyle bu seriler onun adıyla anılır. Dalgalar yoluyla enerji aktarımıyla ilgilenen hemen her bilim dalı, Fourier’in ortaya koyduğu yöntemleri kullanır.
Örneğin, günümüzde radyologlar hastalara bakım sağlarken Fourier’in önemli bir keşfi olan Fourier dönüşümünü kullanır. Bilgisayarlı tomografi (BT) taramalarında doktorlar, hastanın vücuduna farklı açılardan X-ışını demetleri gönderir. Bu ışınların bir kısmı vücuttan geçip dedektörlere ulaşır, bir kısmı ise iç yapılar tarafından engellenir. Örneğin kemikler X-ışınlarının çoğunu engellerken akciğer dokusu çok az engeller.
Farklı açılardan yapılan çok sayıda ölçümle, her küçük doku parçasının ışını ne kadar engellediği belirlemek mümkündür. Fourier dönüşümü ve karmaşık hesaplamalar yardımıyla bu ölçümler, vücudun iç yapısının iki boyutlu kesit görüntülerine çevrilir.
Sonuç olarak
Fourier’in keşfi matematik dünyasında büyük bir hareket başlattı. Pek çok matematikçi bu fikri geliştirmek ve genelleştirmek için çalıştı. Bu süreçte Leonhard Euler’in ünlü formülüne de zarif bir yol bulundu.
Bugün Fourier serileri ve bilgisayarlardaki ayrık halleri modern teknolojinin belkemiğidir. Ses, görüntü ve veri işleme bu sayede mümkün olur. Müzik, televizyon ve video endüstrileri ise bu matematiksel temeller olmadan düşünülemez.
Fourier, yaşamı boyunca pek çok ödül elde etti. Ayrıca Fransız Bilimler Akademisi’ne seçildi. Isıya olan merakıyla ilgili ilginç söylentiler de vardı: Kat kat giyinerek saunalara girer, odalarını aşırı sıcak tutarmış. Sonunda, Mayıs 1830’da 63 yaşında bir anevrizma nedeniyle hayatını kaybetti.
Bugün adı Eyfel Kulesi’ne kazılı durumda. Ama asıl kalıcılığı, adını taşıyan Fourier serisi ve Fourier dönüşümünde yatıyor. Bu kavramlar, onun matematiğin evrenin sırlarını çözebileceğine olan inancını günümüze taşıyor.
Kaynaklar ve İleri Okumalar:
- Maths in a minute: Fourier series. Kaynak site: Plus Maths. yayınlanma tarihi: 28 Kasım 2016. Bağlantı: Maths in a minute: Fourier series/
- lan Stewart; Taming The Infinite:The Story Of Mathematics; ISBN 978-605-171-373-1
- In his 250th birthday, Joseph Fourier’s math still makes a difference. Yayınlanma tarihi: 21 Mart 2018. Kaynak site: Conversation. Bağlantı: In his 250th birthday, Joseph Fourier’s math still makes a difference
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





