Fransız Devrimi’nin karmaşası içinde, bir adamın matematiğe olan takıntısı, bugün matematik ve fiziğin temel taşlarından biri haline gelen bir hesaplama yöntemine dönüştü. Bu yöntem günümüzde, Fourier dönüşümü olarak bilinmektedir.

Bir müzik parçasını dinlerken, kulaklarımız karmaşık bir hesaplama yapar. Flütün tiz sesi, kemanın orta tonları ve kontrbasın derin uğultusu havada farklı frekanslarda basınç dalgaları oluşturur.
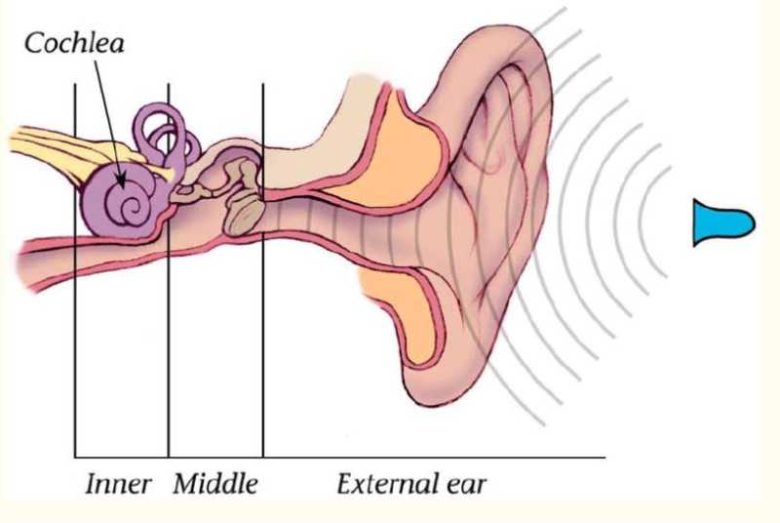
Bu birleşik ses dalgası kulak kanalından geçip spiral şekilli kokleaya ulaştığında, farklı boylardaki tüy hücreleri çeşitli frekanslara tepki verir ve bu karmaşık sinyali temel ses bileşenlerine ayırır. Ancak matematikçileri bu süreci anlaması ve denklemlere dönüştürmesi 19. yüzyılı buldu.
1800’lerin başında Fransız matematikçi Jean-Baptiste Joseph Fourier, herhangi bir fonksiyonu temel frekanslara ayırmanın bir yolunu buldu. Bu frekansları yeniden bir araya getirerek, orijinal fonksiyonu eksiksiz biçimde geri elde etmek de mümkündü.
Bugün Fourier dönüşümü olarak bilinen bu yöntem, devrimin savunucusu Fourier’in matematikte de köklü bir dönüşüm başlatmasını sağladı. Fourier dönüşümünden, fonksiyonların bileşenlerini inceleyen harmonik analiz adlı bir matematik alanı doğdu.
Kısa sürede matematikçiler, bu alan ile sayı teorisi, diferansiyel denklemler ve kuantum mekaniği gibi birçok disiplin arasında derin bağlantılar keşfetti. Günümüzde Fourier dönüşümünü bilgisayarlarımızda da görüyoruz. Dosya sıkıştırmadan ses iyileştirmeye kadar pek çok işlemde bu yöntem devreye giriyor.
Fourier Dönüşümü Nedir?
Fourier, 1768’de Fransız Devrimi öncesindeki çalkantılı dönemde doğdu. On yaşında ailesini kaybetti ve Auxerre’deki bir manastır okulunda eğitim aldı. Yıllarca yaşamını dine mi yoksa matematiğe mi adayacağını sorguladı. Sonunda dinî eğitimi bıraktı ve öğretmenlik yapmaya başladı. Bu sırada devrimci hareketlere destek verdi.

1794’te, devrime aykırı görüşler dile getirdiği gerekçesiyle yetkililer onu tutukladı ve hapse gönderdi. Giyotin sırasını beklerken, Terör Dönemi sona erdi. Böylece 1795’te yeniden matematik öğretmeye başladı. Kısa süre sonra Napolyon Bonapart onu bilim danışmanı olarak Mısır seferine dahil etti.
Mısır’da antik eserleri araştırırken, bir yandan da ısı iletiminin matematiksel yapısını anlamaya çalıştı. Bu çalışmalar, Fourier dönüşümüne giden süreci başlattı.
Fourier, bir metal çubuğun bir ucunu ısıttığımızda, ısının zamanla tüm çubuğa yayıldığını gözlemledi. Bu yayılımı, farklı frekanslara sahip basit dalgaların toplamı olarak modellemeyi önerdi. Çubuk soğudukça, bu dalgalar enerjilerini kaybeder, zayıflar ve yok olur.
İlk olarak yüksek frekanslı, hızlı titreşen dalgalar kaybolur; daha sonra düşük frekanslı olanlar da silinir. Bu süreç, bir senfoninin sona erişine benzer: önce ince sesler susar, ardından derin tonlar da yavaşça yok olur.
Fourier bu düşünceyi 1807’de Paris Enstitüsü’nde sundu. Ancak döneminin önde gelen matematikçilerinden Joseph-Louis Lagrange, çalışmayı duyduğunda, “Bu imkânsız!” diyerek tepkisini gösterdi.

Dönemin matematikçileri, sıcaklığın ani değiştiği durumların matematikle açıklanamayacağını düşünüyordu. Fourier ise sonsuz sayıda basit eğri kullanarak bu geçişleri tanımlayabileceğimizi savundu. Bugün onun haklı olduğunu biliyoruz.
Fourier Dönüşümleri Nasıl Gerçekleşir?
Fourier dönüşümünü yapmak, bir parfümü koklayıp içindeki notaları ayırt etmeye ya da karmaşık bir caz akorunu duyup hangi notalardan oluştuğunu çıkarmaya benzer.
Matematiksel olarak Fourier dönüşümü bir fonksiyondur. Karmaşık görünen bir fonksiyonu alır ve onu oluşturan frekansları verir. Bu frekanslara karşılık gelen basit sinüs ve kosinüs dalgalarını topladığınızda, baştaki fonksiyonu yeniden elde edersiniz.
Bunu gerçekleştirmek için Fourier dönüşümü, tüm olası frekansları tarar ve her birinin orijinal fonksiyona ne kadar katkı sağladığını hesaplar. Böylece karmaşık bir yapıyı, basit frekans bileşenlerine ayırır. Şimdi bunu basit bir örnekle görelim. Diyelim ki elimizde şöyle bir fonksiyon var:
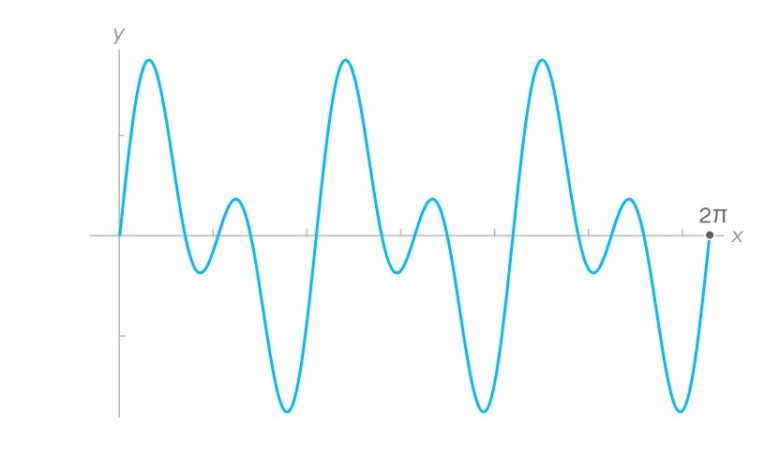
Fourier dönüşümü, her frekansın orijinal fonksiyona ne kadar katkı sağladığını anlamak için dalgaları birbiriyle çarpar. Bu işlem, belirli bir frekansın sinyalle ne kadar örtüştüğünü ortaya koyar. Örneğin, elimizdeki fonksiyonu frekansı 3 olan bir sinüs dalgasıyla çarparsak, şu olur.
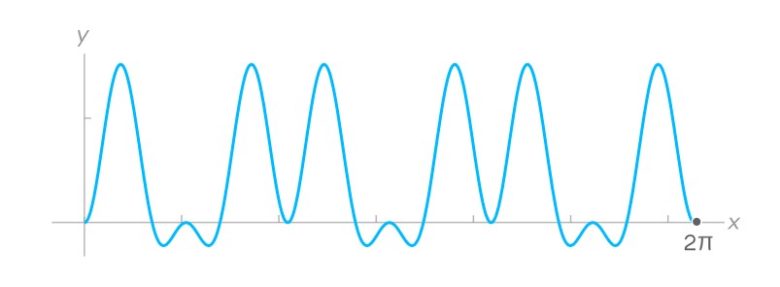
Bu çarpımın sonucu büyükse, bu frekans sinyalin içinde güçlü bir şekilde yer alıyor demektir. Küçükse, katkısı zayıftır. Bu çarpımda birçok büyük tepe noktası var. Bu da frekansın orijinal fonksiyonda güçlü bir şekilde yer aldığını gösteriyor.
Şimdi sırada 5 var. Bakalım bu frekans sinyalin içinde yer alıyor mu. Orijinal fonksiyonu, frekansı 5 olan bir sinüs dalgasıyla çarptığımızda sonuç şöyle görünüyor:
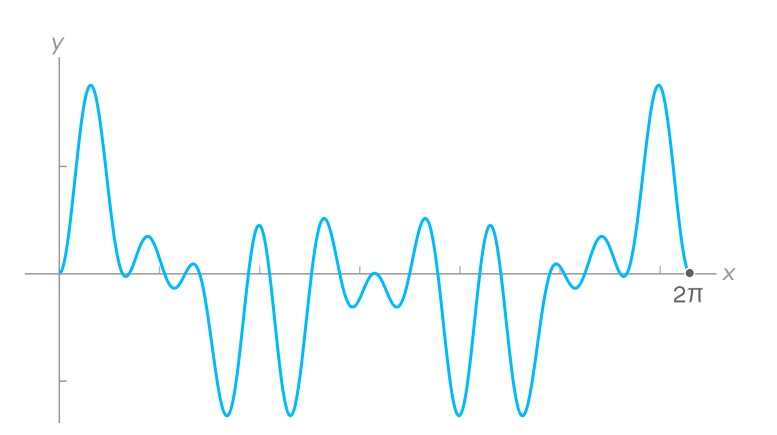
Yeni çarpımda bazı yüksek tepeler olsa da derin çukurlar da var. Grafik genel olarak sıfır civarında dengeleniyor. Bu da frekans 5’in orijinal fonksiyona katkı yapmadığını gösteriyor.
Fourier dönüşümü bu işlemi tüm olası frekanslar için yapar. Her frekansı, orijinal fonksiyonla hem sinüs hem de kosinüs dalgalarıyla çarpar. Bu sayede Fourier dönüşümü, karmaşık görünen bir fonksiyonu yalnızca birkaç sayıya indirger. Bu özelliği, onu matematikçilerin önemli araçlarından biri yapar. Bir problemle baş edemediklerinde, onu dönüştürmeyi denerler.
Eğer orijinal fonksiyon keskin bir kenara sahipse Fourier dönüşümü, bu kenarı en iyi şekilde yakalamak için sonsuz sayıda frekans üretir. Bu sonsuz frekans dizisine Fourier serisi denir. Bugün Fourier serisi fonksiyon analizinde vazgeçilmez bir araçtır.
Fourier Dönüşümleri Elektronik Cihazlarda Nasıl Çalışır?
Fourier dönüşümü, yalnızca tek boyutlu sinyallerde değil, daha yüksek boyutlu nesnelerde, örneğin görüntülerde de çalışır. Gri tonlu bir görüntüyü, her pikselin parlaklık seviyesini belirten iki boyutlu bir fonksiyon gibi düşünebiliriz. Fourier dönüşümü bu fonksiyonu, iki boyutlu frekanslara ayırır.
Bu frekanslara karşılık gelen sinüs ve kosinüs dalgaları, farklı yönlere hizalı çizgili desenler oluşturur. Bu desenler bir araya getirilerek her türlü görüntü yeniden oluşturulabilir.
Örneğin, 8×8 boyutunda bir görüntü, aşağıdaki 64 temel parçanın bir kombinasyonuyla inşa edilebilir. Sıkıştırma algoritmaları, insan gözü için çok fark edilmeyen yüksek frekanslı bilgileri kaldırarak görüntüyü kayda değer ölçüde küçültür. JPEG formatı, işte bu prensiple karmaşık görüntüleri çok daha az veriyle saklar.

1960’larda matematikçiler James Cooley ve John Tukey, Fourier dönüşümünü çok daha hızlı yapabilen bir algoritma geliştirdi. Hızlı Fourier dönüşümü (Fast Fourier Transform – FFT) adı ile bilinen bu buluş, sinyal işleme gerektiren neredeyse her alanda Fourier dönüşümünün kullanılmasını mümkün kıldı.
Bugün gelgitleri incelemekten kütleçekim dalgalarını tespit etmeye, radar ve MR teknolojisinden ses dosyalarındaki gürültüyü azaltmaya kadar sayısız alanda Fourier dönüşümü kullanılıyor. Kuantum mekaniğinde belirsizlik ilkesinin matematiksel temelini bile Fourier dönüşümü oluşturuyor.
Sonuç Olarak
Fourier dönüşümünün etkisi sadece uygulamalı alanlarla sınırlı değil. Saf matematikte de köklü bir yer edindi. Hem Fourier dönüşümünü hem de onun tersini inceleyen harmonik analiz, dalgaları ve fonksiyonları anlamak için güçlü bir araç haline geldi. Dahası, matematikçiler bu alanın sayı teorisiyle beklenmedik bağlantılar kurduğunu keşfetti. Sonucunda gerçekten de basit bir buluş dünyamızı kökten değiştirdi.
Kaynaklar ve ileri okumalar:
- Fourier transforms of images; yayınlanma tarihi: 7 Nisan 2017; Bağlantı: https://plus.maths.org/
- What Is the Fourier Transform? Yayınlanma tarihi: 3 Temmuz 2025. Kaynak site: Quanta magazine. Bağlantı: What Is the Fourier Transform?
Matematiksel





