Günümüzde bir biçimde Fibonacci sayılarını ve elbette bu sayıların meşhur altın oranla olan bağlantısını duymuş olmalısınız. Aslında Lucas sayıları, Fibonacci sayılarına benzer birçok özelliğe sahiptir.

Leonardo Fibonacci bu sayılar için ‘Fibonacci serisi’ veya ‘Fibonacci sayıları’ terimini kullanmamıştı. Zaten kendisinin asıl adı da Leonardo Bigollo Pisano idi. ‘Bonaccio’nun oğlu’ anlamına gelen ‘Fibonacci’ lakabı kendisine daha sonra takılmıştı. Diziye adını veren on dokuzuncu yüzyıl Fransız matematikçisi François Édouard Anatole Lucas (1842–1891) oldu.
Kendisi hayranı olduğu bu diziye sadece adını vermekle kalmadı. Aynı zamanda bu dizinin rakamları ile oynayarak başka diziler de elde etti. Matematiği popülerleştirme çabasında olan ve sayılar ile oynamayı seven Édouard Anatole Lucas, bu sayılarda küçük bir değişiklik yaparak Lucas sayılarını ortaya attı.

Lucas Sayılarının Fibonacci Sayıları İle İlgisi Nedir?
Fibonacci dizinin bir kısmı 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… biçimindedir. Bu sayıları oluşturan kural başlangıçta aldığımız iki adet bir sayısının dışında, diğer her sayının önceki iki sayının toplamından oluşmasıdır.
Bu sayılar günümüzde genelde tavşanlar ile ilişkilendirilse de aslında Leonardo Fibonacci, hiç bir zaman biyoloji ile ilgilenmek gibi bir amaca sahip olmamıştı. Verdiği tavşanlar aslında sadece bir örnekti. Temelinde bu sayıların onun ilgisini çekmesinin nedeni, ardışık terimleri birbirine böldüğümüz zaman sonucun phi sayısına yani altın orana giderek yaklaşmasıydı.
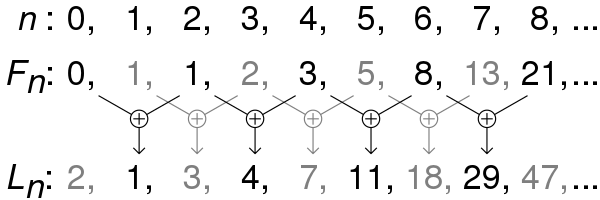
Ancal Lucas sayılarının küçük bir başlangıç farkı vardı. Başlangıcı 1,1 biçiminde değil; 2,1 biçiminde idi. Sonraki sayılar aynı Fibonacci sayılarında olduğu gibi toplama yoluyla bulunmaktaydı. Bu durumda Lucas sayıları 2, 1, 3, 4, 7, 11, 18, 29, 47… biçiminde olur.
Lucas sayıları, Fibonacci sayılarına benzer birçok özelliğe sahiptir. Bunun sonucunda da Lucas sayıları genellikle Fibonacci Sayıları için çeşitli formüllerde bulunur. Ayrıca, Lucas sayıları için birçok formüle bakarsanız, Fibonacci serisinin de orada olduğunu görürsünüz. Aşağıda ardışık Lucas sayılarının oranlarını görüyorsunuz. Fark etmiş olacağınız gibi bu oranlar da giderek phi sayısına yaklaşıyor.

İşin Arka Planında Neler Olup Bitiyor?
Aslında, bir sonrakini elde etmek için en son iki değer toplanarak oluşturulan her dizi için ve hangi iki pozitif değerle başlarsak başlayalım, sonunda oranı Phi=1.6180339.. sayısına yaklaşan terimlere sahip oluruz. Bunun için küçük bir deneme yapalım.
Birinden herhangi iki sayı seçmesini isteyin (küçükten başlamak en iyisidir, çünkü sayılar çok hızlı büyürler). Diyelim ki 4 ve 3’ü seçtiler. Birini diğerinin altına yazmalarını isteyin. Daha sonra da bu sayıları birbirileri ile toplayarak diğer sayıları elde etsinler. 4 ve 3 için sonuç şu ilk 10 sayı şöyle olacaktır: 4, 3, 7, 10, 17, 27, 44, 71, 115, 186.
Beş saniyeden daha kısa bir sürede bu 10 sayıyı toplayabilir misiniz? Evet yapabilirsiniz! Bunun için yapmanız gereken dizideki 7. sayıyı 11 ile çarpmak. Yani 44 x 11 = 484 bu 10 sayının toplamıdır. Bunun nedenini anlamak için aşağıdaki çizelgeye göz atınız.

Tabloda da fark etmiş olacağınız gibi toplamımız 55x+88y biçimindedir. Bu ise 7. satırdaki toplamın yani 5x+8y’nin tam olarak 11 katıdır. Bu nedenle bu satırdaki sayıyı 11 ile çarpmak bize her zaman genel toplamı verecektir.
Şimdi a, b, c, d biçiminde pozitif sayıları a/b < c/d biçiminde yazdığımızı düşünelim. Şimdi kötü bir kesir toplaması yapalım. Yani pay ile payı, payda ile de paydayı toplayalım. Elde ettiğimiz bu yeni kesir her zaman ilk iki kesrin arasında bir yerlerde olacaktır. (İnanmayanlar deneme yapabilirler.)
Bu durumda 10. satırdaki sayıyı 9. satırdaki sayıya böldüğümüz zaman aslında sonucumuz aşağıdaki gibi olacaktır. Bu nedenle, bölüm tahmin edildiği gibi 1.61 rakamlarıyla başlamalıdır. Kısacası ardışık terimlerin toplanması ile elde ettiğiniz tüm sayılar bir biçimde sayıların doğası gereği Fibonacci sayıları ile ilişkili olacaktır.
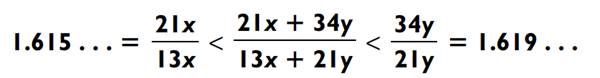
Bu yazıda sizlere kısaca Lucas sayılarını tanıtmaya çalıştık. Bu sayılar ile ilgili daha fazla bilgiye kaynaklarımız aracılığı ile erişebilirsiniz. Ayrıca göz atmak isterseniz: Fibonacci Dizisinden Sıkıldıysanız N-bonacci Dizisi İle Tanışın!
Kaynaklar ve ileri okumalar:
- Lucas Numbers – Numberphile; yayınlanma tarihi: 22 Eylül 2014; Bağlantı: https://www.youtube.com
- Lucas number; https://en.wikipedia.org/
- François Édouard Anatole Lucas; Bağlantı: https://mathshistory.st-andrews.ac.uk/
- Johnny Ball; Wonders Beyond Numbers: A Brief History of All Things Mathematical; Yayıncı: Bloomsbury Sigma (5 Ekim 2017) ISBN: 1472939999
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel