Antik çağın büyük bir bölümünde, dünyanın şekli hakkında düşünen insanlar genellikle geniş düz bir düzlemde yaşadıklarını varsaydılar. Bu, binlerce yıl boyunca makul bir inançtı. Aradan geçen bin yıllar boyunca gezegenimiz, galaksimiz ve evrenimiz hakkında birçok sır keşfettik. Ancak temel bir soru cevapsız kalmaya devam ediyor. İçinde yaşadığımız evrenin şekli nasıldır?

Evrenin şekli söz konusu olduğunda aynı hatayı yapmak kolaydır. Bize sonsuz ve eğri değilmiş gibi gözükecektir. Hatta evren çok geniş olduğu için bir şekli olmadığını bile düşünebilirsiniz. Ancak gökbilimcilerin gözlemleyebileceği bir şekle sahiptir.
Karl Schwarzschild, fikirlerinin gerçek önemini görecek kadar uzun yaşayamamış bir dahiydi. 1916 yılında yalnızca 42 yaşındayken öldü. Yıldızların, gökadaların ve kütleçekimin incelenmesinde büyük keşiflere imza attı, bugün evrenimizde çok sayıda bulunan kara deliklerin kesin tanımlamasını yaptı ve Einstein’ın görelilik kuramının sınanması için yapılan tüm hassas deneylerin önünü açtı.

Evrenin Şekli İle İlgili Olası Üç Durum
Schwarzschild tüm bunlardan önce evreninin yeni bir resmini çizdi. 1900 yılında Heidelberg’de Alman Gökbilim Derneğinin toplantısında yaptığı sunumda, evrenin geometrisinin Öklid’in bize öğrettiği gibi düz olmadığını söyledi.
Evrenin şekli, ilk önce on sekizinci yüzyılın başlarında Johannes Lambert ve matematikçi Giovanni Saccheri tarafından önerilen, daha sonra da Riemann, Gauss, Bolyai ve Lobaçevski tarafından geliştirilen Öklid dışı geometrilerdeki gibi eğri olabileceği düşüncesini ortaya attı. Günümüzde evrenin üç olası geometriden birine sahip olduğunu biliyoruz. Pozitif eğriliğe sahip küresel geometri, sıfır eğriliğe sahip Öklid geometrisi veya negatif eğriliğe sahip hiperbolik geometri.
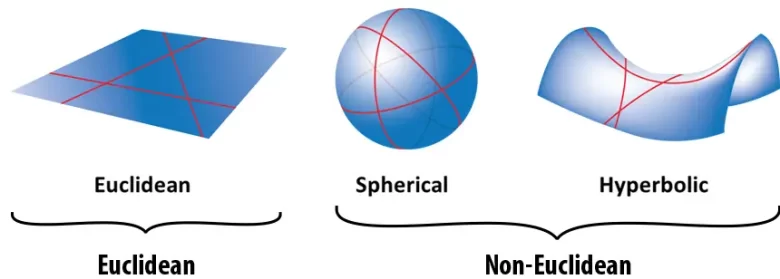
Bu üç geometrinin çok farklı özellikleri vardır. Örneğin, Öklid geometrisinde bir üçgenin açılarının toplamının 180 derece olduğunu hatırlayın. Küresel geometride durum böyle değildir. Bir küre üzerine üç nokta yerleştirilirse, aralarındaki açılar 180 dereceden fazla olur. Hiperbolik geometride, açılarının toplamının 180 dereceden kesinlikle küçük bir pozitif sayı olduğu üçgenler oluşturulabilir.
Şu anda sahip olduğumuz tüm teknolojiyi kullanarak uzayda görebildiğimiz en uzak nokta 46 milyar ışık yılı uzaklıkta. Buna gözlemlenebilir evren diyoruz. Bunun ötesinde ne olduğunu bilmiyoruz. Bu nedenle Evrenin şekli hakkında fikir sahibi olmak için bir kere daha denklemlere göz atmamız gerekiyor.
Galileo Galilei ve Isaac Newton, uzayın Öklidyen bir yapı olduğu varsayımı üzerine modern fiziği kurdular. Ancak Albert Einstein’ın genel görelilik denklemleri, karmaşık kavisli formlara sahip olabilen bir evreni tanımlıyordu. Genel Görelilik’in en önemli öngörülerinden biri, kütlenin uzayın eğrilmesine neden olduğu ve bu eğri uzayda hareket eden nesnelerin yollarının, sanki üzerlerine bir kuvvet etki etmiş gibi, sapması sonucuydu.
Uzayın kendisi eğriyse, evrenin geometrisi için üç genel olasılık vardır. Bu olasılıkların her biri evrendeki kütle miktarına (ve dolayısıyla toplam kütle çekimi gücüne) bağlıdır ve her biri evren için farklı bir geçmiş ve gelecek anlamına gelir.
Evrenin Şekli Bir Küre Gibi Kapalı mıdır?
İlk olasılık, maddenin yoğunluğunun (birim hacim başına ortalama madde miktarı) çok yüksek olmasıdır. Bu durumda evren bir top şeklinde kıvrılacaktır. Bu 3 boyutlu küreyi hayal etmek zordur. Ancak matematiksel olarak kolayca tanımlayabiliriz. Küresel geometride düz çizgiler dairelerdir. Kenarları büyük daire parçalarından oluşan bir üçgen çizerseniz, açılarının toplamının 180 dereceden fazla olduğunu göreceksiniz.

Uzay pozitif eğriliğe sahipse, evrenin şu anki genişlemesini durdurmak için fazlasıyla yeterli kütle vardır. Bu durumda genişleme sonunda duracak ve bir daralmaya dönüşecektir. Bu nedenle, gelecekte bir noktada galaksiler birbirlerinden uzaklaşmayı bırakacak ve evren kendi üzerine çökerken birbirlerine yaklaşmaya başlayacaklardır. Buna kapalı evren denir.
Evrenimiz Hiperbolik Bir Şekle Sahip Olabilir mi?
Diğer bir olasılık da, maddenin yoğunluğunun çok düşük olmasıdır. Bu durumda da Evren’in eğriliği negatif olacaktır. Bu durumda Evren”in biçimi aşağıda da gördüğünüz gibi bir eyere benzemelidir. Bu şekil üzerinde üçgenin iç açılarının toplamı 180 dereceden azdır. Hiperbolik geometri, muhtemelen size hayali bir matematiksel yapı gibi gelmiştir. Ancak Einstein görelilik teorisini geliştirdiğinde, hiperbolik geometri simetrilerinin, teorisini formüle etmek için tam olarak ihtiyaç duyduğu şey olduğuna karar vermişti.

Eğer uzay bu şekildeyse ve negatif eğriliğe sahipse, evrenin genişlemesini durduracak yeterli kütle yoktur. Böyle bir durumda, evrenin sınırı yoktur ve sonsuza kadar genişleyecektir. Buna açık evren denir.
Evren Düz Bir Şekle mi Sahiptir?
Evren sıfır eğriliğe sahipse, geometrisi okulda öğrendiğimiz sıradan 3 boyutlu uzaydır. Bu durumda üçgenlerin açıları toplamı tam olarak 180 derecedir. Uzayın eğriliği yoksa (yani düz ise), genişlemenin durmasına neden olacak kadar kütle vardır. Ancak bu sonsuz bir zaman diliminden sonra gerçekleşir.

Evren sıfır eğriliğe sahipse, geometrisi okulda öğrendiğimiz sıradan 3 boyutlu uzaydır.
Dolayısıyla, evrenin sınırları yoktur ve sonsuza kadar genişler. Genişleme hızı sonsuz bir zaman diliminden sonra kademeli olarak sıfıra yaklaşır. Buna düz evren veya Öklid evreni denir.
Evrenin geometrisi sıklıkla, evrenin gerçek yoğunluğunun, genişlemenin durması için gereken kritik yoğunluğa oranı olarak tanımlanan “yoğunluk parametresi” cinsinden ifade edilir. Dolayısıyla, evren düz ise (sadece onu kapatacak miktarda kütle içeriyorsa) yoğunluk parametresi tam olarak 1’dir. Evren negatif eğrilikle açıksa yoğunluk parametresi 0 ile 1 arasında yer alır ve evren pozitif eğrilikle kapalıysa yoğunluk parametresi 1’den büyüktür.

Kozmik mikrodalga arka plan (Büyük Patlama’dan arta kalan radyasyon) gözlemleri, Evren’in gerçekten düz olduğunu veya en azından neredeyse düz olduğunu gösteriyor. Geçtiğimiz birkaç on yılda, bilim insanları kozmik mikrodalga arka plan ışımasını incelediler. Evrende sıcak ve soğuk noktaların eşlendiği daire çiftlerini araştırdılar. Neredeyse hiç eğrilik bulamadılar. Araştırmacılar, %0,2’lik bir hata payıyla evrenin düz olduğunu buldular.
Sonuç olarak
Mevcut teorik inanç evrenin düz olduğudur. Ancak çok küçük bir olasılıkla olsa da başka bir evren biçiminin de hala olası olduğunu hatırlamak gereklidir.
Kaynaklar ve ileri okumalar
- The shape and fate of the Universe. Yayınlanma tarihi: 18 Aralık 2020; Kaynak site: Plus Math. Bağlantı: The shape and fate of the Universe./
- Shape of the universe: could it be curved, not flat?. Yayınlanma tarihi: 13 Kasım 2019. Kaynak site: Conversation. Bağlantı: Shape of the universe: could it be curved, not flat?
- Constraints on the curvature of the Universe and dynamical dark energy from the full-shape and BAO data. Anton Chudaykin, Konstantin Dolgikh, and Mikhail M. Ivanov; Phys. Rev. D 103, 023507 – Published 5 January 2021;https://journals.aps.org/
Matematiksel