Tam olarak 243 yıl boyunca çözümünün mümkün olmadığı düşünülen Euler’in 36 Subay Problemi biraz ilginç bir biçimde çözülmüş olabilir.

1779’da İsviçreli matematikçi Leonhard Euler, bir soru sordu. “Bir savaşta altı alaydan oluşan bir ordunun komutanısınız. Bu alayların her birinde, her biri altı farklı rütbeye sahip altı subay var. Yani 36 tane subay var. Bu subayları 6×6’lık bir ızgaraya yerleştirmeniz gerekiyor. Her satırında ve sütununda her alaydan ve her rütbeden sadece bir subay olacak biçimde yerleştirmek mümkün müdür?”
Bu bulmaca 36 Subay problemi olarak ünlendi. Bulmaca, beş rütbe ve beş alay veya yedi rütbe ve yedi alay için kolayca çözülebilmektedir. Ancak 36 subay için bir çözüm aradıktan sonra Euler, “böyle bir düzenlemenin imkansız olduğu, ancak bunu kesin bir şekilde gösteremeyeceği” sonucuna varmıştır.

Bir yüzyıldan fazla bir süre sonra, Fransız matematikçi Gaston Tarry, gerçekten de, Euler’in 36 subayını 6’ya 6’lık bir kareye yerleştirmenin bir yolu olmadığını kanıtladı. 1960’da matematikçiler bilgisayarlardan destek alarak, 6 hariç ikiden büyük herhangi bir sayıda alay ve sıra için çözümün mümkün olduğunu kanıtladı.
Sihirli Kareler Nedir?
Aslında benzer bulmacalar 2000 yıldan fazla bir süredir insanları büyüledi. Yukarıdaki problemi daha iyi anlamak için öncelikle sihirli kareleri anımsamanız gerekiyor. Sihirli kare, içinde 1’den n’e kadar sayıların yazılı olduğu nxn boyutlarında bir karedir. Ancak bu sayılar öyle yazılmışlardır ki her satır, sütun ve köşegenin toplamı aynı sayıya eşittir.

Bir değil bir çok özel sihirli kare vardır. Bunlardan biri de Sudoku’nun gerçek ataları olan Latin kareleridir. Latin kareleri, sayı, harf veya sembollerle dolu ızgaralardır. Ancak aynı satır veya sütunda bir sembol iki kez olmaz.
Örneğin elinizde 1,2 ve 3 rakamları olsun. Sizin bunları rakamların her biri her satır ve her sütunda birer kez olacak biçimde 3×3 lük bir ızgaraya yerleştirelim. Aşağıdaki dizilim olasılıklardan bir tanesi. Aslında tam 12 tane farklı kare yapabilirsiniz.
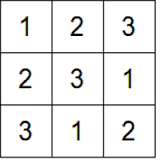
Bu örneği genişleterek istediğiniz dereceden Latin kare oluşturabilirsiniz. Bir Latin kare oluştururken illa sayı kullanmanız gerekmez. Bazen Latin kareleri birleştirmek gerekir. Bu tür karelere Greko-Latin kareler denir. Aynı zamanda Euler kareleri de denir. 36 subay problemi bir 6×6’lık bir Greko-Latin karedir.

36 Subay Problemi Nasıl Çözüldü?
Euler’in klasik probleminde, her subayın belli bir alayı ve rütbesi vardır. Ancak Euler böyle bir 6×6 karenin var olmadığını düşünürken, oyun yakın zamanda değişti. Bir makalede bir grup kuantum fizikçisi, Euler kriterlerini karşılayacak şekilde 36 subayı düzenlemenin mümkün olduğunu gösterdi. Ancak bunun için bu Latin kare bulmacasının kuantum versiyonlarını geliştirmeleri gerekti.
Ancak kuantum dünyasında bir subay, aynı anda birden fazla alayı veya rütbeyi işgal edebilir. Polonya’daki Jagiellonian Üniversitesi’nden araştırmacı Adam Burchardt, ızgarayı kuantum subaylarla doldurmanın çözümü mümkün kıldığını kanıtladı.

Günlük yaşamda, nesneleri ya “ayrı” ya da “bağlantılı” olarak düşünürüz. Aralarında bir kilometre bulunan iki top ayrıdır. Bir ip parçasıyla birleştirilmiş iki top ise birbirine bağlıdır. Ancak kimi durumlarda iki nesne hem ayrı hem de bağlantılı olabilir. Bu da bizi kuantum dolanıklık fikrine götürür.
İki nesne “dolanık” olduğunda, aralarında fiziksel bir bağlantı yoktur – ancak ayrı da değillerdir. Bu nesnelerden biri için bir ölçüm yaparsanız, ikinci nesnenin ne yaptığını, ona bakmadan önce bile bilme şansınız olur. İki nesne, onları birbirine bağlayan hiçbir şey olmamasına rağmen tek bir sistem oluşturur.
Kuantum dolanıklığının arka planındaki fikir süperpozisyondur. Süperpozisyon, parçacıkların aynı anda birden fazla durumda var olduğu fikridir. Bir ölçüm yapıldığında, parçacık süperpozisyondaki durumlardan birini seçmiş gibi olur.
Kuantum Latin karelerinin girişleri de kuantum süperpozisyonlarında olabilen kuantum durumlarıdır. Matematiksel olarak, bir kuantum durumu bir ok gibi uzunluğu ve yönü olan bir vektörle gösterilir. Bir süperpozisyon, birden fazla vektörün birleştirilmesiyle oluşan oktur. Bir Latin karesinin her satırı ve sütunundaki sembollerin tekrarlanmaması gerekliliğine benzer şekilde, bir kuantum Latin karesinin her satırı veya sütunundaki kuantum durumları birbirine dik vektörlere karşılık gelmelidir.
Sonuç olarak
Araştırmacılar çalışmalarında bir algoritma uyguladılar. Algoritma, kaba kuvvetle bir Rubik Küpü çözmeye biraz benziyordu. Algoritmayı tekrar tekrar tekrarladıklarında, bulmaca dizisi gerçek bir çözüme giderek daha da yaklaşıyordu. Sonunda, araştırmacılar deseni görebilecekleri ve kalan birkaç girişi elle doldurabilecekleri bir noktaya ulaştılar. Sonucunda Euler’in bir anlamda yanıldığı ortaya çıktı; ancak 18. yüzyılda kuantum subaylarının var olma ihtimalini bilemezdi.
Kaynaklar ve ileri okumalar için:
- The 36 officers problem; Kaynak site: Plus math. Yayınlanma tarihi: 5 Ağustos 2026. Bağlantı: The 36 officers problem
- Euler’s 243-Year-Old ‘Impossible’ Puzzle Gets a Quantum Solution; yayınlanma tarihi: 10 Ocak 2022; Kaynak site: Quanta Magazine. Bağlantı: Euler’s 243-Year-Old ‘Impossible’ Puzzle Gets a Quantum Solution/
- Centuries-old ‘impossible’ math problem cracked using the strange physics of Schrödinger’s cat; Kaynak site: Live Science. Yayınlanma zamanı: 20 Ocak 2022; Bağlantı: Centuries-old ‘impossible’ math problem cracked using the strange physics of Schrödinger’s cat;/
- Bose RC, Shrikhande SS, Parker ET. Further Results on the Construction of Mutually Orthogonal Latin Squares and the Falsity of Euler’s Conjecture. Canadian Journal of Mathematics. 1960;12:189-203. doi:10.4153/CJM-1960-016-5
- Rather, Suhail Ahmad & Burchardt, Adam & Bruzda, Wojciech & Rajchel-Mieldzioć, Grzegorz & Lakshminarayan, Arul & Zyczkowski, Karol. (2022). Thirty-six Entangled Officers of Euler: Quantum Solution to a Classically Impossible Problem. Physical Review Letters. 128. 10.1103/PhysRevLett.128.080507.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





