Günlük hayatta binler, milyonlar, milyarlar,… gibi sayılar bize büyük gibi gelse de matematik açısından bu sayılar fazla da büyük sayılmaz. Gerçekten büyük bir sayı ile tanışmak istiyorsanız Graham Sayısını bilmelisiniz. Ronal Graham’ın adıyla anılan, bu sayı büyüklüğünden dolayı 1980 yılında Guinness Rekorlar Kitabına girmeye hak kazanmıştır.

İyi bilinen bir büyük sayı googoldür. 1 googol 10100 anlamına gelmektedir. Bunu 1 sayısının sonunda 100 tane sıfır gibi de düşünebilirsiniz. Hatta daha da büyüğünü merak ederseniz googolplex yani 10googol sayısını da sizlere söyleyebiliriz.
Googolplex sayısının ne kadar büyük olduğunu bir örnekle görelim. Ortalama bir kitap hayal edelim. Bu kitabın 400 sayfası, her sayfasında 50 satırı ve de her satırında 50 tane sıfır rakamı olsun. Bu kitapta tam olarak 106 tane sıfır rakamı vardır. Yani googolplex sayısını yazmamız için bu kitaptan 1094 tane gereklidir.
Ancak matematikçiler Googolplex sayısından daha büyük sayıları da tanımladılar. Bunlardan en ünlüsü Graham sayısıdır. Bu sayımız, ister yıl Evrenin yaşından çok daha büyüktür. Graham’ın sayısı, 1078 ile 1082 arasında olduğu düşünülen gözlemlenebilir Evrendeki atom sayısından da daha büyüktür. Ancak işin ilginç tarafı bu sayı sonludur, aynı zamanda bir tam sayıdır ve akıllara durgunluk verecek kadar büyük olmasına rağmen 3’e bölünebildiğini ve 7 ile bittiğini biliyoruz.

Graham Sayısı Nedir?
Graham sayısı aynı zamanda Ramsey teorisinde bir üst sınır olarak da tanımlanmıştır. İngiliz matematikçi ve filozof Frank Plumpton Ramsey’in (1903-1930) adını taşıyan Ramsey teorisi, sistemlerde düzen ve örüntü bulmakla ilgilenir.

Büyük sayılar her zaman Ramsey teorisinin bir parçası olmuştur, ancak 1971’de matematikçi Ronald Graham, kendisinden önceki her şeyi gölgede bırakan bir sayı buldu. Ancak bu sayıyı bilimsel gösterimle ifade etmek bile imkansızdı.
Bununla birlikte Graham yukarı ok notasyonu adını verdiği bu yöntemle bu sayıyı yazmayı başardı. Bildiğiniz gibi çarpma aslında toplamanın kısa yoludur. Yani 3 x 3 = 3+3+3 anlamına gelmektedir. Benzer biçimde üslü sayılarda çarpmanın kısa yoludur. Yani 33 = 3 x 3 x 3 demektir. Tek ok işlemini, ↑ üs alma olarak tanımlayalım. Bu durumda 3↑3 = 33 = 3 x 3 x 3 = 27 biçiminde olacaktır.
Şimdi çift ok işlemini tanımlayalım. Yani 3↑↑3 = 3↑3↑3 = 333 = 327 = 7625597484987 olsun. Benzer biçimde devam edersek 3↑↑↑3 = 3↑↑3↑↑3 = 3↑↑(3↑↑3)=3↑↑(7625597484987) biçiminde bir sonuç elde ederiz.
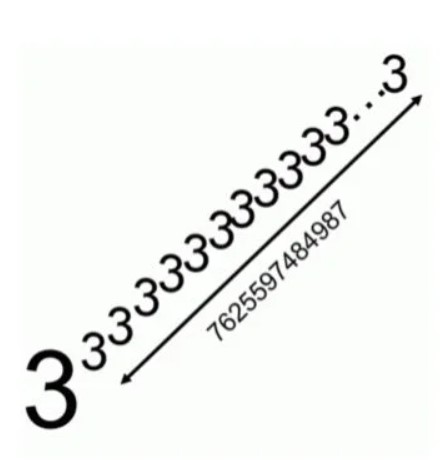
Gördüğünüz gibi bu devasa sayı 3 sayısının bir katı ve tamsayı. Ayrıca matematikçiler bu sayı hakkında ilginç bir bilgi daha öğrendiler. Sayı ne kadar büyürse büyüsün sonda gördüğünüz basamak aynı kalıyor. Yani bu sayının son her zaman 7 ile bitiyor.
En büyük sayıyı bulduk diye sevinmeyin. Graham sayısından daha büyük başka sayılar da vardır. Bunlardan birisi de Rayo sayısıdır. Bu sayı MIT Profesörü Agustin Rayo ve Princeton Profesörü Adam Elga arasında 26 Ocak 2007’de gerçekleşen “en büyük sayıyı kim bulabilir” yarışması sonucunda bulunmuştur.

Rayo Sayısı Graham’ı Geçer
Düelloda her turda bir yarışmacı tahtaya çıkıp, yeni bir sayı yazacaktı. Diğer yarışmacı da tamamen farklı bir yaklaşımla yani diğerinin yazdığı sayı artı bir demeden daha büyük bir sayı yazacaktı. Elga tahtanın başına geçer ve ilk hamle olarak “1” sayısını yazar.
Daha sonra Rayo tahtaya gelir ve bu 1 rakamının ardına yaklaşık 30 tane daha 1 yazar. Sonrasında Elga sadece baştaki iki tane 1 rakamını bırakacak şekilde diğer 1’lerin alt kısımlarını siler. Yani 11!!!!…! sayısını yazmıştır. Burada yaklaşık 30 tane faktöriyel vardır.
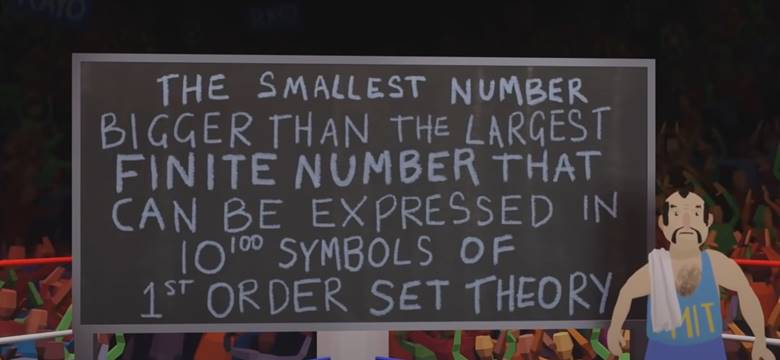
Daha sonra Rayo tahtaya çıkar ve BB(googol) sayısını yazar. Bu sayı “busy beaver” adı verilen bir fonksiyonla ilgilidir. En son olarak Rayo tahtaya çıkar ve de kendi kazanan sayısını tahtaya yazar. Aslında tahtaya yazdığı şey sayının kendisi değil, onun tanımıdır.
Tanım şuna benzer. “Birinci dereceden kümeler teorisinin googol tane sembolünü kullanarak ifade edilebilen en büyük sonlu sayıdan büyük en küçük sayı”. Elga kurallara uyacak bir şekilde başka sayı bulamaz. Bu durumda Rayo (10100) olarak gösterilen sayı yarışmayı kazanır. Günümüzde Rayo sayısının tahtını kimse elinden alamamıştır. Ancak bu sayının matematikte bir karşılığı da yoktur.
Ancak Graham sayısından çok çok daha büyük ve matematikte belli teoremlerin sonucunda karşımıza çıkan başka sayılar da vardır. TREE(3) veya daha da büyük bir sayı olan SSCG(3) gibi sayılar neredeyse tesadüfen bulunmuştur ve kendileri bir sonraki yazımızın konuları olacaktır.
Kaynaklar ve ileri okumalar
- These Numbers Are So Big They Literally Don’t Fit Inside The Universe. Yayınlanma tarihi: 11 Kasım 2022. Kaynak siste: Iff Science. Bağlantı: These Numbers Are So Big They Literally Don’t Fit Inside The Universe
- The Daddy of Big Numbers (Rayo’s Number) – Numberphile; yayınlanma tarihi: 12 Nisan 2020; bağlantı: https://www.youtube.com/
- Too big to write but not too big for Graham. Yayınlanma tarihi: 4 Temmuz 2017; Bağlantı: https://plus.maths.org/
- Ginormous Numbers Could Create a Mental Black Hole. Yayınlanma tarihi: 5 Şubat 2013. Kaynak site: Live Science. Bağlantı: Ginormous Numbers Could Create a Mental Black Hole
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel