Birçok insanın okuldaki matematik derslerine dair anıları hiç de güzel değildir. Buna bir neden olarak bu kişiler matematiksel düşünemediklerini iddia edecektir. Ancak gerçek şu ki matematiksel düşünce bir değil bir çok farklı biçimde gerçekleşir.

Bu nedenle eğer matematiği anlamakta zorlanıyorsanız belki de yapmanız gereken sadece bakış açınızı değiştirmektir. Buna bir örnek olarak gelin bu yazıda çoğumuzun geometri dersinde adını duyduğumuz bir elipsin tanımını farklı bakış açıları ile ele alalım. Bu esnada Dandelin küreleri ile de tanışalım. Göreceğiniz gibi basit bir matematiksel nesneyi bile düşünmenin birçok yolu vardır.
Elips Tanımı Nedir?
Günlük yaşantımızda çemberlerden sık sık söz ederiz. Ancak hayatımızın her günü çemberlerden çok daha fazla elips görürüz. Bir bardağa tepeden baktığımız zaman bardağın ağzını bir çember biçiminde görürüz. Ancak yandan baktığımızda göreceğimiz şekil hemen hemen bir elipstir.
Bazen oval olarak da adlandırdığımız elips simetrik kapalı bir şekildir. Çemberi hatırlayın. Çemberde bir merkez vardır. Çemberin çevresi ile bu merkez arasındaki uzaklık da her zaman eşittir. Oysa ki bir elipsin odak isimli iki merkezi vardır. Bu odaklar, elips için birleşik bir merkez görevi görür. Aslında bir çember özel bir elipstir. Çünkü iki odak noktası tek bir yerde kesişmektedir.
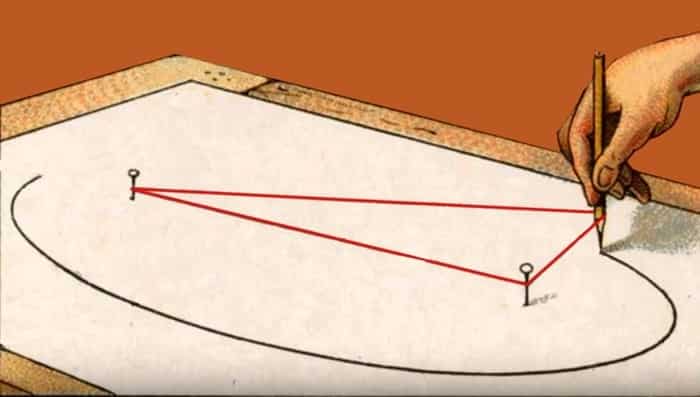
Elips çizmenin en bilinen yöntemi, bir düzleme iki çivi çakmak ve bu çivilere bir ip bağlamaktır. Kalemi ipe geçirip bir tur çevirdiğimizde ortaya elips çıkar. Öte yandan elipsin tanımı geometri yardımıyla da yapılır. Aslında elips konikler adı verilen bir eğri ailesine aittir.
Bunlar içi boş bir koninin çeşitli açılarda dilimlenmesiyle elde edilen eğrilerdir. Böyle bir koniyi aslında farklı biçimlerde keserek farklı eğriler elde ederiz. Bu eğriler aşağıda da göreceğiniz çember, parabol ve bir hiperbol olacaktır.
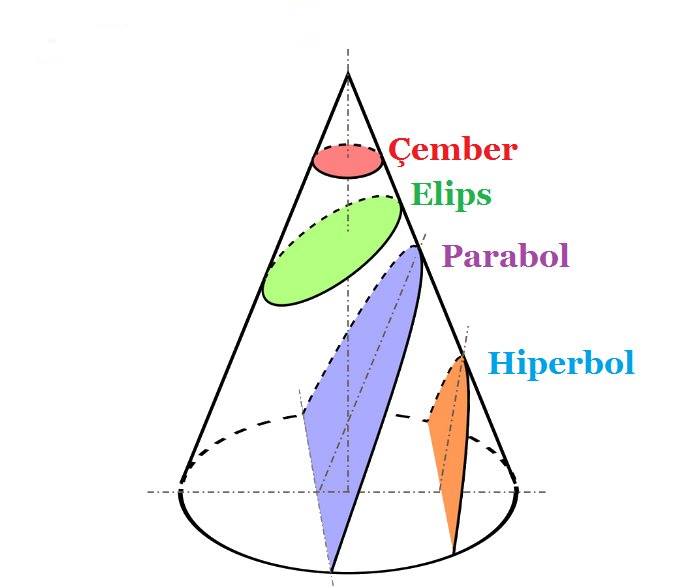
Elips hakkında bu biçimde yani görsel düşünme biçimiyle, onu birbiri ile ilişkili eğrilerden oluşan bir ailenin parçası olarak düşündünüz. Ancak herkes görsel düşünmeyi tercih etmez. Kimi insanlar söz konusu olan şey geometri bile olsa, matematiksel kavramları kelimelerle düşünmeyi tercih edecektir. Bu durum da elips tanımını aşağıdaki gibi de verebiliriz.
Elips Tanımını Cebirsel Düşünelim
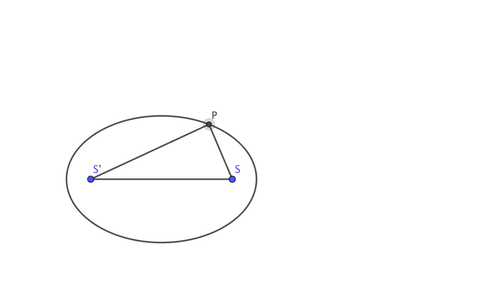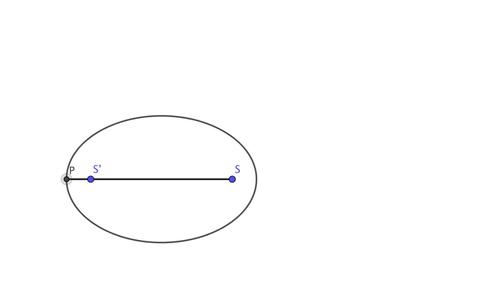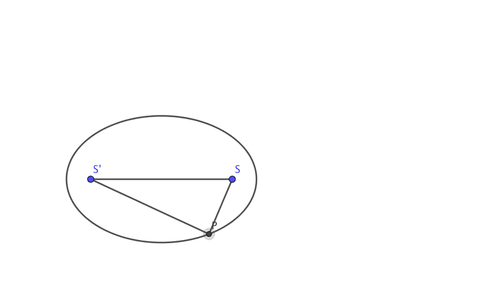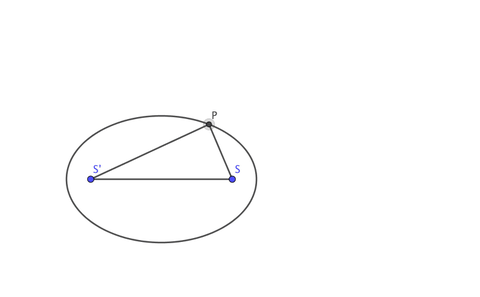
Bir elipsin tanımlayıcı bir özelliği, üzerindeki her nokta için, noktadan iki odak noktasına (çizimdeki iki çubuk) olan mesafelerin toplamının sabit olmasıdır. Yani bir elips, iki odak noktasını çevreleyen bir düzlemdeki eğridir, böylece iki odak noktasına olan mesafelerin toplamı eğri üzerindeki her nokta için sabittir.
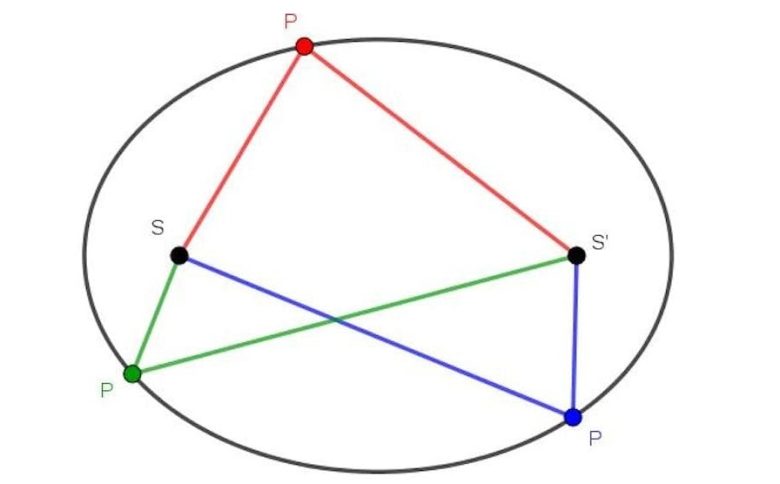
Ancak bu açıklama bazı kişiler için yeterli olmayacaktır. Sembollerle düşünmeyi seven biri için de PS+PS’=C (burada C bir sabittir) diyerek de bir elipsi tanımlayabiliriz. Cebirsel düşünmeye devam ederseniz bu sefer sizi yeni bir tanım bekleyecektir.
Konik kesitlerin her biri ikinci dereceden bir denklemle ifade edilebilir. Merkezi sıfır ve yarıçapı 1 olan ve bir koordinat sistemi üzerine çizilen daire, x 2 + y 2 = 1 denklemine sahiptir. Ancak elips denklemi biraz farklıdır çünkü merkezden eğriye olan mesafe sabit değildir.
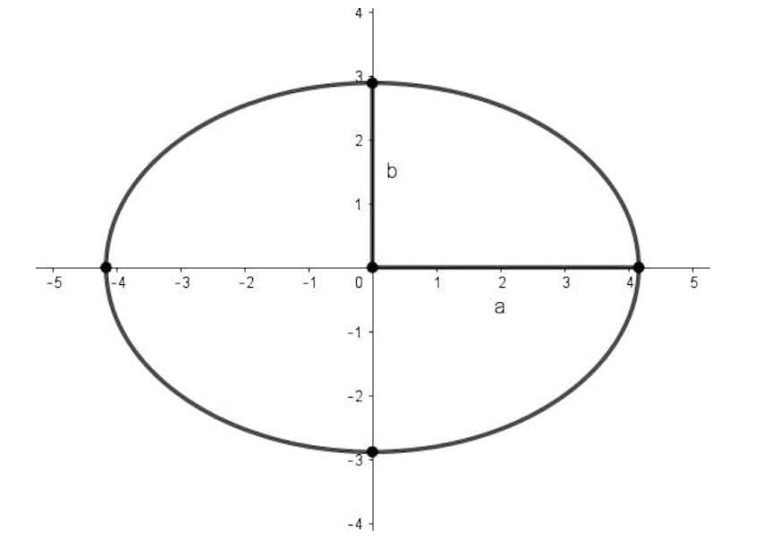
Burada a ve b uzunlukları elipsin ne kadar büyük (eliptik) olduğunu tanımlar ve bize elipsin denklemini verir. Denklem (x/a)2 + (y/b)2 = 1 biçimindedir. Bu noktaya kadar bir elipsi farklı biçimlerde tanımladık. Peki tüm bu elips tanımları arasında bir şey dikkatinizi çekti mi? Sizin çekmediyse bile on dokuzuncu yüzyılda Germinal Pierre Dandelin’in (1794–1847) çekmişti. Kendisi iki farklı elips tanımını (a) bir koninin enine kesiti veya (b) PA + PB’nin sabit olduğu bir eğri ilişkilendirmenin bir yolunu keşfetti.
Dandelin Küreleri Nedir?
Şimdi gelelim eşdeğerliliğin nasıl bulunduğuna. D düzlemi ile K konisinin ara kesiti, odakları F1 ve F2 olan elips olsun. Koniye ve elipse teğet olan iki tane küre vardır. Dandelin küreleri diye tanımlanan bu küreler M1 ve M2 merkezli kürelerdir. Şimdi, elips üzerinde herhangi bir P noktası alalım.
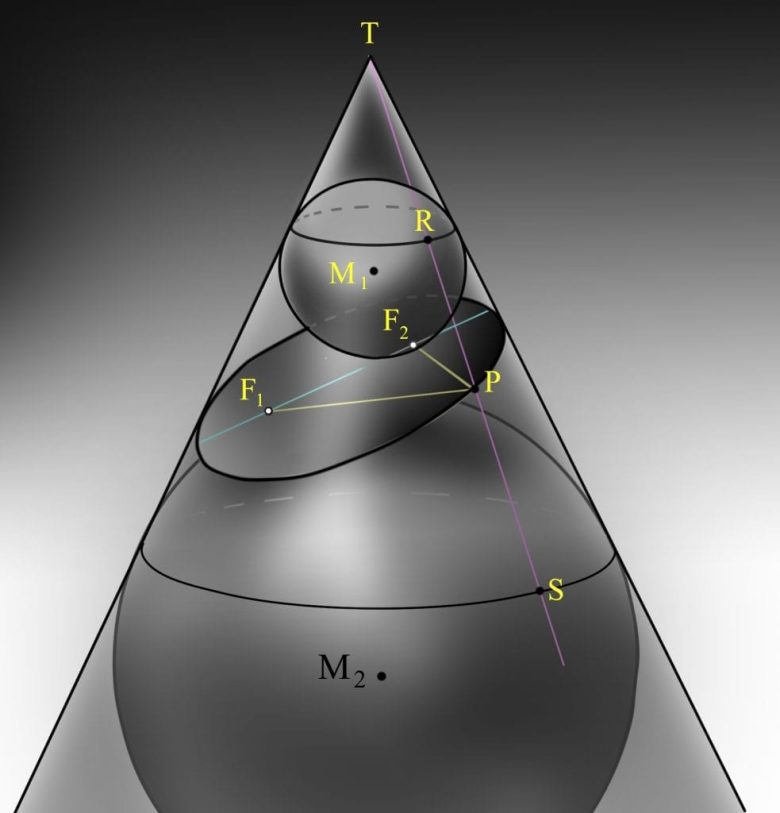
Burada elips üzerinde alınan her P noktası için, |PF1|+|PF2| toplamı sabittir, çünkü: |PF1| + |PF2| = |PR|+|PS| = |RS| olur. ( Detaylı ispata buradan erişebilirsiniz)
Sonuç olarak
Matematiksel kavramlar hakkında düşünmenin gördüğünüz gibi bir çok yolu vardır. Bu nedenle matematik ile uğraşırken sabit değil esnek bir bakış açısına sahip olmak önemlidir. Başarılı matematikçiler, herhangi bir problem için bazı stratejiler diğerlerinden daha iyi çalıştığından, yaklaşımlar arasında akıcı bir şekilde geçiş yapabilenlerdir.
Kaynaklar ve ileri okumalar
From visual to verbal – there’s more than one way to understand maths. Yayınlanma tarihi: Kaynak site: Conversation. Bağlantı: From visual to verbal – there’s more than one way to understand maths
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel