Dünyanın çevresine bir ip dolasak ne olurdu? İlk bakışta çocukça ya da anlamsız gibi görünen bu soru, aslında sezgilerimize meydan okuyan ve matematiğin gücünü ortaya koyan bir düşünce deneyine dönüşüyor.

Birazdan okuyacağınız ilk bulmaca 1702 yılına ait. İngiliz matematikçi ve doğa filozofu William Whiston (1667–1752) tarafından kaleme alınan bir ders kitabında yer alıyor. Bu bulmaca, matematik tarihinde bir dönüm noktası olarak görülmese de, sezgilerimizin ne kadar yanıltıcı olabileceğini göstermesi bakımından uzun süredir ilgi çekmeye devam ediyor.
İkinci bulmaca olan “dünyayı çevreleyen ip” sorusunun ise ilk olarak Henry Ernest Dudeney tarafından yazıya döküldüğü düşünülüyor.
Her iki bulmacada da düşünmeyi kolaylaştırmak için dünyanın mükemmel bir küre olduğunu ve yüzeyinin tamamen düzgün kabul edildiğini varsayacağız. İlk bakışta birbirinden farklı görünseler de, her iki soru aynı temel matematiksel ilkeye dayanıyor. Hazırsanız başlayalım.
1- Dünyanın Çevresinde Yürüyen Adam
Dünyanın çevresinde yürüyen bir adam hayal edin. Böyle bir durumda, adamın kafasıyla ayaklarının kat ettiği mesafelerin birbirine eşit olmaması gerekir. Peki ama bu fark ne kadar olabilir?
Sorunun biraz garip olduğunu kabul etmek gerek. Ancak bu bir düşünce deneyi; dolayısıyla “öyle olmaz” demeden, işe matematiksel bir yaklaşımla bakalım. Öncelikle bazı temel bilgileri hatırlayalım: bir çemberin çevresi, 2πr formülüyle hesaplanır. Yukarıdaki hayali diyagramda, r Dünya’nın yarıçapını ve H insanın boyunu temsil etsin. Bu durumda adamın ayaklarının izlediği yol, yani Dünya yüzeyine yakın çevre, 2πr olacaktır. Kafasının izlediği yol ise, yerden H kadar yüksekteki dairenin çevresi olduğu için 2π(r + H) biçiminde ifade edilir.
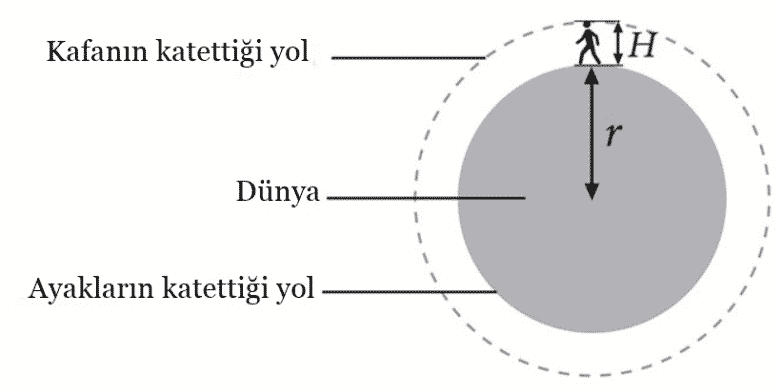
Bu iki çevre arasındaki farkı hesaplarsak: 2π(r + H) – 2πr = 2πr + 2πH – 2πr = 2πH.
Görüldüğü gibi 2πr terimleri birbirini götürür ve sonuç yalnızca 2πH olur. Yani fark, sadece insanın boyu ile orantılıdır. Örneğin eğer adamın boyu 1,8 metre ise, bu fark yaklaşık olarak 2 × 3,14 × 1,8 ≈ 11,3 metredir.
Bu sonuç şaşırtıcıdır: Dünya’nın çevresi yaklaşık 40.000 kilometre olmasına rağmen, bir kişinin kafası yürüyüş boyunca ayaklarından yalnızca 11 metre daha fazla yol alır. Sezgisel olarak çok daha büyük bir fark beklenebilir; fakat matematik bu konuda oldukça nettir. Şimdi ikinci bulmacaya geçelim. Aslında bu ikinci soru da benzer bir düşünce ve çözüm yaklaşımına sahiptir.
2- Dünyanın Çevresini Saran İp
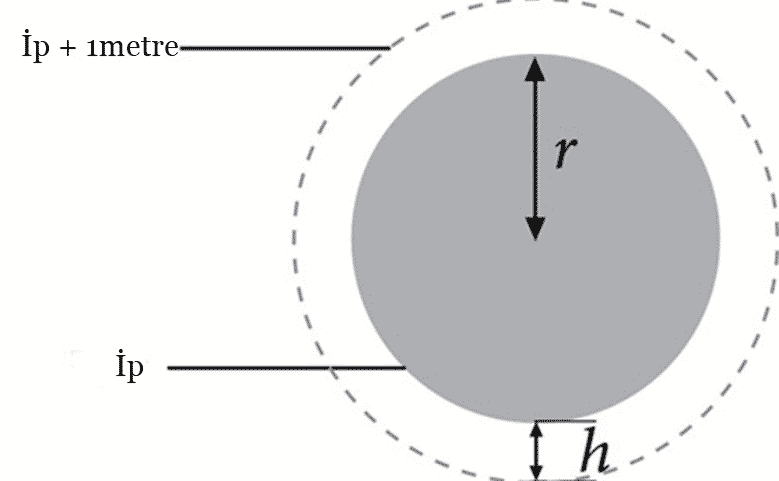
Elimizde çok uzun bir ip olduğunu ve bu ipi sıkı bir şekilde Dünya’nın çevresine sardığımızı hayal edelim. Daha sonra bu ipe sadece 1 metre ekleyelim ve tekrar Dünya’nın çevresine sarmaya çalışalım. Şimdi ipi, dünyanın yüzeyine her noktada eşit uzaklıkta olacak şekilde yukarı kaldıralım. Bu ipin altından hangi büyüklükte bir hayvan geçer?
Varsayalım ki Dünya’nın çevresi c uzunluğunda olsun. Uzatılmış ipin uzunluğu ise c + 1 olur. Çemberin çevresi formülünü kullanarak iki denklem kurabiliriz: 2πr = c ve 2π(r + h) = c + 1
- İkinci denklemde parantezi açarsak: 2πr + 2πh = c + 1
- Birinci denklemden 2πr = c olduğu için yerine yazdığımızda: c + 2πh = c + 1
- Buradan c’ler birbirini götürür ve geriye 2πh = 1 kalır. Bu denklemi h için çözersek: h = 1 / 2π
- Bu da yaklaşık 0,159 metre yani 15,9 santimetre eder.
Şimdi durup bir düşünelim: 40.000 kilometrelik bir ipi sadece 1 metre uzatıyoruz. Bu küçük fark, ipin dünyanın her yerinde yerden yaklaşık 16 santimetre yukarıda durmasına neden oluyor. Bu kadar küçük bir eklemenin bu kadar geniş bir etkiye sahip olması sezgisel olarak şaşırtıcıdır. Ve sorunun yanıtı da ilgi çekicidir. Bu boşluktan muhtemelen bir kedi ya da küçük bir köpek rahatça geçebilir.
İşin en ilginç yanıysa, bu sonucu elde etmek için Dünya’nın büyüklüğü hakkında hiçbir bilgiye ihtiyaç duymamış olmamızdır. Hesaplamalarda yalnızca eklenen ipin uzunluğu ve çemberin çevre formülü yer alıyor. Bu da bize, bazı problemlerde önemli olanın mutlak büyüklükler değil, aralarındaki ilişkiler olduğunu gösteriyor.
Sonuç Olarak
Her iki problemin de dikkat çekici yönü, yanıtlarının kürenin boyutundan tamamen bağımsız olmasıdır. Soruları ister Dünya için, ister Ay, hatta bir portakal için soralım, alacağımız cevap değişmez. Sonuç yalnızca ipin ne kadar uzatıldığına bağlıdır. Bu durum, sezgilerimize ters gelse de matematiksel açıdan son derece nettir.
Kaynaklar ve ileri okumalar:
- Alex Bellos; Can You Solve My Problems? A Casebook of Ingenious, Perplexing and Totally Satisfying Puzzles
- Wrapping a Rope around the Earth Puzzle (TANTON Mathematics). Kaynak: Youtube. Bağlantı: Wrapping a Rope around the Earth Puzzle (TANTON Mathematics)
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel