Sokaktaki herhangi birine “kaç boyut var?” diye sorduğunuzda, alacağınız cevap büyük ihtimalle “üç” olacaktır. Oysa ki, evrenin en az dört boyutlu olduğunu artık biliyoruz. Ancak bu bilgiye sahip olmamıza rağmen, çoğumuz dördüncü hatta beşinci boyutun ne anlama geldiğini hâlâ açıkça tarif edemiyoruz.

Dördüncü Boyut Nedir?
İçinde yaşadığımız dünya, katı biçimde 3 boyutludur: yukarı/aşağı, sağ/sol, ileri/geri. Hareket edebileceğimiz yönler yalnızca bunlardır. Ancak yıllardır hem bilim insanları hem de bilim kurgu yazarları, daha yüksek boyutlu uzayların olasılıklarını düşünüyor.
Peki, 4 ya da 5 boyutlu bir evren nasıl görünürdü? Ya da bazılarının öne sürdüğü gibi, biz zaten böyle bir çok boyutlu uzayda yaşıyor olabilir miyiz? Belki de bizim üç boyutlu dünyamız, daha yüksek boyutlu bir evrenin içinden geçen bir kesitten ibarettir. Tıpkı üç boyutlu bir küpten yapılan kesitte iki boyutlu bir kare elde edilmesi gibi…
Daha yüksek boyutlar gerçekten var mı? Bu soruya matematik şaşırtıcı derecede net bir yanıt veriyor. Nasıl ki iki boyutlu bir düzlem, bir koordinat sistemiyle (örneğin (5,6) gibi ikililerle) tanımlanabiliyorsa, üç boyutlu uzay da (5,6,3) gibi üçlü sayı kümeleriyle ifade edilebilir. Bu düşünceyi bir adım daha ileri taşıdığımızda, matematik açısından dört boyutlu uzay, (5,6,3,2) gibi gerçek sayıların oluşturduğu dörtlü kümelerle tanımlanır. Bu mantık, daha yüksek boyutlar için de aynı şekilde genişletilebilir.
Elbette bu, fizikçilerin sorduğu şu soruya doğrudan yanıt vermez. Bu boyutların nesnel fiziksel bir varlığı var mı? Ancak matematiksel olarak, eğer sayılara inanıyorsanız, dört boyutlu uzaya da inanmaktan başka çareniz kalmaz.

Fizikçiler, en azından kuramsal olarak, normal üç boyutumuzun ötesinde daha yüksek boyutların olabileceğini uzun süredir biliyor. Bu fikre dair ilk ipucu, 1905 yılında Einstein’ın özel görelilik kuramını geliştirmesiyle ortaya çıktı.
Ancak fizikçilerin burada söz ettiği, paralel evren gibi bilim kurgu dizilerinde sıkça yanlış anlaşılan bir kavram değildir. Aslında üç boyutun ötesinde, ek bir uzaysal boyut fikridir. Bu, bildiğimiz mekân algısının ötesinde yeni bir yön anlamına gelir.
Dördüncü Boyutu Neden Anlayamıyoruz?
Peki bu tamam da, bu uzaylar nasıl hayal edilebilir? İşte bu soru zordur, çünkü insan beyni üçten fazla boyutta görmeye programlı değildir.

1884 yılında İngiliz matematikçi Edwin A. Abbott, ek boyutlar kavramını açıklamak için Flatland adlı bir roman yazdı. Kurgu, iki boyutlu varlıklardan oluşan ve yalnızca uzunluk ile genişliğin var olduğu hayali bir evrende geçiyordu. Bu evrene Abbott, “Düzülke” adını vermişti.
Roman boyunca, tüm yaşamlarını bir masa yüzeyi gibi iki boyutlu bir düzlemde sürdüren Düzülkelilerin, üçüncü boyut fikrine neden bu kadar yabancı kaldıklarını görürüz. Abbott, bu örnekle aslında şunu söyler. Bizim de dördüncü boyuta karşı duyduğumuz şaşkınlık hâli, Düzülkelilerin üçüncü boyuta verdiği tepkinin aynısıdır.
Yine de, matematik burada yardımımıza koşar. Çünkü aşina olduğumuz uzaylardaki olayları daha yüksek boyutlara genelleştirme olanağı sunar. Bu konuda en açıklayıcı örneklerden biri küredir.
Bir nokta seçip, bu noktaya tam olarak 1 cm uzaklıktaki tüm noktaları işaretlediğinizde, ortaya 1 cm yarıçaplı bir çember çıkar. Aynı şeyi üç boyutlu uzayda yaparsanız, bu kez bir küre elde edersiniz. Ve işte heyecan verici kısım burasıdır. Bu işlemi dört boyutta da yapabilirsiniz—ve sonuçta ortaya çıkan yapı, ilk hiperküre olur.
Hiperküre, bizim hayal gücümüzün ötesindedir ama matematiksel olarak tamamen tanımlanabilir. Bu da yüksek boyutların görsel olarak sezilemese bile mantıksal olarak inşa edilebileceğini gösterir. Peki bu nasıl bir şeye benziyor?
Dördüncü Boyutu Nasıl Düşünebiliriz?
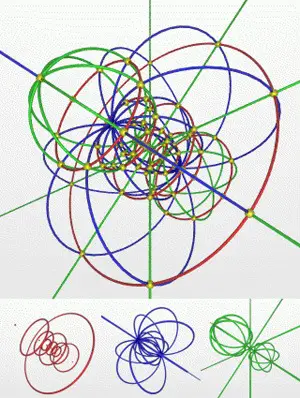
ve hipermeridyenlerini (yeşil) temsil eden yansıtmalardır.
Görsel: Claudio Rocchini,
Bir çemberi yakından incelediğinizde, her parçası size düz bir çizgi gibi görünür. Yani çember, aslında 1-boyutlu bir küre (1-küre) olarak da adlandırılır. Benzer şekilde, bildiğimiz küre (2-küre), yerel olarak düz bir iki boyutlu yüzey gibi görünür. Ancak tümüne bakıldığında, kenarı olmayan, yalnızca sonlu bir yüzey alanına sahip bir şekildir.
Aynı prensip, ilk hiperküre (3-küre) için de geçerlidir. 3-kürenin her bölgesi, tıpkı alıştığımız üç boyutlu uzay gibi görünür. Öyle ki, belki de biz şu anda zaten bir 3-kürenin içinde yaşıyoruz, ama farkında değiliz. Çünkü yerel düzeyde, her şey tanıdık görünür. Fakat 3-küre, düz uzayın aksine, kendi üzerine kıvrılır; kenarı yoktur, ama yalnızca sonlu bir hacme sahiptir.

Ve elbette burada durmuyoruz: Bir sonraki adım, 4-küredir. Bu yapının her parçası, dört boyutlu uzay gibi görünür. Aynı mantıkla bu süreç her boyutta devam eder. Her yeni hiperküre, kendi düzleminde “düz” gibi görünen ama genel yapısı itibariyle kıvrımlı ve sonlu olan bir geometrik varlıktır.
Fazladan Boyutların Topoloji İle İlgisi Nedir?
Geometri gibi, topoloji de şekillerin özelliklerini inceleyen bir matematik dalıdır. Bu alanın temel sorularından biri şudur. İki şekil ne zaman gerçekten aynı kabul edilir? En basit düzeyde, iki şekil birebir aynıysa ama farklı yerlerde duruyorsa, çoğu durumda bunları aynı sayarız. Ancak topolojide “aynılık” kavramı çok daha geniştir.
Topolojik bakışa göre, bir şekil, kesmeden ya da yapıştırmadan çekilip uzatılarak başka bir şekle dönüşebiliyorsa, bu iki şekil aynıdır. Bu yüzden, bir topolog için üçgen, yedigen, yamuk gibi çokgenlerin hepsi aynı şeydir: sadece bir çember. Çünkü hepsi düzgünce bükülerek çembere dönüşür.

Öte yandan, bir “sekiz” figürü gerçekten farklıdır. Çünkü onu bir çembere çevirmek için kesmek gerekir ve bu, topolojide yasaktır. Bu tür delikler çekerek veya bükerek yok edilemezler.
Peki hiç deliği olmayan şekiller hangileridir? Poincaré varsayımı bu soruya zarif bir yanıt verir: Deliği olmayan tek şekil küredir. Bu, geometrik bakış açısından doğru değildir çünkü küpler, piramitler gibi birçok şeklin de deliği yoktur. Ancak bir topoloğa göre, bunların hepsi aslında “küre”dir.
2002 yılında bu varsayımın doğru olduğu kanıtlandı. Poincaré’nin orijinal sorusu 3-boyutlu küreyle ilgiliydi, ancak aynı durum daha yüksek boyutlar için de geçerli.
1956’da matematikçi John Milnor, 7 boyutlu şekiller üzerinde çalışırken garip bir yapıyla karşılaştı. Bu şekil, deliği olmayan bir küre gibi görünüyordu ama eğriliği sıradan bir küreden çok farklıydı. İlk başta bunun Poincaré varsayımına karşı bir örnek olduğunu düşündü. Ancak daha dikkatli incelediğinde, bu şeklin gerçekten de bir küreye dönüştürülebileceğini gördü. Milnor bu şekilde ilk egzotik küreyi keşfetmişti.
1, 2 ve 3 boyutlu uzaylarda egzotik küre yoktur. 5. ve 6. boyutlarda da sadece sıradan küreler vardır. Ama 7. boyutta birdenbire tam 28 tane egzotik küre ortaya çıkar. Ancak dördüncü boyutta hiçbir egzotik küre bulunamadı. Aynı zamanda, böyle bir yapının var olmadığını kanıtlayabilen kimse de çıkmadı.
Dördüncü Boyutun Tuhaf Dünyası

Çoğu matematikçi 4-boyutlu egzotik kürelerin var olduğuna inanıyorlar. Bunun nedeni, 4-boyutlu uzayın halihazırda çok tuhaf bir yer olması; içinde akıl almaz şeylerin mümkün olması. Dört boyutta sadece kürelerin egzotik versiyonları yok. 4-boyutlu uzayın kendisi bile (R⁴, yani 4-boyutlu Öklid uzayı) farklı türlerde var olabiliyor. Normalde düz ve bildiğimiz uzay olan R⁴ dışında, ona topolojik olarak eş ama diferansiyel olarak farklı olan egzotik R⁴ versiyonları da mevcut. 1987’de Clifford Taubes, bu türden sonsuz sayıda egzotik R⁴ olduğunu gösterdi.
Bu açıdan bakıldığında, 4. boyut diğer tüm boyutlardan çok daha garip ve karmaşık bir yer. Çünkü diğer tüm boyutlar için (örneğin R³, R⁵ gibi) yalnızca tek bir versiyon bulunur. Ancak R⁴’ün sonsuz sayıda versiyonu vardır. Belki de bu yüzden, bilim kurgu yazarlarının hayal ettiği garip evrenlerin matematiksel karşılığı gerçekten de 4. boyutta yatıyor olabilir.
Kaynaklar ve ileri İleri Okumalar:
- How many dimensions are there? Yayınlanma tarihi: 28 ocak 2021; Kaynak site: ZME Scince. Bağlantı: How many dimensions are there?
- Exotic spheres, or why 4-dimensional space is a crazy place. Kaynak site: Plus Math. Yayınlanma tarihi: 12 Ocak 2011. Bağlantı:
Exotic spheres, or why 4-dimensional space is a crazy place
Matematiksel





