İnsan beyni, basit ve düz çizgileri tercih eder. Bu nedenle, insanlar değişkenlerle sonuçlar arasındaki ilişkilerin genellikle doğrusal olmasını bekler. Çoğu zaman bu beklenti doğrudur. Ancak doğrusal olmayan olgular hayatımızda her yerdedir. Bu tür ilişkilerin farkına varmazsanız, yanlış kararlar verme olasılığınız artar. Ancak veriler arasındaki ilişkileri görselleştirirseniz, bu ilişkilerin doğrusal olup olmadığını ve nasıl işlediğini görebilirsiniz.

Doğrusal olmama, bağımsız değişken ile bağımlı değişken arasında düz, sabit oranlı ya da doğrudan bir ilişki bulunmadığını ifade eden istatistiksel bir terimdir. Bu tür ilişkiler genellikle karmaşıktır ve anlaması daha zordur. Bunu daha iyi kavrayabilmek için önce doğrusal bir ilişkiye bakalım.
Diyelim ki bir miktar ip satın almak istiyorsunuz. İpin metresi 2 TL. Bu durumda, 2 metre ip için 4 TL, 6 metre için 12 TL ödemeniz gerekir. Genel bir ifadeyle, x metre ip alırsanız 2x TL ödeme yaparsınız. Burada açıkça görülen bir ilişki var: Aldığınız metre arttıkça, ödediğiniz tutar da aynı oranda artıyor. Bu ilişkiyi bir denklemle göstermek istersek, p(x) = 2x yazabiliriz.
Bu bir doğrusal ilişkidir. Bu ilişkiyi tanımlayan fonksiyona doğrusal fonksiyon denir. Neden böyle adlandırıldığını görmek için bu fonksiyonu bir koordinat sistemine çizebilirsiniz. Grafiği çizdiğinizde, karşınıza düz bir doğru çıkar. Bu da ilişkiyi doğrudan ve sabit oranlı olarak tanımlar.
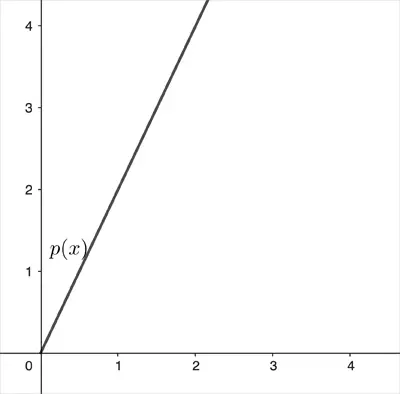
Doğrusal bir ilişkiyi tanımladıktan sonra, daha fazla ip almanızın bütçenizi aşıp aşmayacağını anlamak oldukça kolaydır. Diyelim ki elinizde belirli bir miktar ip var ama daha fazlasına ihtiyacınız var. Bu durumda, “a” metre daha ip alırsanız ne kadar ödemeniz gerektiğini merak ediyorsunuz.
Artık, bu tür sorulara yanıt vermek basittir. Çünkü bu noktada artık toplam fiyata değil, sadece artışa odaklanabilirsiniz. Önceki örneğimizde olduğu gibi, ipin metresi 2 TL ise, “a” metre daha ip almak size tam olarak 2a TL’ye mal olur.
Bu sonucu denklemsel olarak görmek isterseniz, toplam fiyat p(x+a) = 2(x+a) olur. Bu da açıldığında p(x+a) = 2x + 2a şeklindedir. Buradan da görüldüğü gibi, ödemeniz gereken ek tutar yalnızca 2a TL’dir. Önceki toplam tutarı bilmenize gerek kalmadan, sadece artan miktar üzerinden hesap yapabilirsiniz. Bu, doğrusal ilişkilerin sunduğu en büyük kolaylıklardan biridir.
Doğrusal Olmayan İlişki Nedir?
Almak istediğiniz kumaş kare şeklindeyse ve bir kenarının uzunluğu x metre ise, bu kumaşın alanı x² metrekare olur. Kumaşın metrekare başına maliyeti 2 TL ise, ödemeniz gereken toplam tutarı tanımlayan fonksiyon şu şekilde yazılır: P(x) = 2x²
Bu, doğrusal olmayan bir ilişkidir. Neden doğrusal olmadığını anlamak için bu fonksiyonu bir koordinat sistemine çizebilirsiniz. Grafiğin düz bir çizgi değil, yukarı doğru kıvrılan bir eğri olduğunu görürsünüz. Bu, artış oranının sabit olmadığı anlamına gelir. Kenar uzunluğu arttıkça, ödemeniz gereken miktar daha hızlı büyür.
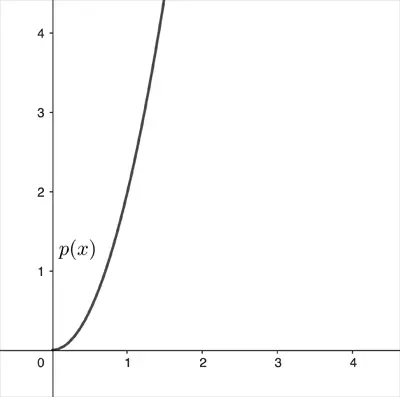
Şimdi karenizin kenar uzunluğunu a metre artırmak isterseniz ne olur? Elbette karenin alanı (x+a)2 metrekare olacaktır. Peki bu durumda ne kadar fazladan para ödemeniz gerekecektir? Cevap aşağıdaki gibidir.
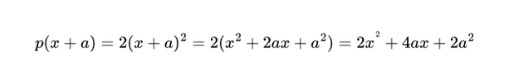
Bu durumda aradaki fark da p(x+a)-p(x)=4ax+2a2 biçiminde olacaktır. Bu sonuç, doğrusal olmayan ilişkinin temel özelliğini açıkça gösterir. Ek ödeme sadece a’ya değil, aynı zamanda mevcut kenar uzunluğu olan x’e de bağlıdır. Yani, kumaşın boyutunu büyütmek için harcayacağınız para, doğrusal bir şekilde değil, giderek artan bir şekilde yükselir.
Doğrusal Olmayan İlişkiler Nerede Karşımıza Çıkar?

İşte bu yüzden, doğrusal olmayan ilişkilere dayalı tahminler yapmak her zaman kolay değildir. Bu tür ilişkiler, değişkenler arasındaki etkileşimlerin sabit olmadığı ve sonuçların doğrudan öngörülemediği durumları içerir. Bazı durumlarda ise doğrusal olmayan denklemler, davranışlarının tahmin edilmesinin neredeyse imkânsız olduğu kaotik sistemlerin ortaya çıkmasına yol açabilir.
Bu duruma verilebilecek en bilinen örnek hava durumudur. Hava tahminlerinde kullanılan temel denklemler, doğrusal olmayan yapılara sahiptir ve bu yapılar genellikle kaotik davranış gösterir. Bu nedenle, bir ay ya da bir yıl sonrasına dair kesin hava tahminleri yapmak mümkün değildir. Küçük bir değişkenin bile büyük farklılıklar yaratabildiği bu sistemlerde, uzun vadeli tahminler güvenilirliğini hızla yitirir.
Bu noktada karşımıza kaos teorisi çıkar. Kaos teorisi, küçük değişikliklerin büyük sonuçlar doğurabileceği sistemleri inceleyen bir yaklaşımdır. Doğrusal olmayan sistemlerin karmaşıklığını anlamak için geliştirilen bu teori, modern bilimin birçok alanında, özellikle de doğa olaylarının modellenmesinde önemli bir yer tutar.
Kaynaklar ve ileri okumalar
- Maths in a minute: Non-linearity. Yayınlanma tarihi: Kaynak site: bağlantı: Maths in a minute: Non-linearity
- Smith, Karen. “What Is a Non Linear Relationship?” sciencing.com, https://sciencing.com/non-linear-relationship-10003107.html. 11 January 2024.
- Hayes AM, Laurenceau JP, Feldman G, Strauss JL, Cardaciotto L. Change is not always linear: the study of nonlinear and discontinuous patterns of change in psychotherapy. Clin Psychol Rev. 2007 Jul;27(6):715-23. doi: 10.1016/j.cpr.2007.01.008. Epub 2007 Jan 19. PMID: 17316941; PMCID: PMC3163164.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





