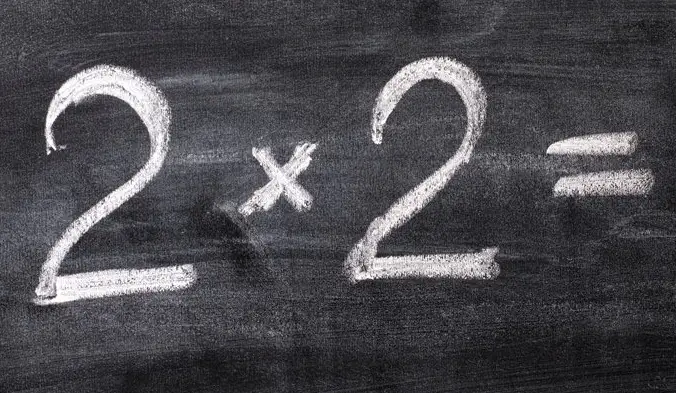Diferansiyel denklemler, matematiğin derinliklerinde yatan ve bilimden mühendisliğe, biyolojiden ekonomiye kadar birçok disiplini şekillendiren güçlü araçlardır.
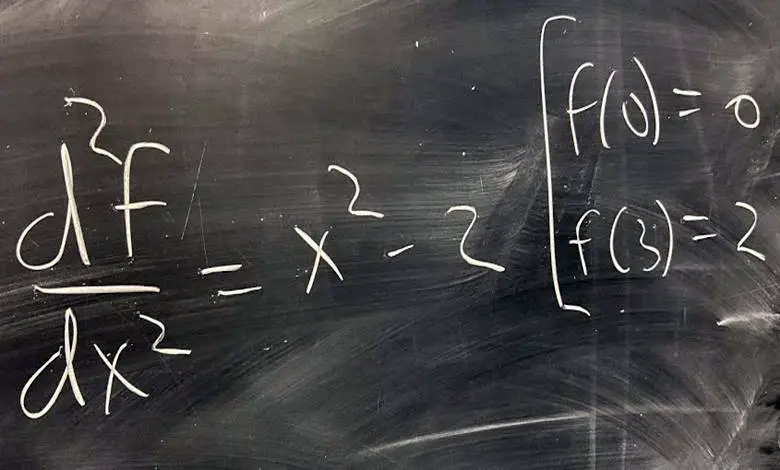
Bir ya da birden fazla fonksiyonun türevlerini ilişkilendiren bu denklemler, değişim ve hareketin temel dinamiklerini anlamamıza olanak sağlar. Fiziksel olaylardan toplumsal süreçlere kadar pek çok olguyu modellemek için diferansiyel denklemler kullanılmaktadır.
Bu yazıda, klasik ders notlarının ötesine geçerek diferansiyel denklemlerin nasıl çalıştığını anlamaya çalışacağız. Ürkütücü görünebilen matematiksel ifadelerin arkasında, aslında oldukça basit ve sezgisel bir mantığın yattığını keşfedeceksiniz.
Diferansiyel Denklemler Nedir ve Neden Önemlidir?
Otobanda saatte 70 kilometre sabit hızla araba sürdüğünüzü hayal edin. Bu hızla devam ettiğinizde, hedefinize 2 saat içinde ulaşacağınızı biliyorsunuz ve toplamda 140 kilometre yol kat edeceğinizi kolayca hesaplıyorsunuz. Bu basit örnek, diferansiyel denklemlerin temel konusunu anlamamıza yardımcı olur.

Diferansiyel denklemler, dünyadaki değişimleri ve bu değişimlerin oranlarını matematiksel olarak ifade eder. Temelde, bir sistemin mevcut durumunu ve bu durumun değişim hızını ilişkilendirerek gelecekteki durumunu tahmin ederler.
Çevremizdeki dünyayı anlamak için matematiği kullanmaya başladığınızda – ister bir bitkinin büyümesini, ister borsadaki dalgalanmaları, isterse bir hastalığın yayılmasını inceleyin – kısa sürede türevlerle ve diferansiyel denklemlerle çalıştığınızı fark edeceksiniz.
Adi Diferansiyel Denklem Nedir?
Diferansiyel denklem, temel olarak bir fonksiyon ile bu fonksiyonun türevlerini ilişkilendiren matematiksel bir ifade olarak tanımlanır. Araba örneğimize geri dönelim. Bu durumda, y mesafeyi, x ise zamanı temsil etsin. Alınan yolu tanımlamak için y(x) = 70x biçiminde bir fonksiyon kullanabiliriz. Eğer arabayı 2 saat boyunca sürdüyseniz, bu durumda x = 2 yerine koyularak y(2) = 70 × 2 = 140 km sonucuna ulaşırız.
Bu örnek, hızın mesafenin zamana göre değişim oranı olduğunu gösterir. Matematiksel olarak ifade edildiğinde, bu oran mesafenin zamana göre birinci türevini verir. Yani, dy/dx yazıldığında, bu hız anlamına gelir. Örneğimizde sabit bir hız olduğu için bu oran dy/dx = 70 biçiminde yazılmalıdır. Bu ifade, bir adi diferansiyel denklem (Ordinary Differential Equation) örneğidir.

Mesafenin zamana göre ikinci türevini aldığınızda, hızın zamana göre değişimini yani ivmeyi bulursunuz. İkinci türev, yalnızca hızın değişimini değil, aynı zamanda hareketin ne kadar hızlandığını veya yavaşladığını da analiz etmenize olanak tanır.
Adi diferansiyel denklemler, yalnızca bir bağımsız değişkene (örneğin, zaman) bağlı bir y niceliğini ve bunun türevlerini içerir. Daha yüksek dereceli türevlerle çalışmak, bir sistemin davranışını daha ayrıntılı bir şekilde modellemek için daha karmaşık denklemleri çözmek anlamına gelir.
Diferansiyel Denklemler Ne İşimize Yarar?
Diferansiyel denklemler, matematiğin ve bilimin modern dünyadaki birçok uygulamasının kalbinde yer alır. Bu denklemler, fizik, biyoloji, kimya, mühendislik ve finans gibi pek çok alanda hayati bir rol oynar. Aslında, günlük hayatımızda karşılaştığımız birçok problem ve matematiksel model bir şekilde diferansiyel denklemleri içerir.
Doğa yasalarının çoğu, diferansiyel denklemler biçiminde ifade edilmektedir. Maxwell’in elektromanyetizmayı açıklayan denklemleri ve Einstein’ın genel görelilik teorisi kapsamında yerçekimini tanımlayan denklemleri buna örnek olarak verilebilir. Bu denklemler, fonksiyonlar ve bu fonksiyonların türevleri arasındaki ilişkileri ifade ederek, doğadaki değişimi matematiksel bir çerçeveye oturtur.
Diferansiyel denklemler, matematikçilerin yüzyıllardır çözmeye çalıştığı karmaşık problemler sunar. Ne yazık ki, tüm diferansiyel denklemleri çözebilecek genel bir yöntem mevcut değildir. Bu nedenle, farklı türdeki diferansiyel denklemler için farklı çözüm yöntemleri geliştirilmiştir. Bu yöntemler, analitik çözümlerden sayısal tekniklere kadar geniş bir yelpazeye yayılır. Ancak tüm bu yöntemlerin ortak amacı, değişimi matematiksel olarak anlamak ve modellemektir.
Sonuç olarak
Diferansiyel denklemleri anlamanın en temel gerekliliği, kalkülüs konularına hakim olmaktır. Kalkülüs, türev ve integral kavramlarını içerir ve bu kavramlar diferansiyel denklemlerin temel taşlarıdır. Doğal dünyada her şey sürekli değişir, bu yüzden onu incelemek için değişimi anlamanın bir yoluna ihtiyacınız vardır. Ve bunu kalkülüs başarmıştır.
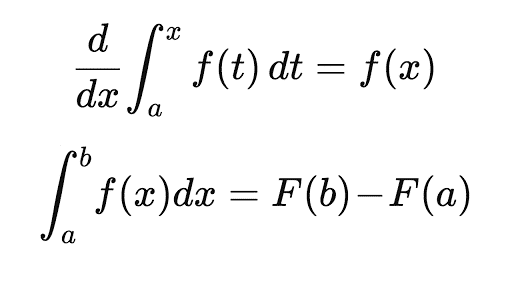
İntegraller ve diferansiyeller, genellikle insanları korkutacak şekilde sunulsa da çevremizdeki dünyayı anlama biçimimiz için bir zemin sağlar. Diferansiyel denklemleri öğrenmek zaman alır ve sabır gerektirir. Öğrendiklerinizi pekiştirmek için bol bol pratik yapmalısınız. Çeşitli kaynaklardan problemler çözmek ve gerçek dünya uygulamalarına odaklanmak, bu süreçte büyük fayda sağlar.
Kaynaklar ve ileri okumalar:
- Maths in a minute: Differential equations; Yayınlanma tarihi: 6 Mayıs 2020; Kaynak site: Plus math. Bağlantı: Maths in a minute: Differential equations/
- Why We Use Differential Equations and Their significance. Kaynak site: Medium. Yayınlanma tarihi: 29 Kasım 2023. Bağlantı: Why We Use Differential Equations and Their significance.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel