Yüzyılı aşkın bir süredir fizikçiler ve matematikçiler, sıvıların hareketini ve içlerindeki parçacıkların davranışını tek bir matematiksel çerçevede birleştirme arayışındaydı. Şimdi Michigan Üniversitesi’nden bir ekip, bu sorunu çözerek David Hilbert’in 1900’de ortaya koyduğu ünlü meydan okumalardan birini yerine yanıt verdi. Bu yanıt sonucunda Hilbert’in altıncı problemi çözülmüş olabilir.
Dünyanın en büyük matematikçisi geleceğe dair bir vizyon sunduğunda, matematik dünyası bunu dikkate alır. 1900 yılında Paris’teki Sorbonne Üniversitesi’nde düzenlenen Uluslararası Matematikçiler Kongresi’nde tam olarak bu yaşandı.
Dönemin dev ismi olan David Hilbert, 20. yüzyıla rehberlik edecek 10 çözülmemiş problemi açıkladı. Daha sonra bu listeyi 23 probleme çıkardı. Bu problemlerin matematiksel düşünce üzerindeki etkisi son 125 yılda derin oldu.

Hilbert’in altıncı problemi en iddialılarından biriydi. Hilbert’in altıncı problemi şunu istiyordu:
Fizikte kullanılan temel teorilerin, özellikle mekaniğin ve olasılığın aksiyomatik bir şekilde temellendirilmesi gerekiyordu. Yani, fiziksel yasalar da matematikteki gibi açık, kesin tanımlarla, tutarlı ve mantıklı bir sistem içinde formüle edilmeliydi.
Neyse ki Hilbert, bazı daha somut alt hedefler de belirlemişti. Araştırmacılar o zamandan beri bu hedeflere doğru adım adım ilerliyor.
Mart ayında, Chicago Üniversitesi’nden Yu Deng ile Michigan Üniversitesi’nden Zaher Hani ve Xiao Ma, bu alt hedeflerden birine önemli bir katkı sunduklarını iddia eden bir makale yayımladılar. Araştırmacılar, sıvıların hareketini açıklayan üç fizik teorisini birleştirmeyi başardıklarını öne sürüyorlar. Bu teoriler uçak tasarımından hava durumu tahminine kadar pek çok mühendislik uygulamasının temelini oluşturuyor.
David Hilbert’in Altıncı Problemi Nedir?
Her teori, sıvıların farklı ölçeklerdeki davranışını ele alır. Mikroskobik düzeyde sıvılar, küçük bilardo topları gibi çarpışan parçacıklardan oluşur. Bu ölçekte, Newton’un hareket yasaları parçacıkların hareketini başarıyla açıklar.
Ancak biraz daha geniş bir açıdan bakıp milyarlarca parçacığın toplu davranışını incelediğimizde, her birini ayrı ayrı modellemek pratik olmaktan çıkar. 1872 yılında Avusturyalı fizikçi Ludwig Boltzmann, bu soruna çözüm olarak Boltzmann denklemini geliştirdi. Bu denklem, her parçacığın izini sürmek yerine, tipik bir parçacığın olası davranışlarını istatistiksel olarak modellemeye dayanır.

Bu şekilde, küçük ölçekli ayrıntılar yerine daha büyük ölçekli eğilimler ön plana çıkar. Bu yaklaşım, fizikçilerin, her çarpışmayı tek tek hesaplamaya gerek kalmadan bir sıvının momentum ve ısı iletkenliği gibi özelliklerinin zamanla nasıl değiştiğini öngörmelerini mümkün kılar.
Daha da uzaklaştığımızda, makroskobik dünyaya ulaşırız. Bu ölçekte sıvılar, ayrı parçacıklardan oluşan bir sistem gibi değil, kesintisiz bir madde gibidir..
Mikroskobik, mezoskopik ve makroskobik olmak üzere bu üç analiz seviyesi, aslında aynı temel gerçeği, yani sıvıların akışını açıklamaya çalışır. İlkeler düzeyinde her teori, kendinden bir önceki teorinin doğal bir uzantısı olmalıdır.
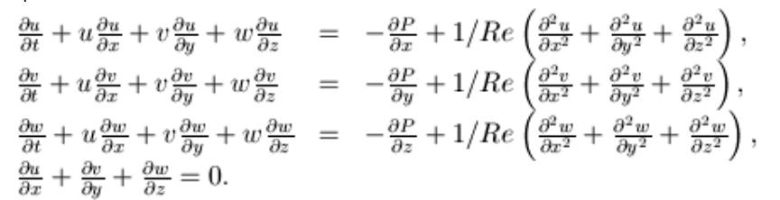
Makroskobik seviyedeki Euler ve Navier-Stokes denklemleri, mezoskopik seviyedeki Boltzmann denkleminden türemelidir. Boltzmann denklemi de mikroskobik seviyedeki Newton’un hareket yasalarından mantıksal olarak çıkarılmalıdır. İşte bu, David Hilbert’in 6. probleminde istediği türden bir “aksiyomatizasyon” örneğidir.
Fizik Yasalarını Birleştirmek
Akışkanlar dinamiğinde bu üç farklı bakış açısını birleştirmek, alanın uzun süredir çözülemeyen sorunlarından biriydi. Yeni ispat temel olarak üç adım üzerinden ilerliyor. İlk olarak, makroskobik teoriyi mezoskopik teoriden türetmek gerekiyor. Ardından, mezoskopik teoriyi mikroskobik düzeyden türetmek hedefleniyor. Son adımda ise tüm bu bağlantıları birleştirerek makroskobik yasaları doğrudan mikroskobik temellerden elde etmek amaçlanıyor.
İlk adım kolaydı. Hatta Hilbert’in kendisi bu alana önemli katkılar yapmıştı. Ancak mezoskopik teoriyi doğrudan mikroskobik temelden türetmek, çok daha zorlayıcı bir matematiksel problem olarak uzun süre çözüm bekledi.
Çünkü mezoskopik düzey, çok büyük sayıda parçacığın toplu davranışını konu alıyordu. Araştırmacılar bu noktada şu soruyu sordu. Eğer çarpışan parçacıkların sayısını sonsuza çıkarır ve her bir parçacığın boyutunu sıfıra indirirsek, Newton’un hareket denklemleri nasıl bir davranış biçimi gösterir?
Gösterdikleri şey şuydu: Bu uç sınırlarda, sistemin istatistiksel davranışı, yani sıvı içerisindeki tipik bir parçacığın olası hareketleri, Boltzmann denkleminin çözümüne yaklaşarak dengeli bir yapıya ulaşıyor. Böylece mikroskobik düzey ile mezoskopik düzey arasında sağlam bir matematiksel köprü kurmuş oldular.
Bu adımda karşılaşılan en büyük zorluk, incelenen zaman diliminin uzunluğu oldu. Daha önce, yalnızca çok kısa zaman aralıklarında Newton yasalarından Boltzmann denklemine geçişin mümkün olduğu biliniyordu. Oysa gerçek dünyada sıvılar uzun süre boyunca akışlarını sürdürür.
Uzun zaman dilimlerini ele almak, çok sayıda çarpışmayı ve geçmişteki etkileşimlerin güncel davranışlar üzerindeki etkisini hesaba katmayı gerektiriyordu. Deng, Hani ve Ma, her bir parçacığın geçmişinin şimdiki hareket üzerindeki etkisini ayrıntılı şekilde analiz ettiler. Geliştirdikleri yeni matematiksel tekniklerle, geçmiş çarpışmaların toplam etkisinin küçük kaldığını gösterdiler.
Uzun zaman ölçeği sorununu aşarak ve Boltzmann denkleminden Euler ve Navier-Stokes denklemlerinin türetilmesi üzerine yapılan önceki çalışmaları da birleştirerek, akışkanlar dinamiğinin üç büyük teorisini ortak bir çerçevede toplamayı başardılar.
Bu sonuç, farklı ölçeklerde farklı yaklaşımlar kullanmanın doğru ve geçerli olduğunu matematiksel olarak temellendiriyor. Çünkü en sonunda, tüm bu teoriler aynı fiziksel gerçeğe ve birleşik bir kuramsal yapıya bağlıdır.
Sonuç olarak
Eğer bu ispat doğruysa, David Hilbert’in altıncı Problemi için programında önemli bir dönüm noktası anlamına gelir. Belki de burada olduğu gibi, yeni yöntemlerle yaklaşarak Hilbert’in diğer zorlu problemlerinde de engeller aşılacaktır. Bu sayede fizik bilgisi önümüzde daha özgür ve kapsamlı bir şekilde akmaya devam eder.
Kaynaklar ve ileri okumalar
- Mathematicians solve 125-year-old problem to unite key laws of physics Yayınlanma tarihi: 14 Mart 2025. Kaynak site: New Scientist. Bağlantı: Mathematicians solve 125-year-old problem to unite key laws of physics
- Mathematicians Crack 125-Year-Old Problem, Unite Three Physics Theories. Yayınlanma tarihi: 14 Nisan 2025. Kaynak site: Scientific American. Bağlantı: Mathematicians Crack 125-Year-Old Problem, Unite Three Physics Theories
- Gao, Shan. (2025). Comment on “Hilbert’s Sixth Problem. Derivation of Fluid Equations via Boltzmann’s Kinetic Theory” by Deng, Hani, and Ma. 10.48550/arXiv.2504.06297.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel