Bernhard Riemann: Görelilik Teorisinin Temellerini Atan Dahi Matematikçi

Dünyanın en zor ve en ünlü matematik probleminin ne olduğunu belirlemek elbette tam olarak mümkün değil. Ancak, Bernhard Riemann tarafından 1859’da ortaya atıldığından beri matematikçileri şaşkına çeviren Riemann Hipotezi bunun için bir aday gibi gözüküyor. Bernhard Riemann adı, bir çok kişiyi şaşkına çeviren Riemann geometrisinde de yaşıyor.

Üstelik geliştirdiği Riemann geometrisinin Einstein’in genel görelelik teorisinin temellerini attığı da biliniyor. Zamanında kendisi hakkında pek konuşmayı sevmese de bu matematikçi kesinlikle hatırlanmayı hak ediyor.

Riemann, fiziğin yanı sıra matematiğin çeşitli dallarıyla ilgilenen olağanüstü derecede çok yönlü bir matematikçiydi. Bugün matematikte seksene yakın kavram da Riemann adı ile karşılaşabilirsiniz. Ayrıca, Ay’ın üzerindeki 110 km çapında bir kratere de onun adı verilmiştir. 4167 kod numaralı gezegen de onun adını taşır.

Bernhard Riemann Kimdir?

17 Eylül 1826’da Almanya’nın Breselenz kentinde doğan Bernhard Riemann bir din adamının altı çocuğundan biri olarak hayata başladı. On yaşına kadar babası onun eğitimiyle kendi ilgilendi. Yirmi yaşında ilahiyat okumak eğitimine başladı. Ancak ilerleyen süreçte babasının da desteği ile Göttingen Üniversitesi’ne kaydoldu.

Bir çok önemli matematikçinin yanı sıra öğretmenlerinden biri de Carl Frideric Gauss idi. Bu süreçte
ilahiyat ve felsefe alanındaki çalışmalarını, Gauss tarafından verilen dersler de dahil olmak üzere matematikle destekledi. İlerleyen süreçte Riemann’ın doktora tezi danışmanı yine Gauss olacaktı.

Kasım 1851’in sonlarında Riemann doktora tezini sundu. Tez, analitik fonksiyonların geometrik özelliklerinin araştırılması ile ilgiliydi. Yirmi beş yaşında sunduğu tezi bugün hâlâ karmaşık analizin başyapıtı olarak bilinir. Tezinde Riemann yüzeyleri kavramını ortaya atmıştı.

Daha sonra, Almanya üniversitelerinde ders vermek için gereken başka bir diplomayı almak amacıyla çalışmaya başladı. O diplomayı alabilmesi için Riemann’ın Habilitationsvortrag olarak adlandırılan bir deneme dersi vermesi gerekliydi.

Tüm öğrenciler gibi profesörlerine üç konu sundu. İlk ikisini eksiksiz bir şekilde araştırmıştı. Ancak geometrinin temelleri üzerine olan sonuncusunu o kadar kapsamlı bir şekilde hazırlamamıştı. Geometriye olan ilgisi nedeniyle Gauss, Riemann’ın üçüncü seçeneğini seçmesini istedi.

Sonunda 10 Haziran 1854 tarihinde, Riemann “Geometrinin Temelinde Yatan Hipotezler Üzerine” adlı konuşmasını yaptı. Dinleyiciler arasında Riemann’ın sunumunun detaylarını kavrayan tek kişi muhtemelen Gauss’tu, Riemann o sırada henüz yirmi yedi yaşındaydı.

Sonunda da övgü dolu sözler elde ederek hem sunumunu başarı ile attı, hem ders vermeye hak kazandı hem de insanlık için yeni bir adıma ön ayak oldu. Riemann’ın hemen hemen hiç denklem kullanmadan anlattığı konu, çok boyutlu bir uzayda etrafınıza baktığınızda gördüklerinizle uzayı ne kadar ve ne şekilde tanıyacağınızla ilgiliydi. Günümüzde bu konuyu Riemann geometrisi adı ile biliyoruz.

Bernhard Riemann İle Görelilik Teorisinin İlgisi Nedir?

Öklid Geometrisi, düzlem ile ilgilidir. Okullarda öğrendiğimiz geometri ile ilgili tüm kavramlar Öklid geometrisi üzerine kurgulanmıştır. Şimdi, düz bir kağıt parçası yerine, bir silindir ya da bir küre gibi eğri yüzeye sahip bir kağıdınız olduğunu varsayalım.

Bu gibi yüzeyleri incelemek düz yüzeyleri incelemekten daha zordur. Ancak yine de bu gibi yüzeylerde, bir üçgenin hipotenüsünün uzunluğunu, bir çemberin çevresini tahmin etmek için kullanılabilecek teoremler vardır. Bu tahminler, yüzeyin kavisli veya bükülmüş olduğu miktara bağlıdır. Riemann Geometrisindeki temel konulardan biri eğri yüzeylerin incelenmesidir.

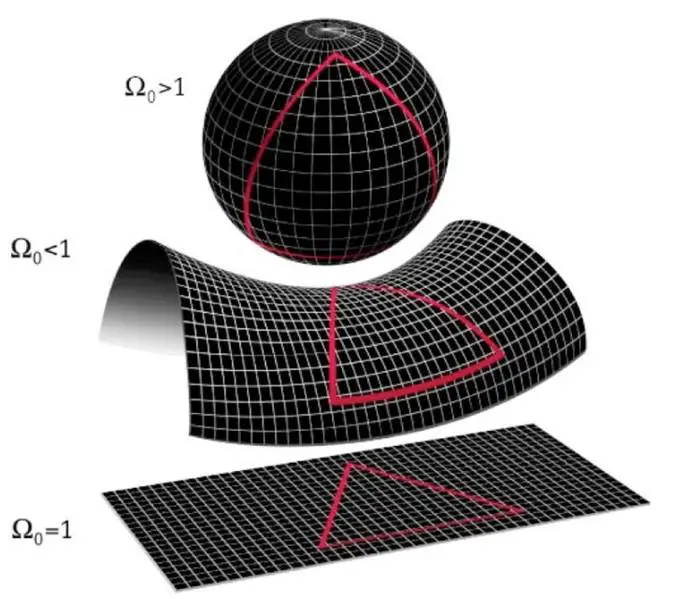
Riemann geometrisi aynı zamanda uzayların daha yüksek boyutlarının incelenmesiyle de ilgilidir. Dünya’nın yakınında evren üç boyutlu Öklid uzayına benzeyecektir. Ancak yıldızlar ve kara delikler gibi çok ağır nesnelerin yakınında uzay kavislidir. Bu nedenle ilişkiler kavisli yüzeyleri geometrisi gibi de düşünebileceğiniz Riemann geometrisi ile ilişkilidir.

Bernhard Riemann’ın Çalışmaları Olmadan Einstein Teorisini Tamamlayamazdı

Riemann’ın eğrilik tanımı, Einstein’ın genel görelilik kuramını geliştirmek için kullandığı matematiğin temel bir bileşeniydi. Bu tanım olmadan kuramının son şekline ulaşamazdı. Eğri uzay-zamanı tanımlamak için Einstein, 19. yüzyıl matematikçisi Bernhard Riemann’ın daha önceki çalışmalarına başvurdu. Ve yine bir matematikçi olan arkadaşı Marcel Grossman’ın yardımıyla Einstein, eğri uzayların matematiğini veya matematikçilerin “diferansiyel geometri” dediği şeyi öğrenmek için birkaç yorucu yıl geçirdi.

Kesin olan bir şey vardı: Einstein hayatında hiç bu kadar sıkı çalışmamıştı. 1912’de bir arkadaşına, kütleçekim problemiyle kıyaslandığında özel görelilik kuramının “çocuk oyuncağı” olduğunu yazmıştı. Ayrıca içinde matematiğe karşı yeni bir saygı doğmuştu.

Günümüzde Riemann Geometrisi diferansiyel geometrinin bir genellemesidir. Diferansiyel geometri, matematik ve Lineer Cebir kullanarak eğrilerin ve yüzeylerin geometrisini inceler. Riemann Geometrisi de bir Riemann metriği kullanarak düzgün manifoldların incelenmesini sağlar. ( Manifold matematikte topolojik bir uzaydır).

Milenyum Problemi: Riemann Hipotezi

Daha 28 yaşındayken tüm bunları başaran Riemann, üç yıl sonra bir çalışma daha yayımlayacaktı. Abelyen Fonksiyonlar Kuramı adını taşıyan bu çalışmasıyla Berlin Akademisi’ne seçildi ve Göttingen’de doçent oldu. Devamında da sayılar kuramı üzerine yazdığı ilk ve tek makaleyi kaleme aldı. Kaleme aldığı bu makalede ortaya attığı bir fikir ise günümüzde bir milenyum problemi olarak bilinmektedir.

Verilen bir sayıdan küçük kaç asal sayı olduğunu hesaplamaya yönelik bu makale, Euler’in reel sayılar için kullandığı bir fonksiyonu alıp karmaşık sayılarla yeniden hesaplamaya kalkışır. Kurduğu bu fonksiyon bugün Riemann’ın zeta fonksiyonu adı ile tanınır.

Aslında düzlemin sadece bir kısmında tanımlı olan bu fonksiyonu gamma fonksiyonu yardımıyla tüm düzleme yayar. Sonrasında da asal sayıların dağılımıyla bu fonksiyonun sıfırları arasında ilişkiler kurar. Özellikle bu fonksiyonun sıfırlarının, reel kısmı 0 ve 1 arasında olanlarının, asalların dağılımda söz sahibi olduğunu gösterir. Bir paragrafın ortasında “bu sıfırların hepsinin reel kısmı ½ gibi görünüyor. ” der. Bu sözü günümüzde matematik tarihinin çözülememiş en büyük problemidir.

Sonuç olarak;

Tüm bu şaşırtıcı keşifleri sadece 39 yıl içinde başaran Bernhard Riemann 1862’de tüberküloza yakalandı ve iyileşmek için üç kez İtalya’ya gitti. Riemann, 1866’daki üçüncü yolculuğunda 20 Temmuz 1866’da yaşamını yitirdi. Ortaya attığı kavramların günümüz matematiğin temelleri olarak kabul edilmesi nedeniyle Riemann için ilk modern matematikçi olarak kabul edilmektedir. Ancak çalışmalarının çok azı hayatta olduğu sürede yayınlandığı için kendisi hak ettiği değeri çok sonra elde edebilmiştir.

Kaynaklar ve ileri okumalar:

• Without Einstein it would have taken decades longer to understand gravity. Yayınlanma tarihi: 22 Kasım 2015. Kaynak site: Conversation. Bağlantı: Without Einstein it would have taken decades longer to understand gravity
• Bernhard Riemann, The Mind Who Laid the Foundations for Einstein’s Theory of Relativity. Yayınlanma tarihi: 23 Eylül 2020. Bağlantı: Bernhard Riemann, The Mind Who Laid the Foundations for Einstein’s Theory of Relativity

Matematiksel