Condorcet Paradoksu: Seçimin Kazanını Belirlemek Kolay Değildir!

Seçim ya da Condorcet paradoksu, çoğunluk oylamasının görünüşte paradoksal davranışlara yol açabileceği gerçeğine işaret eder.

Her türlü oylama sistemi, adaleti sorgulanabilir sorunlarla karşılaşır. Bu nedenle liderlerimizi seçmek için kullandığımız yöntemlerin hepsi mantıksızdır ve bu matematiksel bir gerçekliktir. Günümüzde seçim sistemleri bu tür problemleri çözmeye adanmış bir disiplin olan sosyal seçim teorisi kapsamında incelenir.

1700’lü yıllarda iki Fransız soylusu, çok adaylı seçimlerin nasıl organize edileceğini düşünmüştü. Bu kişiler Marqis de Condorcet ve Jean-Charles de Borda idi. Marquis de Condorcet (1743-1794), bilimin benzeri görülmemiş bir ilerleme sağlayacağına inanan bir Fransız devrimciydi. Kendisi aynı zamanda bilimsel bir modeli toplumun sosyal ve politik boyutlarına uygulamayı amaçlayan bir matematikçiydi. 

Condorcet, teorisini 1785 tarihli Essay on the application of Analysis to the Probability of Majority Decisions (Çoğunluk Kararlarının Olasılığına Analiz Uygulaması Üzerine Bir Deneme) adlı çalışmasında izah etti. Kendisi bir seçim sisteminin tutarlı olması için bazı aksiyomlara dayanması gerektiğini düşünüyordu. Bu nedenle işe temel bir aksiyom tanımlayarak başladı.

Aksiyom “Eğer seçmenlerin çoğunluğu aday A’yı aday B’ye tercih ediyorsa o zaman aday B halkın tercihi olamaz.” biçimindeydi. Bir seçimde kazananlarının birinci sırada yer alması, kaybedenlerin ise seçimde birinci sırada yer almaması gayet makul görünüyor. Bunlar sırasıyla Condorcet kazanan kriteri ve  Condorcet kaybeden kriteridir. Ne yazık ki, iki adaydan fazla olduğunda sorunlar çıkmaya başlayacaktır.

Condorcet Yöntemi İle Seçim Nasıl Yapılmaktadır?

Konuyu anlamak için  A, B ve C olmak üzere üç aday ve 30 seçmen ile gerçekleştirilen bir seçimi ele alalım. Seçim sonucu aşağıdaki gibi olsun. ( A>B dendiği zaman bir seçmenin A’yı B’ye tercih ettiğini anlamanız gerekiyor)

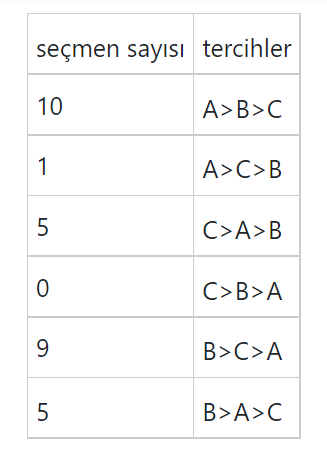
Bu seçimde A, B’yi 16 kez ve B’de A’yı 14′ kez yener. Yani A ile B yi karşılaştırdığımız zaman A iki oy öndedir. Şimdi A ile C’ye bakalım. Gördüğünüz gibi A, C’yi yine 16 kez yener. C ise, A’yı 14 kez yener, yani yine A, C’nin 2 önündedir. Şimdi de B ile C’ye bakmamız gerekiyor. B, C’yi 24 kez yener ve C’de, B’yi 6’kez yener. Bu nedenle B açık ara C’nin 18 oy önündedir. Şimdi tüm bunları bir şema ile gösterelim.

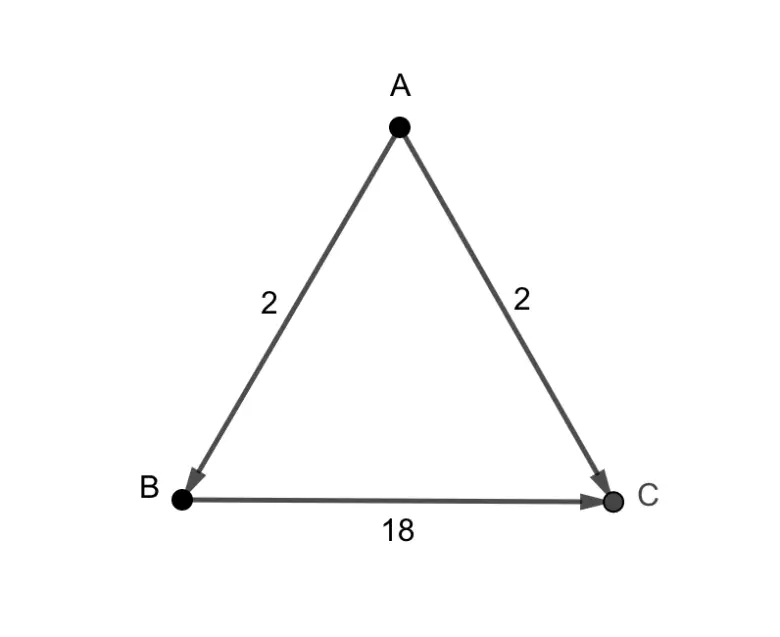
Sizin de gördüğünüz gibi bu yönteme göre seçimi kazananı yani Condorcet kazananı A olmalıdır. Ancak ne yazık ki işler her zaman bu örnekteki kadar kolay yürümez. Bu mantıkla bir kazanan bulmak kimi zaman mümkün olmaz. Bunun klasik bir örneği taş-makas-kağıt oyunudur.

Bu örnekte, taş makası yener, kağıt taşı yener ve makas kağıdı yener. Peki kim kazanır? Hiç kimse. Buna döngüsel durum denir ve Condorcet kazananı yoktur.

Condorcet ( Seçim) Paradoksu Nedir?

Şimdi biraz daha karmaşık bir seçime göz atalım. Bu seçimde 7 seçmenimiz ve dört tercih olsun. Seçim sonucunda sıralamaları aşağıda görebilirsiniz. Yanında da sonuçları bir şemada inceleyelim. Şemada örneğin B’den C’ye giden ok, B’nin C’yi 3 oy farkla mağlup ettiğini gösterir.

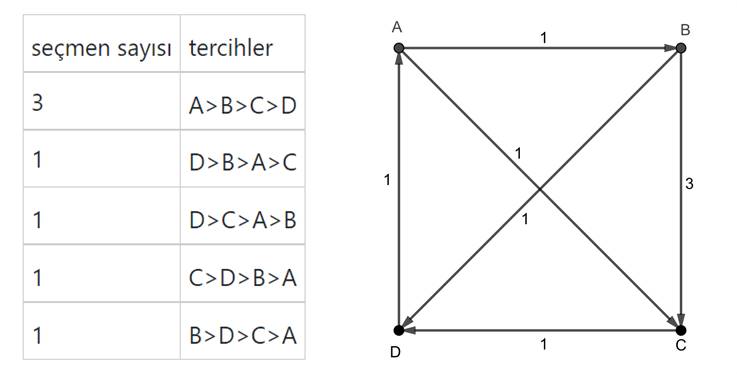
Yukarıdaki sonuçlara baktığınız zaman seçimi kazanan kişinin A olduğunu düşünmeniz olasıdır. Ancak ikili karşılaştırma yaptığınız zaman bu durum değişir. A, B’yi 4 kez ve B’de A’yı 3 kez yener. Yani A ile B yi karşılaştırdığımız zaman A bir oy öndedir.

A ile C içinde aynı sonuç geçerlidir. A ile D’yi karşılaştırdığınız zaman da D, A’yı 1 oy farkla geçecektir. B ile C’ye baktığımız zaman oy farkı 3 olur. B ile D arasında da bu fark 1’dir. Dikkat ettiyseniz ikili karşılaştırmalarda hem A hem de B iki defa kazanıyor. C ve D’de birer kez kazandı. Bu durumda Condorcet kazananı yoktur.

Üç veya daha fazla seçenek olduğunda, seçmenlerin tercihleri ​​arasında çoğunluk oylaması bir döngü oluşturacaktır. Günümüzde biz de bu duruma Condorcet paradoksu diğer adıyla seçim paradoksu diyoruz. Condorcet böyle bir durumda ne olması gerektiğini söylemedi. Onun önerisi yalnızca tek bir adayın, yani “Condorcet adayının” olduğu ve başa baş yarışta diğer tüm adayları yeneceği durumlara atıfta bulunuyordu.

Seçim Paradoksuna çözüm Var mı?

Bunun üzerine matematikçi Jean-Charles de Borda, her adaya sıralamasına göre puan veren kendi seçim yöntemini önerdi. Amacı, Fransız Bilimler Akademisi tarafından yeni üyelerin seçilmesini iyileştirmekti. Borda’nın istemi her adaya sıralamasına göre puan verme mantığına dayanıyordu.

Örneğin, beş aday varsa, Borda bir seçmenin oy pusulasında birinci sıra için adaya beş puan, ikinci sıra için dört puan vb. vermeyi öneriyordu. Ancak zaman içinde bu sisteminde bazı kusurları olduğu anlaşılacaktı.

Condorcet seçim paradoksuna bir çözüm bulamadan ölmüştü. Fransız devrimi sırasında siyasi olarak aktif bir figürdü ve Fransa anayasası taslağı hazırlamakla da meşguldü. İlerleyen süreçte hain kabul edilecek ve hapishanede yaşamını yitirecekti.

Sonraki 150 yıl boyunca düzinelerce matematikçi kendi oylama sistemlerini oluşturmaya çalıştı ya da Condorcet ile Borda seçim sistemlerine iyileştirmeler önerdi. Ancak her oylama sisteminde er ya da geç benzer sorunlar ortaya çıkıyordu.

Daha iyi veya daha adil bir sistem bulma girişimleri, 1951’de Stanford Üniversitesi’nden bir ekonomist olan Kenneth Arrow, toplam tercihler konusuna şaşırtıcı yeni bir ışık tutan bir sonuç sunana kadar yıllarca devam etti. Yazının devamında göz atmanızı öneririz: Arrow’un İmkansızlık Teoremine Göre Adaletli Bir Seçim Yoktur!

Kaynaklar ve ileri okumalar

• Elections: Could they be fairer?; yayınlanma tarihi: 14 Kasım 2019; Kaynak site: Plus Math. Bağlantı: Elections: Could they be fairer?/
• Gehrlein, William. (1997). Condorcet’s Paradox and the Condorcet Efficiency of Voting Rules. Mathematica Japonica. 45. 173-199.
• Kurrild-Klitgaard, Peter. (2001). An Empirical Example of the Condorcet Paradox of Voting in a Large Electorate. Public Choice. 107. 135-45. 10.1023/A:1010304729545.

Size Bir Mesajımız Var!

Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel