M.Ö 450 civarında Klazomenai’lı Anaksagoras’ın bolca zamanı vardı. Çünkü “Dünyayı aklın yönettiğine” inanan bu filozof, döneme göre bazı sakıncalı düşüncelerinden dolayı hapisteydi. Hapisteki boş zamanını çemberi karelemek olarak isimlendirilen antik bir matematik problemi ile uğraşarak geçirecekti.

Bilinen dünyanın belki de ilk problemlerinden biri, çemberi karelemek, yani bir işaretsiz cetvel ve pergel kullanarak daire ile aynı alana sahip bir kare elde etmektir. Bu problem kesinlikle göründüğünden çok daha zordur. 1000 parçadan oluşan daire biçiminde bir puzzle hayal edin. Şimdi tam olarak aynı parçaları kullanarak bir kare yapmaya çalışın. Puzzle parçalarının şeklinden dolayı bunun mümkün olmadığını hemen fark edeceksiniz.

Çemberi Karelemek Neden Önemlidir?
Matematik problemi çözmeye sadece günümüz matematikçilerinin takıntılı olduğunu düşünüyorsanız aslında yanılıyorsunuz. Aynı durum Antik Yunanlılar zamanında da geçerliydi. Özellikle üç problem o dönemin düşünürlerini uzun süre meşgul etmişti.
Bu problemler günümüzde antik çağın üç problemi olarak bilinmektedir. Çemberi karelemek bu problemlerden birisi idi. Problemin ilk görüldüğü yer ise hayatta kalan en eski matematiksel metinlerden biri olan Rhind papirüsü idi. Konu ile uğraşmaya başlayan ilk kişi ise başta da tanıttığımız Anaksagoras olacaktı.

Tüm çemberlerin çevrelerinin çaplarına oranının sabit bir sayı olduğu çok eski çağlardan bu yana bilinmekteydi. Bununla beraber bu sayının tam değerine ulaşmak oldukça güçtü. Bilinen ilk yazılı kaynakta çözümü aranan çemberi kareleme problemi ise bu oranı bulma yollarından bir tanesiydi.
Nitekim kare insanların ölçme adına kullandıkları en basit ve yalın araçtı. Alanını hesaplamak oldukça kolaydı. Eğer bir kare ile aynı alana sahip bir daire elde edilirse, tüm dairelerin alanını tam olarak hesaplamak mümkün olacaktı. Bu sayede de tüm çemberlerde sabit olan, Pi sayısına ulaşılacaktı. O tarihten sonra pek çok matematikçi çemberi kareleme problemi ile uğraştı.

Leonardo da Vinci’nin de çemberi kareleme problemine yönelik çalışmaları olduğu bilinmektedir. Ancak Leonardo da Vinci pergeli ve cetveli kullanarak matematiksel bir çözüme ulaşamamıştır. Bununla beraber bir çözüm iddiası ortaya atmıştır. İç içe geçmiş bir çember ve bir karenin ortasında bir erkek vücudu. Vitruvius Adamı olarak tanıdığımız bu eskiz Leonardo da Vinci tarafından yapıldı.

Çemberi Karelemek Neden Mümkün Olmadı?
Anaxagoras’ın sorduğu sorunun cevabı 1882’de Alman matematikçi Ferdinand von Lindemann tarafından verilecekti. Pi sayısının özelliklerini araştıran matematikçilerden biri olan İsviçreli matematikçi Johann Heinrich Lambert (1728-1777) ilk olarak pi’nin irrasyonel bir sayı olduğunu kanıtladı. Yani bu sayı hiçbir zaman tekrarlanan bir düzene girmeyen sonsuz sayıda rakama sahipti.
Ardından Ferdinand von Lindemann pi’nin rasyonel bir cebirsel denklemle gösterilemeyeceğini kanıtlayacaktı. Bu klasik araçlarla çemberi karelemenin mümkün olmadığı anlamına da geliyordu.
Bu hikayenin sonu gibi gelmiş olabilir ama Alfred Tarski kuralları değiştirerek sorunu yeniden canlandırdı. 1924’te Stefan Banach ve Alfred Tarski, matematiksel olarak sağlam bir kanıtını sunarak matematik camiasını şaşkına çevirdi.
Teorik olarak içi dolu bir küreyi sonlu sayıda parçalara ayırmak ve ve bunları hiç eğip bükmeden, germeden, yalnızca öteleme ve döndürme yolu ile yeniden bir araya getirdiğimizde, her biri orijinaliyle tamamen aynı boyut ve şekilde olan iki küre oluşturmak matematiksel olarak mümkündü.
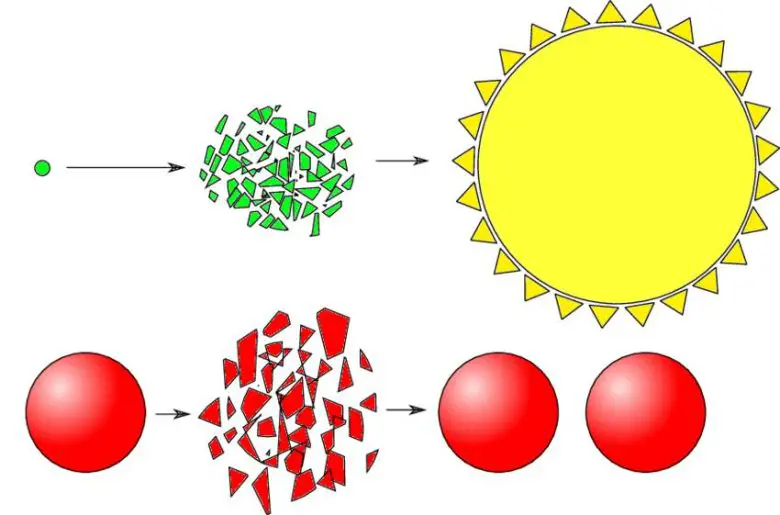
Tarski ayrıca bir daireyi alıp onu sonlu sayıda parçaya böldü ve eşit alanlı bir kare elde etmek için parçaları yeniden birleştirdi. Bunun mümkün olduğu da 1990 yılında Miklos Laczkovich tarafından kanıtlandı. Ancak bu sonuca ulaşmak için Laczkovich şekillerle çalışmadı. Bunun yerine geometri problemini bir grafik teorisi problemine dönüştürdü.
Bir sonraki büyük adım onlarca yıl sonra Ocak 2016’da Łukasz Grabowski, Máthé ve Pikhurko tarafından yayınlanan bir makaleyle geldi. Ancak yine bir sorun vardı: Çemberin parçaları ( en az 10²⁰⁰ parça kullanılmıştı) karenin tamamını hala doldurmuyordu. Çok çok küçük bir bölümünü kaplamak için hâlâ ek parçalara ihtiyaç vardı.
Şaşırtıcı bir şekilde matematikçiler bu soru üzerinde çalışmaya devam etti. Son katkı da 2022’de Warwick Üniversitesi’nden Andras Máthé ve Oleg Pikhurko ile Victoria Üniversitesi’nden Jonathan Noel tarafından yapıldı. Katkı küçük bölümü kapatacak daha fazla parça bulmakla ilgili idi.
Sonuç olarak
Çemberi karelemek bir Öklid uzayında imkansızdır. Yani Anaxagoras’ın orijinal sorusu ebediyen çözümsüz kalacaktır. Ancak aynı problem farklı geometrik yaklaşımlar ile bir çözüme sahiptir. Bir sorunun matematikçileri bunca yıldız peşinden sürüklemesi ise gerçekten etkileyicidir.
Kaynaklar ve ileri okumalar
- An Ancient Geometry Problem Falls to New Mathematical Techniques. Yayınlanma tarihi: 8 Şubat 2022. kaynak site: Quanta magazine. Bağlantı: An Ancient Geometry Problem Falls to New Mathematical Techniques
- Mathematicians Found a Way to Simplify an Ancient Greek Geometry Problem. Yayınlanma tarihi: 28 Şubat 2022. Bağlantı: Mathematicians Found a Way to Simplify an Ancient Greek Geometry Problem
- Máthé, András & Noel, Jonathan & Pikhurko, Oleg. (2022). Circle Squaring with Pieces of Small Boundary and Low Borel Complexity.
- Grabowski, Łukasz & Máthé, András & Pikhurko, Oleg. (2016). Measurable equidecompositions for group actions with an expansion property. Journal of the European Mathematical Society. 24. 10.4171/JEMS/1189.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.





