İnternetin ve akıllı telefonların ortaya çıkmasından tam bin yıl önce, İranlı bilim insanı ve çok yönlü düşünür Muhammed bin Musa el-Harezmi, algoritma kavramının temellerini attı. Aslında “algorithm” kelimesi, onun isminin Latinceleştirilmiş hâli olan algorithmiden türemiştir. Ve tahmin edilebileceği gibi, cebir anlamına gelen “algebra” kelimesiyle de yakından ilişkilidir.

Harezmi Kimdir?
El-Harezmi’nin yaklaşık 780 ile 850 yılları arasında, İslam’ın Altın Çağı olarak bilinen dönemde, bugünkü Özbekistan sınırlarında, Aral Gölü’nün güneyinde yer alan Harezm bölgesinde doğduğu düşünülüyor. Yaşadığı dönem, bilimde büyük ilerlemelerin yaşandığı Abbâsî Halifeliği dönemiyle çakışır. Ancak ne yazık ki hayatına dair çok az detay günümüze ulaşmıştır.

El-Harezmi yalnızca bir matematikçi değildi; aynı zamanda coğrafya, astronomi ve trigonometriyle de yakından ilgileniyordu. Dünya haritalarını daha doğru hale getirmek için Batlamyus’un ünlü Geographia adlı eserindeki hataları düzeltti. Güneş, Ay ve gezegenlerin hareketlerini anlamaya yönelik hesaplamalar yaptı; trigonometrik fonksiyonlar üzerine çalıştı ve tarihte bilinen ilk tanjant tablolarını hazırladı.
Bu çalışmalarının büyük bir kısmını Bağdat’taki Bilgelik Evi’nde yürüttü. Burası, farklı kültürlerden gelen bilgi ve metinlerin Arapçaya çevrildiği, sonra da bu bilgiler üzerinde yeniden düşünülerek ilerlemeler kaydedilen bir düşünce merkeziydi. Matematik de burada yalnızca bir bilim değil, kültürel bir değer haline gelmişti — ve El-Harezmi, bu hareketin kalbinde yer alıyordu.

Aryabhatta ve El Harezmi Elele: On Tabanlı Rakam Sistemi
Birçok kişi, ondalık sayı sistemini yani 10 tabanlı rakam sistemini El-Harezmi’nin geliştirdiğini sanır. Ancak bu, yaygın ama yanlış bir bilgidir. Bugün kullandığımız 0’dan 9’a kadar olan simgeleri içeren sistem, aslında “Hint-Arap rakamları” olarak bilinir. Bu sistemin adı bile kökenini açıkça ortaya koyar: Rakamlar ilk olarak Hindistan’da geliştirilmiş, ardından Arap matematikçiler tarafından alınarak Batı’ya tanıtılmıştır.

Bu sayı sisteminin temelleri, 5. yüzyılda yaşamış Hintli matematikçi Aryabhata ve onun çağdaşlarının çalışmalarına dayanır. Aryabhata, Hint matematiğinin altın çağı olarak bilinen dönemin öncülerindendir ve aynı zamanda önemli bir astronomdur.
Hint rakam sistemiyle bilinen ilk temaslardan biri, MS 773 yılında Abbâsî Halifesi Mansur’a sunulan Hint astronomi kitapları sayesinde gerçekleşti. Bu eserler, Hint matematiğinin Arap dünyasına ulaşmasında önemli bir dönüm noktasıydı. El-Harezmi de bu mirastan etkilenenler arasındaydı. Hintli matematikçi Aryabhata’nın çalışmalarını temel alarak, 820 yılında bu sistem üzerine kapsamlı bir kitap kaleme aldı.
El-Harezmi’nin bu eseri daha sonra Latince’ye çevrildi ve Avrupa’da büyük ilgi gördü. Bugün evrensel olarak kullanılan rakamların Batı’da yaygınlaşması, büyük ölçüde El-Harezmi’nin bu aracılığı sayesinde gerçekleşti.
Cebiri Harezmi mi Buldu?
Cebir, El-Harezmi’den önce de bilinen ve uygulanan bir matematik dalıydı. Ancak onun katkısı, bu bilgiyi sistemli hale getirmesi ve yazılı bir metinle kayıt altına almasıdır.

El-Harezmi, yaklaşık 830 yılında yazdığı “Kitab al-Muhtasar fi Hisab al-Cebr ve’l-Mukabele” adlı eseriyle, cebiri bağımsız bir disiplin olarak tanımlayan ve kurallarını açıklayan ilk kişi oldu. Bu eser, yalnızca matematiksel denklemleri çözmeye yönelik yöntemler sunmakla kalmadı. Aynı zamanda “cebir” (al-jabr) kelimesinin de isim babası oldu.

El-Harezmi’nin matematiksel problemleri çözme sanatı, algoritma kavramının temelini attı. Onun çalışmaları, ondalık gösterimi kullanarak dört temel işlemi (toplama, çıkarma, çarpma ve bölme) yapmaya yönelik ilk ayrıntılı açıklamaları içeriyordu.
El-Harezmi’nin matematiksel problemleri çözme sanatı, algoritma kavramının temelini attı. Onun çalışmaları, ondalık gösterimi kullanarak dört temel işlemi (toplama, çıkarma, çarpma ve bölme) yapmaya yönelik ilk ayrıntılı açıklamaları içeriyordu.
Harezmi’nin Denklem Çözme Mantığı
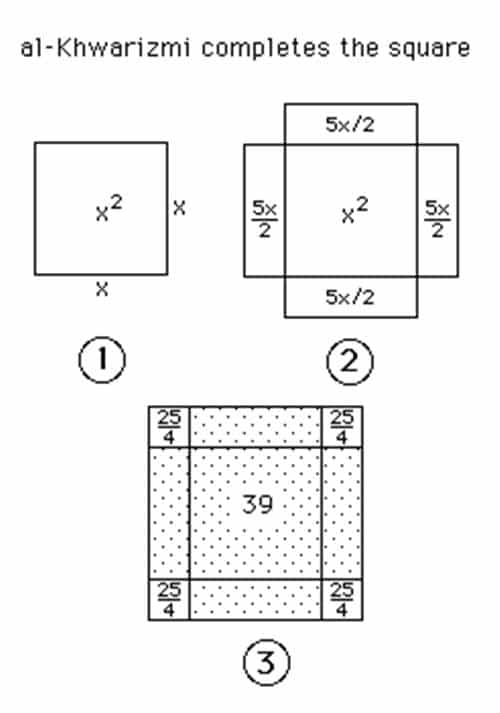
Denklemimiz x2+10x=39 olsun. Harezmi bu denklemi şu şekilde ifade ediyordu. “Hangi sayının karesi, sayının 10 katı ile toplanırsa 39 eder?” Bu ifade tarzı, o dönemin cebir anlayışını yansıtır.
Burada x2 terimi kenar uzunluğu x olan bir kareyi temsil eder. Denklemdeki +10x terimi ise kenar uzunluğunun 10 katının, karenin alanına eklendiğini gösterir. Denklemin sağ tarafındaki 39 sayısı, bu yeni şeklin yani kare ve ek dikdörtgenlerden oluşan birleşik yapının toplam alanıdır. Diğer bir deyişle, x2 +10x teriminin temsil ettiği yeni alan 39’a eşittir.
Harezmi bu noktada “tam kareye tamamlama” yöntemini kullanır. Amacı, bu birleşik şekli gerçek bir kare haline getirmek ve kenar uzunluğunu hesaplamaktır. Bunu yapmak için 10x terimiyle temsil edilen dikdörtgeni dört eşit parçaya böler. Bu parçaları, orijinal karenin dört kenarına yerleştirir.
Bu şekilde yeni bir dörtgen elde edilir. Bu dörtgen neredeyse karedir, ancak köşelerde dört küçük boşluk kalır. Köşelerdeki boşluklar, kenar uzunluğu 5/2 olan karelerdir. Bu nedenle her küçük karenin alanı, 5/2’nin karesine eşittir veya 25/4’tür. Dört küçük karenin toplam alanını bulmak için 25/4’ü 4’le çarpınca 25 çıkar.
Başlangıçta alan 39 idi. Bu küçük kareler de eklendiğinde yeni şeklin alanı 39+25=64 olur. Bu yeni şekil artık tam bir karedir ve alanı 64’tür. Karenin alanı 64 olduğuna göre, bir kenarı 8 olur.
Son adımda, Harezmi 8 sayısından iki küçük karenin kenar uzunluğunu çıkartarak, x değerini bulur. Küçük karelerin kenar uzunlukları 5/2 idi. İki küçük karenin kenarlarının toplamı, 2 çarpı 5/2 yani 5’tir. Büyük karenin kenar uzunluğu olan 8’den 5 çıkarılınca x değeri 3 olarak bulunacaktır.
Sonuç olarak
Muhammed bin Musa el-Harezmi, bugün bildiğimiz matematik ve bilgisayar biliminin gelişiminde merkezi bir rol oynamıştır.
Bir sonraki dijital teknoloji kullanımınızda – ister sosyal medya akışınızı kontrol edin, ister çevrimiçi bankacılık yapın ya da Spotify uygulamasında müzik dinleyin – tüm bunların, eski çağlarda yaşamış bir Fars bilgininin öncü çalışmalarına dayandığını hatırlayın.
Kaynaklar ve ileri okumalar:
- Why algorithms are called algorithms. Yayınlanma tarihi: 9 Temmuz 2022. Kaynak site: BBC. Bağlantı: Why algorithms are called algorithms./
- Why are algorithms called algorithms? A brief history of the Persian polymath you’ve likely never heard of. Yayınlanma tarihi: 8 Mayıs 2024. Kaynak site: Conversation. Bağlantı: Why are algorithms called algorithms? A brief history of the Persian polymath you’ve likely never heard of
- Renima, A., Tiliouine, H., Estes, R.J. (2016). The Islamic Golden Age: A Story of the Triumph of the Islamic Civilization. In: Tiliouine, H., Estes, R. (eds) The State of Social Progress of Islamic Societies. International Handbooks of Quality-of-Life. Springer, Cham. https://doi.org/10.1007/978-3-319-24774-8_2
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel