Bu 9 zor matematik problemi bir zamanlar matematikte henüz cevap bulamamış soruların arasındaydı.

Morley’nin şu sözünü hiç duymuş muydunuz? “Bir matematik problemine dalıp gitmekten daha büyük bir mutluluk yoktur.” Belki Morley’nin abartıyor olduğunu düşünebilirsiniz ancak gerçek bir matematikçinin en büyük zevki genelde matematiğin derya deniz sularında kaybolmaktır. Matematik öylesine ilginç bir bilimdir ki matematik dünyası bir problemde yıllarca takılıp kalabilir.
Daha önceki bir yazımızda matematikte halen çözülememiş problemlerden bahsetmiştik. ( Buradan okuyabilirsiniz: Henüz Kimsenin Çözemediği 11 Matematik Problemi) Şimdi ise matematikçilerin çözmek için çok çaba harcadıkları, hatta bazen on yıllarını verdikleri zor matematik problemlerinden bahsedeceğiz.
1) Diophantine (Diophantus) Denklemleri
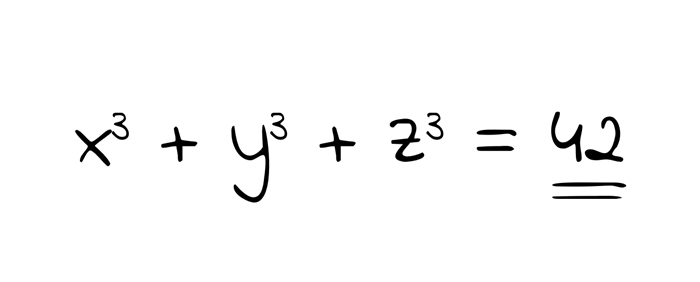
Diophantus denklemlerini kısaca üç sayının küplerinin toplamı şeklinde ifade edebiliriz. Matematiksel olarak göstermek gerekirse “x3 + y3 + z3 = k olacak şekilde bir k sayısı var mıdır?” sorusunun cevabını arıyoruz bu denklemle.
İlk başta göze çok kolay gelecektir. Örneğin x3 + y3 + z3 = 8 olacak şekilde x, y ve z sayılarını bulmayı deneyebilirsiniz. x=1, y=-1 ve z=2 olduğunda bu denklem sağlanıyor. Peki ya x3 + y3 + z3 = 42 denklemini sağlayan x, y ve z sayıları nelerdir? Bu soru matematikçileri 65 yıl boyunca uğraştırdı. Sonunda 2019 yılında bir süper bilgisayar tarafından çözüldü.
2) Poincaré Sanısı
2000 yılında Clay Matematik Enstitüsü herhangi birini bile çözene 1 milyon dolar ödül vereceğini söylediği çözülememiş yedi matematik problemini Milenyum Problemleri adıyla yayımladı. Bugün Poincaré Sanısı haricindeki diğer altı problem halen çözülmeyi bekliyor.

Henri Poincaré, 20. yüzyılda topoloji üzerinde çalışan Fransız bir matematikçiydi. Topologlar soyut şekilleri ayırt etmek için matematiksel elemanlar istiyorlardı. 3 boyutlu uzaydaki şekiller için, örneğin top ya da donut gibi, bu şekilleri sınıflandırmak zor değildi. Sonucunda top, 3 boyutlu uzayda en basit şekildi. Poincaré aynı şeyi 4 boyutlu uzay için de yapmak istedi.
Bazı revizyonlar ve geliştirmelerden sonra bu fikir “her basit bağlantılı 3-manifoldu S3 ‘te homeomorfiktir” halini aldı. Aslında bu cümle kabaca şunu demek istiyor: 4 boyutlu uzayda en basit şekil 4 boyutlu bir küreye eş değerdir.

Bir yüzyıl sonra 2003’te Rus matematikçi Grigori Perelman, modern bir açık matematik forumu olan arXiv’de Poincaré sanısını ispatladı. Yalnız Perelman’ın ispatından birtakım boşluklar vardı. Matematik dünyası Perelman’ın çalışmalarını doğrulamak için birkaç yıl harcadılar. Bu esnada Perelman’a, milyon dolarlık Milenyum Ödülü ve matematiğin Nobel’i Fields Madalyası teklif edildi. Ancak Perelman her ikisini de reddetti.
3) Fermat’ın Son Teoremi
Pierre de Fermat, 17. yüzyılda yaşamış Fransız avukat ve matematikçidir. Fermat için matematik, daha çok hobi gibiydi. İlginç bir kişiliğe de sahip olan Fermat, öldükten sonra matematikçilerin çözmek için on yıllar hatta yüzyıllar harcayacağı ispatsız iddialar ortaya atmıştı. Bunlardan en zor olanıysa, zor matematik problemi denilince akla ilk gelen, Fermat’nın son teoremi olarak bilinen teoremidir.
Yine bu teoremi de ifade etmesi oldukça basittir. a2 + b2 = c2 eşitliğini yani Pisagor üçlülerini hatırlayalım. Pisagor üçlülerini birçok x, y, z tam sayılarıyla sağlamak mümkündür. Örneğin; 92 +122 =152 ya da 72 +242 =252 eşitliklerinde olduğu gibi x, y, z tam sayıları bulmak mümkündür. Fermat bunu bir adım daha ileri götürerek x3 +y3 =z3 olacak şekilde x, y ve z tam sayılarının olduğunu iddia etmişti.

Fermat bir kitabın sayfalarından birine bu teoremini ispatladığını ancak sayfanın kenarında yeterince boşluk olmadığı için ispatını yazmadığını not etmişti. Tahmin edeceğiniz üzere matematikçileri oldukça heyecanlandıran ve meraklandıran bir nottu bu.
Yüzyıllar boyunca matematik dünyası Fermat’ın bu teoreme dair gerçekten bir kanıtının olup olmadığını merak edip durdu. Fermat’ın ölümünden 330 sene sonra 1995’te İngiliz matematikçi Sir Andrew Wiles, sonunda bu problemi çözdü. Çabalarından ötürü Kraliçe II. Elizabeth tarafından şövalye ilan edilecekti.
Wiles bu problemi çözebilmek için matematiğin çok farklı dallarını bir arada kullanacaktı. Bu konulardan birisi de eliptik eğrilerdi ki eliptik eğriler Fermat’ın yaşadığı dönemde henüz keşfedilmemişti. Bu nedenle matematikçiler Fermat’ın bu teoreme dair herhangi bir kanıtı olmadığına inanıyorlar.
4) Sonlu Basit Grupların Sınıflandırılması
Cebir grupları temelde birkaç basit özelliği (kapalılık, birleşmelilik, etkisiz eleman ve ters eleman) sağlayan kümelerdir. Bu gruplar sonlu ya da sonsuz olabilirler.
Belirli bir n boyutundaki grubun neye benzediğini bulmak için n tane seçimimiz vardır. Ancak bu oldukça karmaşık olabilmektedir. Eğer n=2 veya n=3 ise grupların yalnızca bir tek görünümü olması söz konusudur. n=4 olduğunda ise 2 farklı durum söz konusudur.

Bu durumdan ötürü matematikçiler de doğal olarak verilen herhangi büyüklükteki tüm olası gruplar için kapsamlı bir liste yapmak istediler. Bu listenin kesin olarak tamamlanması on yıllar sürdü. Çünkü listenin tamamlanmış olduğundan emin olmak hiç de kolay değildi.
1972’de Harvard’da matematikçi olan Daniel Gorenstein tarafından elde edilen sonuçlar düzenlendi. 1985’e gelindiğinde problem neredeyse çözülmüştü. Ancak çözümler çok fazlaydı ve hepsini bir araya toplamak gerekiyordu. Parça parça olsa da kanıtın birçok yönü sıkı bir incelemeden geçirilecekti. Sonrasında da kanıt 1990’lı yıllardan itibaren kabul görmeye başladı. Günümüzde de hala bu kanıt kabul görmektedir.
5) Dört Renk Teoremi
Sıradaki problemimizi de ifade etmek oldukça kolay ancak çözmesi o kadar da kolay değil. Problemimiz şu şekildedir. Size 4 bölgen oluşan bir harita veriliyor. Bu haritayı boyamanız gerekli. Ancak 4 bölgeden aynı kenarları paylaşan bölgeleri farklı renklere boyamanız gerek. Eğer denediyseniz bunun o kadar da zor olmadığını görmüş olmalısınız.
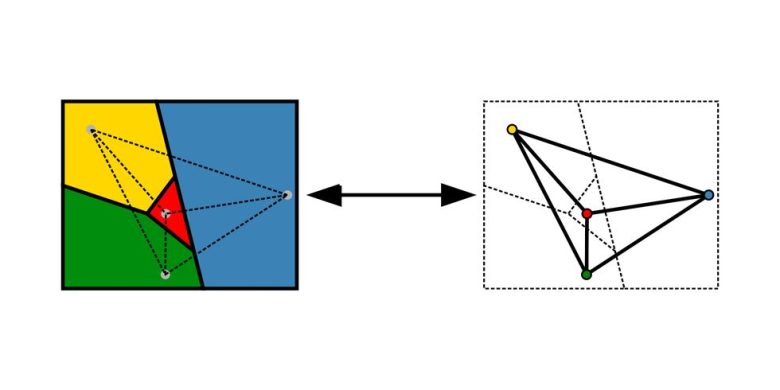
Aslında bir harita bu kurala uyularak 5 farklı renge boyamak mümkündür. 5 renk teoremi olarak bilinen bu teorem 19. yüzyılda ispatlanmış bir teoremdir. Fakat bu 5 rengi 4’e indirmek ancak 1976’da mümkün oldu. Illinois Üniversitesi’nden iki matematikçi Kenneth Appel ve Wolfgang Haken, kanıtı büyük ve sonlu bir sayıya indirmenin bir yolunu buldurlar.
Bilgisayar yardımıyla neredeyse 2000 durumu kapsamlı bir şekilde incelediler. Bu kanıt kısmen bir makinenin zihninde gerçekleştiği için tartışmalı olsa da, Appel ve Haken’in ispatı çoğu matematikçi tarafından kabul görmektedir.
6) Süreklilik Hipotezinin Bağımsızlığı
19. yüzyılın sonlarında Alman matematikçi Georg Cantor, kardinalite adında bir kavram ortaya attı. Kardinalite için kısaca bir kümenin derecesi diyebiliriz. Cantor, kardinalite hakkında temel teoremleri kanıtladı. Kanıtladığı bu teoremler günümüzde ayrık matematik (ing: discrete mathematics) konuları arasındadır.
Cantor kardinalite kavramıyla reel sayılar kümesinin kardinalitesinin doğal sayılardan daha büyük olduğu iddiasını ortaya attı. ( |ℝ|>|ℕ| –> matematiksel ifade ediliş biçimi) Peki hem reel sayılar kümesi hem de doğal sayılar kümesi sonsuzsa neden reel sayıların kardinalitesi yani sonsuzluk derecesi doğal sayılardan büyüktür diyoruz? Bir sonsuz diğer sonsuzdan nasıl daha büyük olur?
İşte bu soru bizi süreklilik hipotezine götürüyor. Eğer süreklilik hipotezi doğruysa, reel sayıların sonsuzluk boyutundan daha küçük ve doğal sayıların sonsuzluk boyutundan daha büyük bir sonsuzluk boyutuna sahip bir küme olmamalıdır. Eğer süreklilik hipotezi yanlışsa, bu iki küme arasındaki sonsuzluk boyutunda yer alan en az bir küme var olmalıdır.
Süreklilik hipotezinin matematiğin temel aksiyomlarına göre bağımsız olduğu kanıtlanmıştır. Bu şu anlama gelir. Süreklilik hipotezinin doğru olması mümkündür. Bu durumda hiçbir mantıksal çelişki içermez. Süreklilik hipotezi aynı zamanda yanlış da olabilir. Ayrıca yine hiçbir mantıksal çelişki içermez. Bu durum size oldukça tuhaf gelmiş olmalıdır. Ancak matematikte pek de nadir görülen bir olay değildir.
Bir önceki paragrafta bahsettiğimiz sonucun bulunması on yıllarca sürdü. En sonunda da iki ana bölüme ayrılacaktı. Süreklilik hipotezinin tutarlı olduğunun kanıtı ve süreklilik hipotezini reddetmenin tutarlı olmasının kanıtı. Birinci kısım Kurt Gödel sayesinde kanıtlanmıştır.
Gödel’in inşa edilebilir evreni (ing: Gödel’s Constructible Universe) olarak bilinen 1938 tarihli matematiksel yapısı, süreklilik hipotezinin temel aksiyomlarla uyumlu olduğunu kanıtlamıştır. İkinci kısım ise Stanford’da bir matematikçi olan Paul Cohen tarafından ispatlanmıştır. Cohen, model teorisinde “zorlama” (ing: forcing) olarak bilinen yöntemini icat ederek bu ispatı gerçekleştirmiştir.
7) Gödel’in Eksiklik Teoremi

Gödel, matematiksel mantık konusunda gerçekten devrim yapmış bir matematikçiydi. Bir şeyleri kanıtlamanın yanı sıra o şeylerin kanıtlanabilir olup olmadığını da kanıtlamayı seviyordu. 25 yaşındayken ortaya attığı ilk eksiklik teoremi temelde şunu söylemektedir. Herhangi bir ispat dilinde illaki ispat edilemeyen durumlar vardır. Daima doğru olan ancak doğru olduğunu kanıtlayamayacağımız doğrular vardır.
Dikkatli bir akıl yürütmeyle Gödel’in bu ifadesini anlamak pekala mümkündür. Eksiklik teoremini daha iyi anlamak için bir örnek üzerinden gidelim. “Bu ifadenin doğruluğu kanıtlanamaz.” ifadesini düşünelim. Eğer bu ifade yanlışsa kendisinin yanlış olduğunu söylediği için aslında doğru bir ifadedir. Burada bir çelişki elde etmiş olduk. Çünkü ilk başta ifadenin yanlış olduğundan yola çıktık. Fakat sonuç olarak ifadenin doğru bir ifade olduğunu bulduk. Dolayısıyla bu durum imkansızdır.
Olaya diğer taraftan bakacak olursak eğer “Bu ifadenin doğruluğu kanıtlanamaz.” ifadesinin bir ispatı varsa o zaman bu ispat onun doğru olduğunu kanıtlamalıdır. (Çünkü ifade, doğruluğunun kanıtlanamayacağını iddia ediyor.) Hiçbir kanıtı olmadığını doğrulamak da çelişki olduğundan bu durum da imkansızdır. Dolayısıyla verilen bu ifadenin doğru ancak kanıtlanamayan bir ifade olduğuyla karşı karşıya kalmış olduk.
Gödel’in ikinci eksiklik teoremi de birinciye benzer şekilde gariptir. Bu teorem ise şöyle demektedir: Matematiksel “formal sistemler” kendilerini tutarlı bir şekilde kanıtlayamazlar. Tutarlı bir şekilde kanıtlamak demek kanıtın hiçbir mantıksal çelişki içermemesi demektir. Yine bu teoremi de bir örnekle açıklayalım.
Aslı ve Banu’nun her birinin zihninde kendilerine ait bir dizi matematiksel aksiyom olduğunu hayal edelim. Eğer Aslı, Banu’nun aksiyom sisteminin çelişkisiz olduğunu kanıtlamak için kendi aksiyom sistemini kullanırsa o zaman aynı şeyi Banu da yapar. Hem Aslı hem de Banu birbirlerinin aksiyom sisteminin çelişkisiz olduğunu ispatlamak için kendi aksiyomlarını kullandıklarından çelişkiye düşerler. Matematikçiler bu sebepten ötürü matematiğin temel aksiyomlarını seçerken bu fenomeni daima göz önünde bulundurmak durumundadırlar.
8) Asal Sayı Teoremi
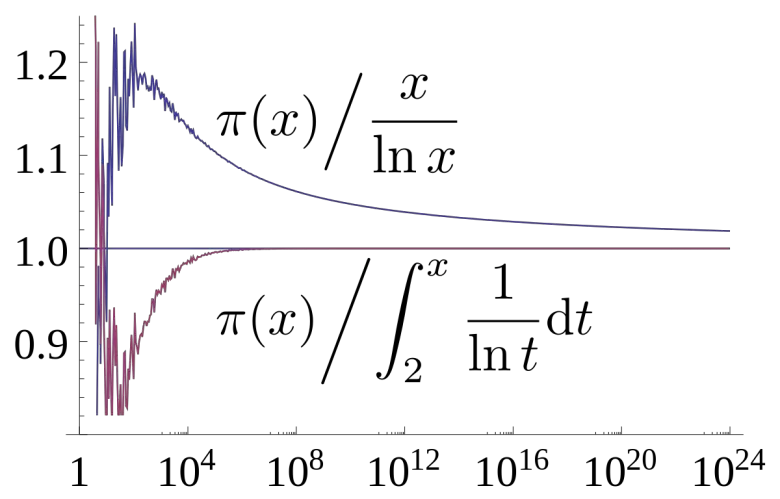
19. yüzyılda iki matematikçi olan Jaques Hadamard ve Charles Jean de la Vallée Pousin, birbirlerinden habersiz bir şekilde asal sayı teoremini kanıtlamıştır. O zamandan bu yana bu teorem birçok kez düzenlenmiştir. Bu teoremde asal sayılar sayı doğrusuna dağıtılarak tanımlanır. Başka bir deyişle bir N doğal sayısı verildiğinde bu doğal sayıdan küçük olan asal sayını yaklaşık değeri N/ log(N) ile bulunabilmektedir.
9) Polinomların Radikallerle Çözülmesi
Şimdi de lise matematik derslerinden polinom bilgilerimizi hatırlayalım. Verilen bir ax2 +bx +c=0 denkleminin çözümünü x=(-b±√(b2-4ac))/(2a) formülüyle bulabiliyorduk. Ayrıca ax3 +bx2 +cx +d=0 denklemini düşünecek olursak yine x’i bulabiliriz ancak uğraştırıcı olur. Yine aynı şekilde 4. dereceden polinomlarda da x’i bulmak mümkündür. Ancak fazlasıyla uğraştırıcıdır.
Bu tarz denklemlerin çözümüne yönelik araştırmalar 15. yüzyılda başlamıştı. 5. dereceden itibaren diğer denklemler için kapalı bir form mümkün değil gibi görünüyordu. Peki matematikçiler sizce bu durumun üstesinden nasıl gelmiş olabilirler?

Bu konuda fikir ortaya atan bilim insanlarından birisi de Galois’ti. Galois’in fikirlerinin anlaşılması ise baya zaman almıştı. Galois teoremine göre bir polinomun ne zaman radikaller tarafından çözüleceği konusunda kesin koşullar verilir. Yani ikinci dereceden bir polinomda olduğu gibi kapalı bir form bulunur. Dördüncü dereceye kadar olan tüm polinomlar bu koşulu sağlamasına rağmen beşinci dereceden itibaren her denklem bu durumu sağlamadığı için genel bir formdan söz etmek mümkün değildir.
Sonuç Olarak;
İncelediğimiz bu 9 zor matematik problemi bir zamanlar matematikte henüz cevap bulamamış soruların arasındaydı. Halen bir dolu çözülememiş problem bulunmaktadır. Ancak matematiğin güzelliklerinden birisi de budur. Her problem için bir cevap vardır, o cevabın bulunması yüzyıllar sürse bile.
Kaynaklar ve İleri Okumalar
- These Are the 10 Hardest Math Problems Ever Solved. Yayınlanma tarihi: 28 Kasım 2022. Bağlantı : The 10 Hardest Math Problems That Were Ever Solved (popularmechanics.com)
Matematiksel








