Yeni yollar inşa etmek, trafik sıkışıklığını artırır. Buna karşılık, bazı yolları kapatmak trafiği azaltır. Sezgilerimize tamamen aykırı gelen bu durum, araştırmalarla defalarca doğrulandı ve bugün Braess Paradoksu olarak biliniyor.

22 Nisan 1990 Dünya Günü’nde, dünyanın birçok yerinde çevre etkinlikleri düzenleniyordu. New York’ta Ulaştırma Komiseri Lucius J. Riccio, günü anmak için 42. Cadde’yi trafiğe kapattı. Burası kentin en yoğun yollarından biriydi. Sürücüler kararın yolculuk sürelerini felakete sürükleyeceğini düşündü. Kent, büyük bir trafik krizine hazırlanıyordu. Ancak beklentiler boşa çıktı. 42. Cadde kapatıldıktan sonra trafik sıkışıklığı azaldı.
Braess paradoksu, yeni yolların her zaman trafiği rahatlatmadığını gösterir. Uygun koşullarda yol eklemek, yolculukları daha da kötüleştirebilir. Paradoks tersine de çalışır. Bir yol kapatıldığında trafik iyileşebilir. New York’ta 42. Cadde’nin kapatılması bunun somut bir örneğidir. Buna rağmen çok az kent bu fikri planlamaya dâhil eder.

Kentler karmaşık yapılardır; yüzlerce, hatta binlerce yol kavşaklar ve dönüşlerle birbirine bağlanır. Bu yapı, trafiği incelemeyi zorlaştırır. Buna rağmen Braess paradoksunu görmek için çok sayıda yola gerek yoktur. Beş yol yeterlidir. Biraz dikkat ve sakin düşünme çoğu zaman sorunu açığa çıkarır. Yol matematiğiyle uğraşanların dediği gibi, derin bir nefes alıp Braess’e bakmak gerekir.
Braess Paradoksu Nedir?
Başlangıç ve Bitiş olarak adlandırılan iki büyük şehir olduğunu varsayalım. Bu iki şehir arasında yolculuk eden sürücüler iki rota arasından seçim yapar. Araçlar ya A Kasabası üzerinden ya da B Kasabası üzerinden ilerler.
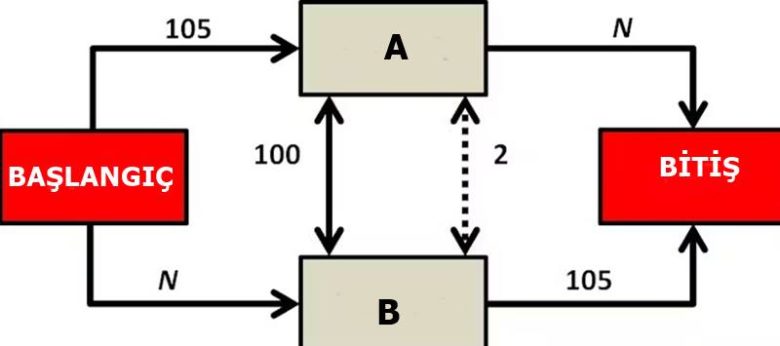
Başlangıçtan A Kasabası’na giden yol ile B Kasabası’ndan Bitiş’e ulaşan yol otoyoldur. Bu yollarda kaç araç bulunursa bulunsun, yolculuk süresi her zaman 105 dakikadır. Buna karşılık Başlangıçtan B Kasabası’na ve A Kasabası’ndan Bitiş’e giden yollar dar ve tek şeritlidir. Bu yollarda yolculuk süresi, yolda bulunan araç sayısına bağlıdır. Eğer yolda N araç varsa, her bir araç için yolculuk süresi N dakika olur.
A Kasabası ile B Kasabası’nı bağlayan, yolculuk süresi 100 dakika olan eski bir yol da bulunsun. Bu yol o kadar yavaştır ki, tek başına düşünüldüğünde hiçbir sürücü başlangıçtan bitişe giderken bu yolu içeren bir rotayı tercih etmez.
Başlangıçtan bitişe aynı anda 100 aracın seyahat ettiğini varsayalım. Bu durumda sürücüler için A ya da B Kasabası’ndan geçmek arasında belirgin bir fark kalmaz. Sonuçta tüm araçlar trafikte yaklaşık aynı süreyi harcar.
Bu koşullarda trafik iki rota arasında kabaca eşit biçimde dağılacaktır. Ağdaki ortalama yolculuk süresi yaklaşık 155 dakikadır. Şimdi A Kasabası ile B Kasabası arasındaki yolun iyileştirildiğini varsayalım. Bu iyileştirme sonucunda iki kasaba arasındaki yolculuk süresi 100 dakikadan 2 dakikaya düşsün. Bu durumda en hızlı rota değişir.
Artık tüm sürücüler başlangıçtan B Kasabası’na 100 dakikada gider. Ardından B Kasabası’ndan A Kasabası’na 2 dakikalık kısa yolu kullanır. Son olarak A Kasabası’ndan bitiş noktasına 100 dakikada ulaşır. Bu güzergâh toplamda 202 dakika sürer. Ancak bu sonuç, ilk duruma göre 47 dakika daha uzundur.
Braess Paradoksu İle İlgili Örnekler
A Kasabası ile B Kasabası arasındaki eski yol oldukça verimsizdi. Ancak bu verimsizlik, ağın genelinin makul ölçüde verimli kalmasına katkı sağlıyordu. Yol, trafiğin iki rota arasında dengeli biçimde dağılmasına yardımcı oluyordu.
Ne var ki, bu görece önemsiz yol iyileştirildiğinde, trafik artık eşit dağılmadı. Sürücüler aynı rotayı tercih etmeye başladı. Sonuç olarak, sistemin geneli iyileşmek bir yana, daha da kötüleşti.
Bu durum yalnızca basit bir matematiksel tuhaflık değildir. Yeni yollar inşa etmek yerine bazı yolların kaldırılmasının ulaşım ağlarını iyileştirdiğine dair pek çok somut örnek bulunmaktadır.

1960’ların sonlarında Stuttgart şehri, şehir merkezindeki trafiği hafifletmek amacıyla yeni bir cadde açmaya karar verdi. Ancak bu yeni yol, trafiği iyileştirmek yerine daha da kötüleştirdi ve yetkililer kısa süre sonra caddeyi kapatmak zorunda kaldı.
Yakın zamanda yapılan deneysel bir çalışma da bu durumu doğruladı: Yol kapasitesinin artırılması, bazı durumlarda trafik koşullarının herkes için daha da kötüleşmesine neden olabiliyor. Bu da, Braess Paradoksu’nun günümüzde hâlâ geçerliliğini koruduğunu gösteriyor.
Sonuç olarak
Braess Paradoksu yalnızca trafik sistemlerinde görülmez; pek çok farklı alanda da karşımıza çıkar. Örneğin, 2012 yılında Max Planck Enstitüsü’nden bilim insanları, bir enerji şebekesine yeni güç hatları eklediklerinde, sistemin performansının her zaman artmadığını gösterdi. Yeni hatlar, konumlarına bağlı olarak sistemi daha verimsiz hâle getirdi. Bazı durumlarda, daha az sayıda hat kullanmak, daha verimli bir elektrik şebekesi oluşturdu.
Benzer bir etki sporda da ortaya çıkar. Bazen bir basketbol takımının en iyi oyuncusunun çıkarılması, takımın genel performansını artırır. Braess’e göre serbest piyasalarda da aynı sorun gözlenir. Bir satıcı ürünü diğerlerinden daha ucuza sattığında başlangıçta daha fazla kazanır. Ancak rakipler fiyatları düşürdüğünde, sonunda herkesin toplam kârı azalır.
Trafikte bunaldığınız zamanlarda daha fazla değil, daha az yola ihtiyacınız olduğunu anımsayın. Bu paradoksun nedeninin bencilce hareket eden sürücüler olduğunu unutmayın. Aslında bu durum ekonomide de kendine bir yer edinmiştir.
Kaynaklar ve ileri okumalar için:
- Raphael Rosen; From Klein Bottles to Chaos Theory, a Guide to the Nerdiest Math Facts, Theorems, and Equations; 2015
- Noland, Robert & Goodwin, Phil. (2003). Building new roads really does create extra traffic: A response to Prakash et al. Applied Economics. 35. 1451-1457. 10.1080/0003684032000089872.
- Want less traffic? Build fewer roads!; Yayınlanma tarihi: 3 Eylül 2015; Kaynak site: Plus Maths. Bağlantı: Want less traffic? Build fewer roads/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





