George Boole yoksul bir kunduracının üstün zekalı oğluydu. Ekonomik zorluklar nedeniyle ilkokuldan sonra ne öğrendiyse kendi kendine öğrendi. Ancak çalışmaları sonucunda geliştirdiği Boole cebiri günümüz bilgisayarlarının ve cep telefonlarının temelini atacaktı.

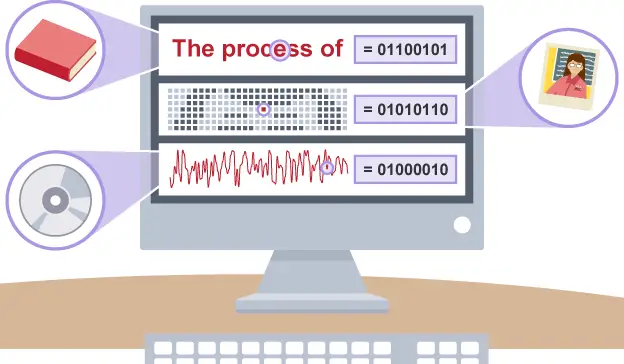
Bilgisayarlar, kelimeleri veya sayıları bizim gibi anlayamazlar. Karmaşık verileri anlamak için, bilgisayarınızın bunları ikili olarak kodlaması gerekir. Bunun başlıca nedeni, ikili aritmetiğin çarpım tablosunun ondalık sistemden çok daha basit olmasıdır.
Programlar, bilgisayarın çalışması ve belli komutları yerine getirmesi için insanlar tarafından oluşturulan mantık algoritmalarıdır. Programlardaki komut dizileri, ikili sayı sistemine göre kodlanırlar. Bu ikili sistem mantık devrelerinde 0=yanlış, 1=doğru, ya da bir elektrik devresinde 0=elektrik akımı yok, 1=akım var anlamına gelir.
Boole Cebiri Nedir?
Aşağıda bir elektrik devresine bağlı bir ampul görüyorsunuz. Ucunda da bir açma kapama anahtarı var. Anahtar kapalı olursa devre tamamlanır ve ışık yanar. Bunu sadece bir düğmeye basarak sağlamamız mümkündür.

Ancak iki anahtara bağlı bir devre kullanırsak işler ilginçleşir. Aşağıda gördüğünüz ilk devrede ışık sadece her iki geçit kapalı ise yanar. Diğerinde ise iki kapıdan en az biri kapalı olmak zorundadır. Şimdi işi kolaylaştıralım. Geçidin kapalı olması durumuna bir, açık olması durumuna da sıfır yazalım. Bu durumda karşımıza dört olasılık çıkar. Bu olasılıkları aşağıda görebilirsiniz.

| Birinci Devre | ||||
|---|---|---|---|---|
| 1. Kapı | 1 | 1 | 0 | 0 |
| 2. Kapı | 1 | 0 | 1 | 0 |
| Işık | 1 | 0 | 0 | 0 |
| İkinci Devre | ||||
|---|---|---|---|---|
| 1. Kapı | 1 | 1 | 0 | 0 |
| 2. Kapı | 1 | 0 | 1 | 0 |
| Işık | 1 | 1 | 1 | 0 |
Yukarıda gördüğünüz iki tablo bizlerin mantık dersinde öğrendiği VE ile VEYA bağlaçları için yaptığımız tablolar ile aynıdır. İlk tablo VE bağlacını göstermektedir. İkincisi ise VEYA. Matematik için ve, veya, değil ifadeleri çok önemlidir. Çünkü bunlar Boole cebrine yol açan matematiksel mantığın temelidir.

İlerleyen süreçte Boole, matematiksel olarak ele alınabilmeleri için mantıksal argümanları çerçevelemenin bir yolunu keşfetmek istedi. Bunu başarmak için bir tür dilsel cebir geliştirdi. Toplama ve çarpma gibi işlemleri mantıkta kullanılan bağlaçlar ile değiştirdi. Boole’un sembolleri ve bağlaçları kullanması, mantıksal ifadelerin basitleştirilmesine izin verdi.
“Ve” “Veya” “Değil”
Boole cebirinin üç temel işlemi VE, VEYA ve DEĞİL idi. Boole, temel matematiksel işlevlerin yanı sıra küme karşılaştırmalarını gerçekleştirmek için gerekli olan tek işlemlerin bunlar olduğuna inanıyordu. Örneğin, mantıkta, “bu hayvanın tüyleri var” VE “bu hayvan yavrusunu sütle besliyor” gibi iki ifade VE ile bağlanabilir.
A VE B ifadesi, A ve B’nin her ikisi de bireysel olarak doğru olduğunda doğrudur. “Bu hayvan yüzebilir” VEYA “bu hayvanın tüyleri var” biçiminde de bir cümle kurabiliriz. “A VEYA B” ifadesi, A ve B’den biri veya her ikisi de doğruysa doğrudur.
Boole sayıların cebirsel özelliklerini incelemiş ve {0, 1} kümesinin toplama ve çarpma gibi işlemlerle birlikte tutarlı bir cebirsel dil oluşturmak için kullanılabileceğini fark etmişti. 1854’te düşüncelerini yayınladı. Boole’un mantıksal cebirinde, doğruluk ve yanlışlık ikili değerlere indirgendi: doğru için 1 ve yanlış için 0.
Benzerliğe rağmen, Boole’un 1 ve 0’ın doğru ve yanlış ikilisi ikili sayılarla aynı değildir. Boole cebirinin “yasaları”, diğer cebir biçimleri tarafından izin verilmeyen ifadelere izin verir. Ayrıca Boole cebrinde çıkarma ve bölme diye bir şey de yoktur.
Bu cebirde VEYA toplama işlemi (1 + 1 = 1 dışında), VE ise çarpma işlemi gibi davranır. Boole cebirini görselleştirmenin bir yolu, İngiliz mantıkçı John Venn tarafından icat edilen hepimizin yakından tanıdığı Venn şemalarıdır.

Boole cebrini göstermenin en kolay yolu, olası tüm girdi kombinasyonlarının denendiği ve yazıldığı bir doğruluk tablosu yapmaktır. Bu doğruluk tabloları ilk olarak Amerikalı mantıkçı Charles Saunders Peirce tarafından 1893’te, Boole’un ölümünden yaklaşık 30 yıl sonra kullanıldı. Doğruluk tabloları çizerek daha karmaşık ifadeleri değerlendirmek de mümkün oldu.
Boole Cebiri Bilgisayar Çağını Başlattı
Boole cebiri günümüzde olasılıklar kuramı, kümeler ve bilişim için son derecede değerlidir. Ayrıca, elektronik sayısal bilgisayarlarda kullanılan devrelerin tasarımı için gerekli olan temeli oluşturmaktadır. Sizin de tahmin edebileceğiniz gibi bilgisayar çağını başlatan da Boole cebiri olmuştur.

Boole’un ölümünden yaklaşık 70 yıl sonra fikirlerinin potansiyeli önemi anlaşıldı. Bu Amerikalı mühendis Claude Shannon, adında yirmi bir yaşında bir gencin lisansüstü tezinde Boole cebirinin elektrikli sistemlerde nasıl kolaylıklar yaratacağını anlatmasıyla oldu. “Röle ve Anahtar Devrelerin Sembolik bir Analizi” adlı tezi 1938 yılında basıldığında yirminci yüzyılda insanlığın ne yöne gideceğini erkenden ilan ediyordu.
Günümüzde bilgisayar yazılımlarını programlamak için kullanılan kodların yapı taşları, Boole tarafından formüle edilen mantığa dayanmaktadır. Boole mantığı aynı zamanda internet arama motorlarının nasıl çalıştığının merkezinde yer alır. İnternetin ilk zamanlarında, VE, VEYA ve DEĞİL komutları, aranan belirli şeyi bulmak için sonuçları filtrelemede yaygın olarak kullanılıyordu.
Ancak teknolojideki gelişmeler, günümüzde insanların daha doğal bir dil kullanarak arama yapmasına olanak tanıyor. Ancak arka planda hala aynı sistem çalışıyor. Örneğin “George Boole” için yapılan bir arama, iki kelime arasında görünmeyen bir VE konutu içeriyor. Böylece sonuçlarda yalnızca her iki adı da içeren web sayfaları ekranımıza yansıyor.
Kaynaklar ve ileri okumalar:
- This Simple Math Concept Went Nowhere For A Century And Then — BOOM — Computers; https://www.businessinsider.com
- Alfred S. Posamentier and Christian Spreitzer; Math Makers; Prometheus Books
- George Boole and the wonderful world of 0s and 1s. Yayınlanma tarihi: 26 Ekim 2015; Bağlantı: https://plus.maths.org/content/george-boole
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





