Hangi mecrayı tercih ederseniz edin, sosyal medya akışınızda ” Bu matematik problemi tüm interneti etkiliyor” veya “ 10 kişiden 9’u bu soruyu çözemiyor. Cevabı biliyor musun?” biçiminden viral matematik soruları ile karşılaşmışsınızdır.

Aslına bakarsanız bu tarz sorular gerçekten de sosyal medya etkileşimi almak adına idealdir. Sonucunda soru çok kolaydır. Bir bakışta doğru cevabı bulduğunuzu düşünürsünüz. Ancak yorumlar kısmına baktığınız zaman kafanız karışır.
Yalnızca bazı insanların cevabınız ile aynı fikirde olduğunu, diğerlerinin ise tamamen farklı bir cevap verdiğini görürsünüz. Sonrasında da sonu asla gelmeyecek gibi gözüken bir tartışma başlar. Herkes karşı tarafa kendi çözüm yolunu anlatmaya çalışır. Bir örnek mi? En iyi bilinen viral matematik sorusu aşağıdadır.
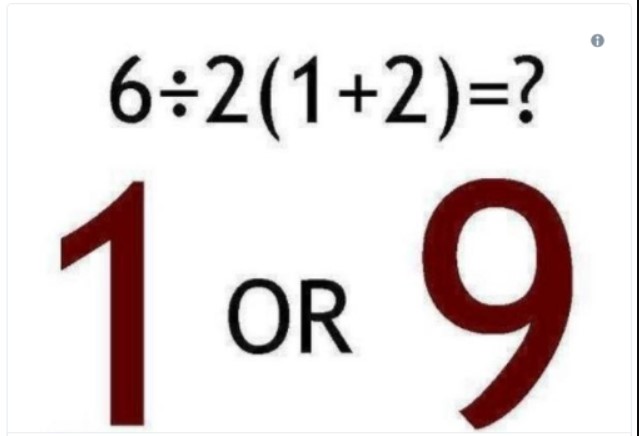
Özellikle farklı ülkelerden kişiler bu tarz tartışmalara dahil olduğunda da işler daha da karışacaktır. Peki ama neden? Cevabını bulmak için gelin önce matematiğin dilini anlamaya çalışalım.
Matematiğin de Kendine Has Bir Dili Vardır
Türkçe, İngilizce ya da Almanca. Bu dillerin hepsini soldan sağa doğru okuyoruz. Bu nedenle matematiksel denklemlere de aynı şekilde bakmak bize çok doğal görünecektir. Ancak Mandarin dilini veya Arapçayı bu şekilde okumaya çalışmazsınız. Bu nedenle bu kabulü matematik için de yapmamalısınız.
Matematik okuryazarı olmak için matematikte “imla” ve “gramer” ile ilgili kuralları anlamak önemlidir. İşlem sırası olarak bilinen katı kurallar dizisi, doğru aritmetik dilbilgisini tanımlar. Bu kurallar bize, her ikisi de bir denklemde göründüğünde, toplama ve çarpma gibi matematiksel işlemleri gerçekleştirmemiz için gereken sırayı söyler.
Bunun için farklı ülkelerde farklı anımsatıcılar kullanılmaktadır. Örneğin İngilizce konuşan ülkeler genellikle BODMAS ( Brackets – Order – Division – Multiplication – Addition – Subtraction / Parantez, üstler, bölme, çarpma, toplama, çıkarma ) biçiminde ezberler. ( Türkçe ‘de böyle bir kısaltma olmaması aslında bizim için bir avantajdır. Ancak yabancı dilde eğitim veren bir okulda okuduysanız siz de bu kısaltmalardan birini muhtemel öğrenmişsinizdir.)
Bunun sonucunda bir işlemde hem toplama hem de çarpma varsa, yazılma sırasına bakılmaksızın her zaman önce çarpma işlemini gerçekleştirmemiz gerektiğini anlarız. Şimdi aşağıdaki işlemlere bakalım.
- (a) 3×4+2
- (b) 2+3×4
Doğru işlem sırasını uyguladığımızda, bu işlemlerin aynı sonucu verdiğini görebiliriz. Sonucunda her iki durumda da 3×4=12’yi hesaplayarak işe başlarız. Sonrasında da 12+2=14 cevabını buluruz. Ancak bazı insanlar ikinci denklemi soldan sağa doğru çözmeye çalışacakları için muhtemelen yanlış cevaba ulaşacaklardır. Önce toplama (2+3=5) sonra çarpma (5×4) yaparak 20 yanlış cevabını elde edeceklerdir.

Doğru Cevap için Parantezler Fark Yaratır
Parantezlerin kullanılması gereken yer burasıdır. Sonuçta bir dilde virgülü nereye yerleştirdiğimiz cümlenin anlamını etkiler. Aynı şey matematik için de geçerlidir. Fazladan parantezler belirsizliği ortadan kaldırır ve bu sayede sorumuz iyi tanımlanmış olur.
Parantezler bir işlemin belirli bir kısmına öncelik vermemiz gerektiği anlamına gelir. Bu nedenle önce dışarıda ne olduğuna bakmadan önce parantez içini hesaplayarak işe başlarız. Yukarıdaki (a) ve (b) işlemlerindeki toplamayı köşeli parantez içine alırsak, iki yeni işlemimiz olur:
- (c) 3×(4+2)
- (d) (2+3)×4
Bu işlemler artık birbirine eşdeğer değildir. Her iki durumda da parantezler, çarpmayı yapmadan önce toplamayı yapmamızı söyler. Bu, (c) için 3×6 ve (d) için 5×4 cevabını bulmamız gerektiği anlamına gelir. Bu nedenle kafa karışıklığını önlemek için parantez eklemek her zaman işe yarayacaktır.
Matematiğin Değişme Özelliğini de Anlamamız Gerekir
İlkokul sıralarında öğrendiğimiz değişme özelliği bize toplama ve çarpmanın değişme özelliği olduğunu ancak çıkarma ve bölmenin olmadığını söyler. Yani toplama için a+b=b+a her zaman doğrudur. Aslında buna benzer bir durum dilimizde de vardır. Sonucunda “ekmek ve peynir” ile “peynir ve ekmek” aynı şeydir. Ancak “ekmeğe peynir sür” ile “peynire ekmek sür” aynı şey değildir.
Bu nedenle toplama ve çarpma bu özelliğe sahipken, çıkarma ve bölmede yoktur. Bu durumda a + b + c denklemine sahipsek, onu (a + b) + c veya a + (b + c) olarak çözmemizin bir önemi yoktur.
Ama eğer a – b – c’ye sahipsek, o zaman sıralama önemlidir. Çünkü (a – b) – c ile a – (b – c) ile aynı değildir ve her zaman soldan sağa doğru çalışmamız gerekir. Aynı biçimde, Eğer toplama ve çıkarma işlemleri yan yana ise, aralarında başka bir işlem yoksa, yine soldan sağa doğru işlem yapmalıyız. Aşağıdaki örneklere bakalım.
- (3-2)-1=0
- 3-(2-1)=2
Gördüğünüz gibi matematik bir dildir. Matematik, herhangi bir gerçek dil gibi, bir gramere ve kelimelere sahiptir. Her ikisine de yeterince aşina olduğunuzda, matematiği anlamaya başlayabilirsiniz. Matematiğin dilini kavradığınızda herhangi bir iyi tanımlanmış aritmetik işlemini çözmek için gerekli donanıma sahip olursunuz.
Peki Baştaki Sorunun Cevabı Nedir?
Baştaki sorunun cevabını kimileri 1 ve kimileri 9 olarak verecektir. Ve her iki cevap da gerçekten yanlış değildir. İşleme bir daha bakalım. 6÷2(1+2)=? Parantez içindeki toplamayı yaptıktan sonra 6÷2(3) kalıyor. Bazı insanlar, Google’ın hesap makinesinin verdiği cevap olan, 6÷2=3’ü hesaplayıp ardından 3×3=9’u çarparak soldan sağa doğru çalışmamız gerektiğini savunacaktır.
Diğerleri 2(1+2)’nin önce bütün olarak hesaplanması gerektiğini, çünkü bu terimlerin x işareti olmadan yan yana dizilmesi onun tek bir öğeden oluştuğunu ima etiğini söyleyecektir. Ancak sadece ilgi çekmek amacı ile değil de bir matematik sorusu sormak amacıyla sorulsaydı asıl soru aşağıdaki gibi olmalıydı.
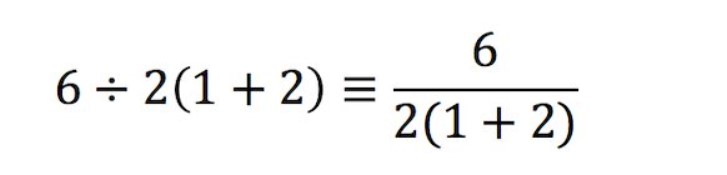
Bu durumda da cevabın kolayca 6÷6=1 olduğunu herkes görecekti. Buradaki asıl sorun bölme işaretidir. Matematikçiler (÷) bu işareti (veya çarpım işaretini ×) nadiren kullanırlar. Pratikte, kesirler gibi açık, net gösterimler kullanmayı tercih ederler.
Yukarıdaki ilk anlamı iletmek istiyorsak, denklemi (6/2)(1+2) olarak yazmak daha uygun olacaktır. Bu durumda cevap 9 olacaktır. Eğer sonucun 1 çıkmasını istiyorsak bu sefer de 6 /(2(1+2)) biçiminde yazabilirdik. Bu sayede de tüm tartışmayı ortadan kaldırabilirdik.
Çevrimiçi bulmacalar, matematiksel becerilerinizi tazelemenin harika bir yolu olabilir, ancak kasten kafa karıştıran bulmacalara dikkat etmek önemlidir. Bir daha benzer bir soru ile karşılaştığınızda önerilerimizi hatırlayabilirsiniz. Ancak cevap hala net değilse, tartışmadan kaçınmak ve bunun yerine geri adım atmak, derin bir nefes almak ve bunu doğru yazmamışlar demek daha akılcı bir çözüm olacaktır.
Kaynak ve ileri okumalar: Your guide to solving the next online viral maths problem. Yayınlanma tarihi: 18 Haziran 2017; Bağlantı: https://theconversation.com
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel