Hepimiz sosyal medyayı kullanıyoruz. Bu sırada, sık sık kısa ve anlık yanıtlar gerektiren matematik ya da akıl yürütme sorularıyla karşılaşıyoruz. Bu sorular genellikle birkaç sayının sıralandığı ve ardından “Dizideki bir sonraki sayı nedir?” sorusunun geldiği biçimlerde karşımıza çıkar.
Amaç, sayılar arasındaki kuralı yani örüntüyü bulmak ve bir sonraki sayıyı belirlemektir. Birkaç örnek mi istiyorsunuz? Elbette. Aşağıdaki dizilerde bir sonraki sayı nedir?
- 1, 3, 5, 7, 9, 11…
- 1, 4, 9, 16, 25, 36…
- 1, 2, 4, 8, 16…
Şimdi cevaplara geçelim. Tahmin ettiğiniz gibi, ilk dizimiz tek sayılardan oluşuyordu. Bu nedenle, sıradaki sayı 13 olmalıdır. İkinci dizide ise kare sayılar yer alıyordu. Bu durumda, bir sonraki sayı 49 olacaktır. Son dizimiz, 2 sayısının kuvvetlerinden oluşuyor. Dolayısıyla, aradığımız sayı 32 olmalı.
Emin misiniz? Eğer cevabınız “Evet” ise… lütfen kesin emin olmayın. Dizide bir sonraki sayının 32 olacağını düşünmek makuldür, ama yanlıştır.
Genelleme Yapmak Tuzağa Düşmenize Neden Olur
Bir diziyi anlamak için önce terimlerin hangi kuralla üretildiğini bulmaya çalışırız. Ancak ilk birkaç terim bu kuralı kesin olarak belirlemez; bu yüzden tek bir doğru cevap yoktur. Hatta verilen terimlere uyan ve sonraki terimi istediğimiz herhangi bir değer yapacak alternatif bir kural kurmak bile mümkündür.
Şimdi şu soruyu ele alalım: Bir çember üzerindeki N noktasının her birini diğer N−1 noktaya bağladığımızda kaç bölge oluşur? Küçük N değerleri için bölgeleri saymak kolaydır. Elde edeceğimiz sonuç 1, 2, 4, 8, 16 biçiminde olacaktır.
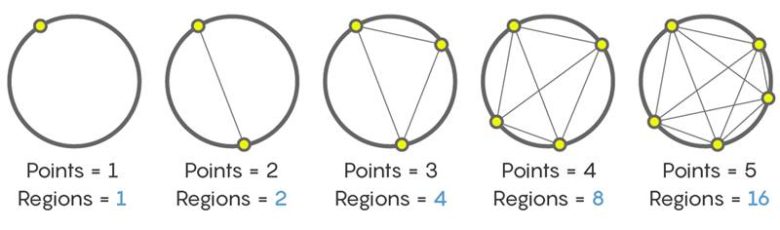
Peki, altı nokta kullanıldığında kaç bölge oluşur? Cevap 32 gibi görünür, ama doğru değildir. Altı nokta çemberi 31 bölgeye ayırır. Çizime bakınca bunu sayarak doğrulayabilirsiniz.
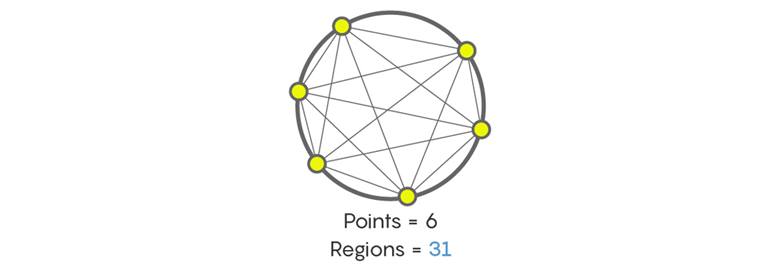
Elbette, 1, 2, 4, 8, 16, 32, 64… gibi, her seferinde ikiye katlanarak artan düzenli örüntüler vardır. Ancak, 1, 2, 4, 8, 16, 31, 57, 99… biçiminde ilerleyen örüntüler de mevcuttur.
Bu nedenle, “Bir sonraki sayı nedir?” diye sorduğumuzda tek bir doğru yanıt beklemek bir yanılgıdır. İşte bu yüzden matematikçiler yalnızca güçlü kanıtlara değil, kesin ispatlara ihtiyaç duyar. Matematiksel gerçeği mümkün kılan şey, ancak ispattır. Bazen tüm işaretler dizideki bir sonraki sayının 32 olduğunu gösterebilir. Ama ispat olmadan bundan emin olamayız.
Genelleme Hatasına Bir Başka Örnek
Verilen birkaç terimi tam olarak karşılayan bir fonksiyon oluşturabiliriz ve bu fonksiyonun devamını istediğimiz gibi ayarlayabiliriz. Bu da dizinin “bir sonraki terimi”nin tek ve zorunlu bir sonuç olmadığını gösterir. Sinc fonksiyonunun tanımına bakalım:
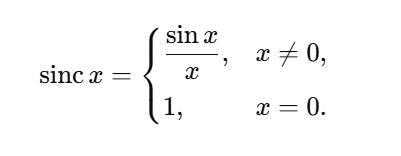
Bu fonksiyon ∣x∣ büyüdükçe küçülen bir salınım yapar ve ±π,±2π,… noktalarında sıfır olur. Bu yüzden sincπ(x−m) ifadesi, x=m olduğunda 1 değerini alır; diğer bütün tam sayılarda 0’a düşer. Bu özellik sayesinde sinc fonksiyonu, “yalnızca bir noktayı seçen bir filtre” gibi davranır. Bu filtreyi kullanarak verilen bir diziyi aynen karşılayan bir fonksiyon tanımlayabiliriz.
Dizi S={a1,a2,…,an} biçiminde olsun. Bu diziyi karşılayan fonksiyon aşağıdaki gibidir ve bu fonksiyon seçeceğimiz keyfi k değerleri için dizinin tüm terimlerini üretir. Doğal olarak, diziyi istediğimiz bir sayı ile genişletirsek, fonksiyon da bu yeni sayıyı doğru şekilde üretir.
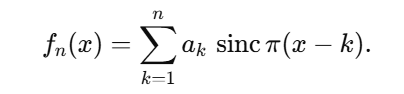
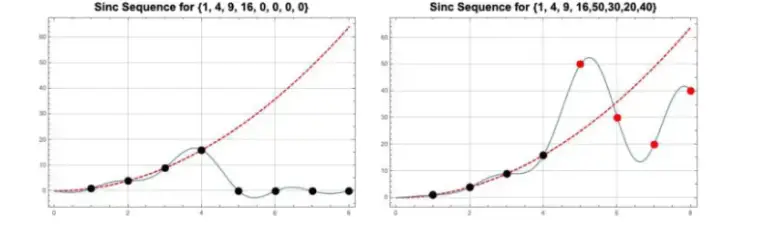
Örneğin 1, 4, 9, 16 dizisini ele alalım. Bu dört noktayı tam olarak karşılayan sinc fonksiyonu soldaki gibi olur. Sonra diziyi tamamen keyfî biçimde genişletelim: 1, 4, 9, 16, 50, 30, 20, 40. Bu kez yeni dizinin sekiz noktasını karşılayan sinc fonksiyonu grafiği de sağdaki grafik biçiminde olacaktır.
Her iki grafikte de şu açıkça görülür: Fonksiyon, verilen tüm değerlere tam olarak uyar; ancak diziye eklediğimiz yeni sayılar fonksiyonun şeklini dramatik biçimde değiştirir. Bu da bir dizinin “doğal devamı”nın tek olmadığını gösterir.
Sonuç Olarak
Bir dizinin ilk birkaç terimi verildiğinde, bu değerlere tam uyan ve sonraki terimleri istediğimiz gibi alabilen çok sayıda fonksiyon tanımlayabiliriz. Bu nedenle mantıksal açıdan “Sıradaki sayı nedir?” sorusunun tek ve kesin bir cevabı yoktur.
Neyse ki matematikçiler bu durumun farkındadır. Bu nedenle içgüdüleri ne kadar ikna edici olursa olsun, arka planda hayal bile edemedikleri bir şey olduğunu bilirler. Bu nedenle de genelde içgüdülerine fazla güvenmezler. Bir sonraki zeka sorusunu çözerken bunların da aklınızda bulunmasını öneririz.
Yazımızın bitiminde ayrıca göz atmak isterseniz: Kolakoski Dizisi: En İlginç Sayı Dizilerden Birisi İle Tanışın
Kaynaklar ve ileri okuma:
- Where Proof, Evidence and Imagination Intersect; Yayınlanma tarihi: 14 Mart 2019; Kaynak site: Quanta Magazine. Bağlantı: Where Proof, Evidence and Imagination Intersect
- What’s the Next Number? yayınlanma tarihi: 24 Kasım 2022; Bağlantı: https://thatsmaths.com/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





