Orta Çağ’da Batı’da meydana gelen entelektüel yavaşlamanın ardından, on yedinci yüzyıl Avrupa’sı, merkez üssü Fransa olan bir matematiksel Rönesans yaşadı. Descartes, bilginin bu yeniden dirilişi sırasında, geleneğin ve otoritenin karşısında aklı, deneyi ve gözlemi tercih ederek, çağının hakim bilimsel düşüncesini sorgulamaya cesaret eden parlak bir filozof olarak ortaya çıktı. Bu dönemde, matematiksel düşüncenin en zengin damarlarından biri olan analitik (veya Kartezyen) geometrinin temelleri de atılacaktı.
Çağdaşları tarafından “Büyük Geometrici” olarak bilinen Pergalı Apollonius (MÖ 262–190), Conics adlı kitabıyla analitik geometrinin gelişimini 1.800 yıldan fazla bir süre önce haber vermişti. Ancak koordinat sisteminin geliştirilmesi İslam ve Hint matematikçileri tarafından cebir olgunlaştıktan sonra olacaktı.
16. yüzyılın sonunda, Fransız matematikçi François Viète bilinen ve bilinmeyen sayısal miktarları temsil etmek için harfleri kullanan ilk sistematik cebirsel gösterimi tanıttı. Cebirsel gösterimin gücüyle, matematikçiler problemleri çözmek için geometrik şekillere ve sezgiye bağımlı olmaktan kurtuldular.

Analitik geometri diğer adıyla koordinat geometrisi, geometri ile cebri birleştiren bir matematik dalıdır. Analitik geometrinin önemi, geometrik eğriler ve cebirsel denklemler arasında bir ilişki kurmasıdır. Bunun sayesinde geometrideki problemleri cebirdeki eşdeğer problemler olarak yeniden formüle edilir. Bu esnada iki Fransız matematikçi René Descartes ve Pierre de Fermat daha cesur davrandı. Descartes ve Fermat, 1630’larda Viète’nin çalışmalarından yola çıkarak analitik geometrinin temellerini birbirinden bağımsız olarak kurdular.

Analitik Geometri Cebir İle Geometri Arasında Bir İlişki Kurdu
Descartes’ın incelemelerinin en ünlüsü olan Yöntem Üzerine Konuşmalar, cebirsel kavramları ilk kez geometrik nesnelerle ilişkilendiren ve analitik veya Kartezyen geometrinin ortaya çıkmasına yol açan Geometri ekini içerir. Kartezyen geometri (Cartesian geometry) ifadesinden “Kartezyen” Cartesius kelimesinden gelir ve Latince Descartes’in ismidir.

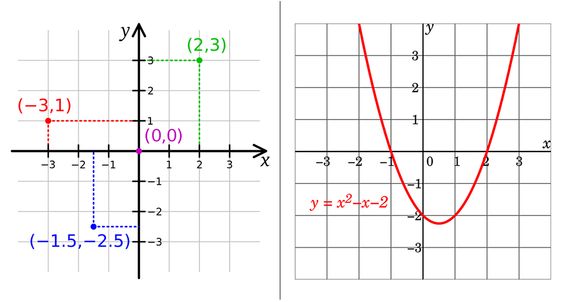
Bu yeni geometride düzlemdeki noktalar (x, y) sıralı ikilileri ile tanımlanır. Bu iki sayı bize koordinat eksenleri adı verilen iki dik çizgiden oluşan sistemde, bir noktanın konumunu verir. Descartes cebir ve geometri arasında bir köprü kurmanın ve sayı çiftlerini noktalarla ilişkilendirmenin yanı sıra, düzlemde çizilen çizgileri iki değişkenli (x ve y) denklemlerle tanımlamasına olanak tanıyan bir tür kılavuz da geliştirmişti.
O ana kadar baskın geometri, problemleri çözmek için cetvel ve pergel kullanan Öklid geometrisiydi. Ancak Descartes’ın yöntemi daha pratikti. Çünkü analitik geometri yardımı ile iki değişkenli bir denklemi bir çizgi ile göstermek mümkün olmuştu. Daire, konikler ve diğer şeyler de farklı dereceden denklemlerin bir sonucuydu.
Pierre de Fermat’ın Analitik Geometriye Katkıları
Fransız matematikçi Pierre de Fermat da analitik geometriye önemli katkılarda bulundu. Fermat, bir eğrinin herhangi bir noktasındaki teğet çizgisini elde etmek için bir yöntem geliştirmişti. Ancak Descartes bunun doğru bir yöntem olmadığına inanıyordu ve bu yüzden Fermat’a meydan okumaya karar verdi. Bu nedenle 1638 yılında aşağıda gördüğünüz eğriyi tanımladı.
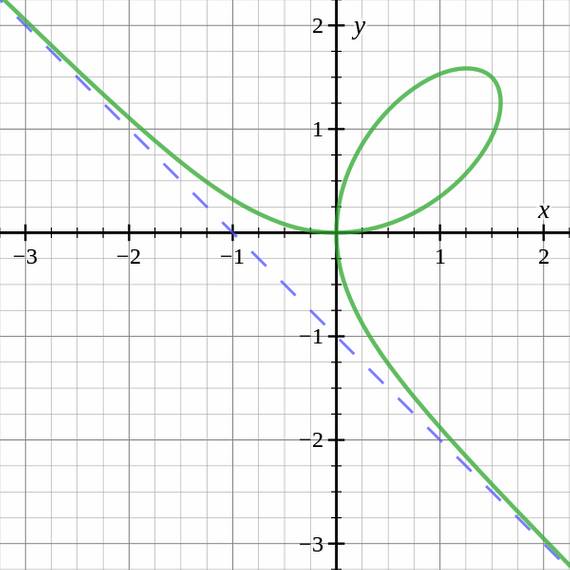
Bu eğri günümüzde Folium of Descartes ( Descartes’ın Folyosu) olarak bilinmektedir. Denklemi x3 + y3 – 3axy = 0 biçimindedir. Fermat bu soruyu da çömüş ve Descartes’a kanıt sağlayarak, geliştirdiği yönteminin başarısını göstermişti. Bu sayede de Newton ve Leibniz sonsuz küçükler hesabının temellerini atabileceklerdi.
Hem Descartes hem de Fermat, uzaydaki eğrileri ve yüzeyleri incelemek için üç koordinat kullanmayı önermelerine rağmen, üç boyutlu analitik geometri, Leonhard Euler, Jakob Hermann ve Alexis Clairaut’un silindirler, koniler için genel denklemler ürettikleri yaklaşık 1730 yılına doğru yavaş yavaş gelişti.

Sonuç olarak
Ancak Descartes, dış dünyaya ilişkin inançlarımız ve kuramlarımızda, matematikte çarpıcı bir biçimde bulduğu kesinliği bulamamıştı. Bu nedenle Meditasyonlar’ın ilk bölümünün çoğunda, doğru olduğunu varsaydığımız her şeyden nasıl ve neden şüphe ettiğini açıklamıştı.
Descartes’in ünlü “düşünüyorum o halde varım” mottosu, bir insan için şüphe edemeyeceği tek varlığın kendisi olduğunu ifade eder. O’nu bu yargıya ulaştıran yolun ilk adımı, dünyadaki neredeyse bütün bilgilerimizin kaynağı olan duyulardan şüphe etmesidir. Kendisi hakkında daha fazla bilgiyi bu yazımızda bulacaksınız. Düşünüyorum Öyleyse Varım Diyen Descartes Aslında Ne Demek İstiyor?
Kaynaklar ve İleri okumalar:
- Descartes and the Rebirth of Geometry. Yayınlanma tarihi: 24 Haziran 2018. Kaynak site: BBVA Open Mind. Bağlantı: Descartes and the Rebirth of Geometry. Erişim Tarihi: 18 Nisan 2024.
- D’Souza, Harry Joseph and Bix, Robert Alan. “analytic geometry”. Encyclopedia Britannica, 6 Jun. 2016, https://www.britannica.com/science/analytic-geometry. Erişim Tarihi: 18 Nisan 2024.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel