Genellikle “istatistikler yalan söyler” deriz; oysa istatistik asla yalan söylemez. Çünkü istatistik, matematikten doğan güçlü ve zarif bir disiplindir. Çevremizdeki karmaşık veriler içinde saklı kalıpları görmemizi sağlar. Fakat mesele bu kalıpları yorumlamaya geldiğinde, sezgilerimiz çoğu zaman bizi yanıltır ve bunun sonucunda çeşitli istatistiksel hatalara düşeriz.

Dikkat Etmeniz Gereken İstatistik Hataları
1. Küçük farkları anlamlı sanmak
Borsadaki günlük dalgalanmaların çoğu, aslında rastlantısal hareketlerden ibarettir ve kayda değer bir anlam taşımaz. Benzer şekilde, anketlerde bir partinin yalnızca bir ya da iki puan önde görünmesi de çoğu zaman istatistiksel gürültüden başka bir şey değildir.
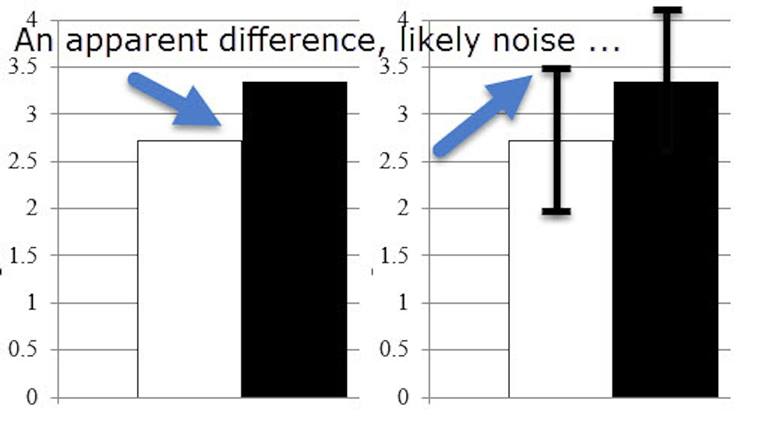
Bu tür dalgalanmaların nedenleri hakkında yanlış çıkarımlara düşmemek için, rakamların “hata payını” görmek gerekir. Eğer fark, hata payından küçükse, büyük olasılıkla ortada gerçek bir fark yoktur; görülen değişim yalnızca rastgele dalgalanmalardan kaynaklanıyordur.
2. İstatistiksel anlamlılığı, gerçek dünya anlamlılığıyla karıştırmak
Çoğu zaman iki grup arasında farklılıklar olduğuna dair genellemeler duyarız. Örneğin, kadınların daha şefkatli, erkeklerin ise daha güçlü olduğu söylenir.

Bu tür iddialar genellikle klişelere ve halk arasında dolaşan bilgilere dayanır, fakat çoğu zaman iki grup arasındaki benzerlikleri ve her grubun kendi içindeki çeşitliliği göz ardı eder. Rastgele seçilen iki erkeğin fiziksel güçleri arasında büyük farklılık olabilir. Yine rastgele seçilen bir erkek ile bir kadın, şefkat konusunda birbirine çok benzer olabilir ya da erkek, kadından daha şefkatli çıkabilir.
Bu istatistik hatasından kaçınmanın yolu, gruplar arasındaki farkların “etki büyüklüğüne” bakmaktır. Etki büyüklüğü, bir grubun ortalamasının diğer grubun ortalamasından ne kadar farklı olduğunu ölçer.
Eğer etki büyüklüğü küçükse, gruplar aslında birbirine oldukça benzer demektir. Etki büyüklüğü büyük olsa bile, grupların kendi içlerinde ciddi farklılıklar bulunur. Bu yüzden bir gruptaki tüm bireyler, diğer grubun tüm bireylerinden farklı olmayacaktır.
3. Veri Kümesinde Aykırı Değer (Uç Değer) Analizi Yapmamak
İncelediğiniz olgu “normal dağılım” (ya da çan eğrisi) gösteriyorsa, etki büyüklüğünün farklı bir yönü devreye girer. Böyle bir dağılımda insanların çoğu ortalama civarında toplanır. Yalnızca çok küçük bir grup ortalamanın çok üzerinde ya da çok altında yer alır.

Bu durumda gruptaki küçük bir performans değişikliği, ortalama birey için neredeyse hiçbir şey ifade etmez. Fakat dağılımın uç noktalarındaki tabloyu ciddi biçimde değiştirecektir. Örneğin, ortalama bir öğrencinin matematik notunu 2 puan artırmak büyük fark yaratmaz. Ama aynı 2 puan, üniversiteye giriş sınavında en üst yüzde 1’lik dilimde yer alan bir öğrenciyi sıralamada yüzlerce basamak ileri taşır.
Dolayısıyla hataya düşmemek için, incelediğiniz farkın ortalamayı mı yoksa uç değerleri mi etkilediğini düşünmek gerekir. Ortalama insanlar söz konusu olduğunda küçük grup farklarının pek önemi yoktur. Ancak mesele uç değerler olduğunda, aynı küçük farkların çok büyük sonuçları olur.
4. Tesadüfi İlişkilere Anlam Atfetmek
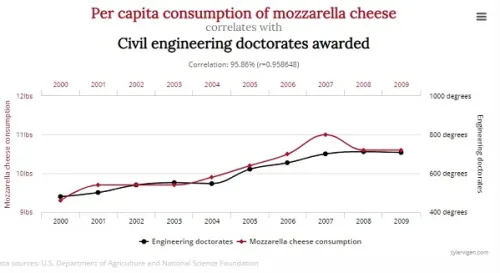
Bir kavşaktan geçen araba sayısı ile bir ağaçtan düşen yaprak sayısı arasında ya da ABD’de kişi başına düşen mozeralla peyniri tüketim miktarı ile doktoralı inşaat mühendisi arasında bir ilişki olduğunu biliyor musunuz? İnanmıyorsanız aşağıdaki grafiğe göz atabilirsiniz.
Aslında yeterince ararsanız bu tür “ilginç” ilişkiler her zaman bulabilirsiniz. Ancak bunların çoğu yalnızca tesadüften ibarettir. İki şeyin aynı anda değişmesi ya da benzer bir desen izlemesi, aralarında gerçek bir bağlantı olduğu anlamına gelmez.
Bu noktada yapılan tipik istatistik hatası, korelasyonu nedensellikle karıştırmaktır. Yani iki şeyin birlikte değişmesini, birinin diğerine neden olduğu şeklinde yorumlamaktır.
Bu hatadan kaçınmak için gözlenen ilişkinin ne kadar güvenilir olduğunu sorgulamak gerekir. Tek seferlik bir durum mu, yoksa defalarca tekrarlanıyor mu? Gelecekte de benzer şekilde öngörülmesi mümkün mü? Eğer yalnızca bir kez karşınıza çıkıyorsa, büyük olasılıkla rastlantıdan başka bir şey değildir.
5. Ters Nedensellik İlişkisi
İki değişken arasında korelasyon gördüğümüzde — örneğin işsizlik ile ruh sağlığı sorunları arasında — çoğu kişi “açık” gibi görünen bir neden-sonuç ilişkisine atlar. Örneğin, ruh sağlığı sorunlarının işsizliğe yol açtığını varsayar.
Oysa nedensellik bazen tam tersi yönde işler: İşsizlik de ruh sağlığını bozar. Hatta iki yönlü bir etkileşim gelişir. Biri diğerini tetiklerken aynı zamanda ondan etkilenir ve bir geri besleme döngüsü oluşur.
Buradaki istatistik hatası, nedenselliğin yönünü yanlış yorumlamaktır. İnsanlar doğru ilişkiyi görür ama yanlış tarafa çevirir. Bu hatadan kaçınmak için bir ilişkiyle karşılaştığınızda ters nedensellik ihtimalini mutlaka düşünün. Etki ters yönde olabilir mi? Yoksa iki değişken birbirini aynı anda mı besliyor? Bu soruları sormak, sağlıklı yorum yapmanın anahtarıdır..
6. Dış Nedenleri Göz Önünde Bulundurmayı Unutmak

İnsanlar çoğu zaman iki şey arasındaki ilişkiyi açıklarken araya giren “üçüncü faktörleri” hesaba katmaz. Oysa çoğu ilişki, aslında her iki değişkeni de etkileyen dış bir nedenden kaynaklanır.
Örneğin, restoranda yemek yemek ile kalp-damar sağlığı arasında bir ilişki bulduğunuzu düşünün. İlk bakışta, restoranda yemek yemenin kalp sağlığını geliştirdiğini sanabilirsiniz.
Fakat gerçekte düzenli olarak restoranda yemek yiyebilen kişiler genellikle daha yüksek sosyoekonomik düzeye sahiptir. Bu insanlar daha iyi sağlık hizmetlerine ulaşır ve asıl farkı yaratan da bu hizmetlerdir. Dolayısıyla ilişkiyi restoranda yemek değil, üçüncü faktör olan sosyoekonomik durum açıklar.
Buradaki istatistik hatası, üçüncü faktör yanılgısıdır. İnsanlar görünen ilişkiye odaklanır ama arka plandaki dış nedeni gözden kaçırır. Bu hatadan kaçınmak için bir korelasyon gördüğünüzde kendinize şu soruyu sorun: “Bu ilişkiyi açıklayan başka bir etken olabilir mi? Gözlediğim her iki sonucu da aynı üçüncü faktör mü yaratıyor?”
7.Grafiklerde ölçek ve eksen yanılgısı
Grafiklerde en çok yanıltıcı durumlar, dikey eksenin ölçeklendirilmesi ve etiketlenmesi sırasında ortaya çıkar. Etiketlerin, incelenen verinin anlamlı olan tüm aralığını göstermesi gerekir.
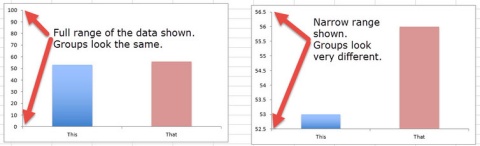
Ama bazı grafik hazırlayanlar bilerek dar bir aralık seçer. Böylece aslında küçük olan fark veya ilişki, olduğundan çok daha büyükmüş gibi görünür. Örneğin, 0’dan 100’e uzanan bir ölçekte iki sütun neredeyse aynı boyda görünür. Fakat aynı veriyi 52,5 ile 56,5 arasını göstererek çizerseniz, sütunlar arasında dramatik bir fark varmış gibi görünür.
Buradaki istatistik hatası, ölçek manipülasyonudur. İnsan gözü küçük oynamaları büyük farklılıklarmış gibi algılar. Bu tuzağa düşmemek için grafikteki eksen etiketlerine mutlaka dikkat edin. Özellikle eksenleri belirtilmeyen grafiklere karşı daha da şüpheci olun.
Sözün özü: İstatistik asla yalan söylemez; ama ona yalan söyletmek için türlü yollar denenir. Gerçekler, acı da olsa bilinmeyi hak eder ve eninde sonunda karşımıza çıkar.
Kaynaklar ve ileri okumalar
Meet The 7 Deadly Sins of Statistical Misinterpretation – And How to Avoid Them. Yayınlanma tarihi: 28 Mart 2027. Kaynak site: Conversation. Bağlantı: The seven deadly sins of statistical misinterpretation, and how to avoid them
Matematiksel






Europe, and in Ancient Russia