Altı yıllık bir aralıktan sonra, amatör bir matematik dedektifi sayesinde, yeni bilinen en büyük asal sayıya sahibiz. Üstelik bu asal sayı öncekinden 16 milyon basamak daha fazla.

Aralık 2017’de, eski bilinen en büyük asal sayı, elektrik mühendisi Jonathan Pace tarafından keşfedilmişti. Yeni keşif ise Luke Durant isimli amatör bir matematikçi tarafından yapıldı. Yeni bilinen en büyük asal sayı 41.024.320 ondalık basamak içeriyor. Bu asal sayı aynı zamanda, 52. Mersenne asal sayısıdır.
Peki ama bu keşif neden önemli? Neden sürekli daha büyük asal sayılar aramaya devam ediliyor? Cevap güvenliğimiz ile ilgili. Çünkü asal sayılar olmadan bankacılık bilgileriniz, online alışverişleriniz tehlikeye girecektir.
Küçük bir sayının çarpanlarına ayrılması kolaydır. Ancak sayı büyüdükçe bu durum zorlaşmaya başlar. Bu nedenle daha büyük asal sayılar daha fazla güvenlik demektir. Kriptografi, bilgiyi kodlama ve kod çözme bilimidir ve RSA gibi algoritmalarının çoğu büyük ölçüde asal sayılara dayanır.
En Büyük Asal Sayıyı Nasıl Buluyoruz?
Carl Sagan’ın aynı adlı romanından uyarlanan Mesaj ( Contact) filminde Dr. Ellie Arroway, radyo teleskoplarıyla gökyüzünü tarayarak akıllı dünya dışı yaşamı arar. Sonunda gezegenler arasındaki bu sinyal asal sayılar biçiminde kendisine gelir. Kendisi uzaylıların asal sayıları kozmik bir “merhaba” olarak kullandıklarına inanması tesadüf değildi.
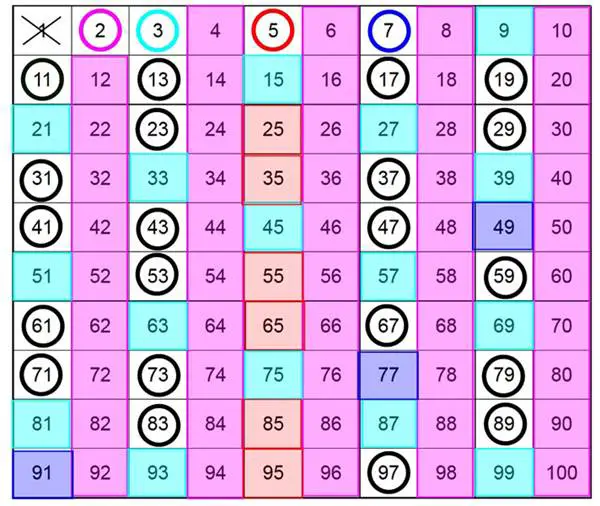
Matematikçiler asal sayıları genellikle matematiğin atomları olarak isimlendirirler. Bunun nedeni tüm sayma sayıların temelinde asal sayıların çarpımı ile oluşturulmasıdır. Mesela 12 sayısını 2x2x3 biçiminde yazabiliriz. Bu sayılara bileşik sayılar denir. Bazı sayıları ise ayırmak mümkün değildir: 2, 3, 5, 7, 11, 13, … Bunlara da asal sayılar veya kısaca asallar denir.
Sonsuz sayıda asal sayı olmasına rağmen hepsini oluşturacak bilinen bir formül yoktur. Bu nedenle çeşitli matematiksel yaklaşımlar ve algoritmalar yardımı ile daha büyük asal sayıları bulma yarışı devam ediyor. Büyük asal sayıları elde etmenin bir yolu, 17. yüzyıl Fransız keşiş, filozof ve matematikçi Marin Mersenne (1588–1648) tarafından keşfedilen bir yöntemden geçiyor.
Mersenne Asalları Nedir?

Günümüzde p doğal sayısı için 2p – 1 şeklindeki sayılara Mersenne sayıları, bunların asal olanlarına da Mersenne asalları denir. Sebebi, Mersenne’in 1644 tarihli Cogitata Physica-Mathematica adlı eserinde 257’ye kadarki tüm p değerlerinden sadece p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 ve 257 değerlerinin bize asal sayı verdiğini iddia etmesidir.
2p – 1 şeklindeki her sayı asal değildir. Örneğin 2⁴ – 1 = 15 sonucu asal olmayacaktır. Eğer 2p – 1 asalsa, p’nin kendisinin de asal olması gerekmektedir. Ancak p asal olsa bile 2p – 1 sayısının asal olduğunun bir garantisi yoktur. Örneğin n=11 asal olmasına rağmen, 2¹¹ – 1 = 2047 sayısı asal değildir çünkü 23 çarpı 89’a eşittir.
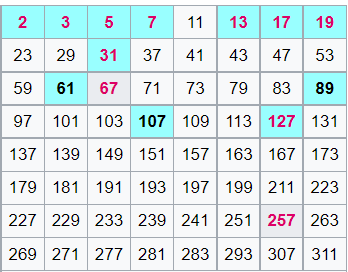
1750 yılında, Leonhard Euler, 231 − 1 sayısının asal olduğunu onayladı. Sonrasında 1876 yılında Fransız matematikçi Édouard Lucas, 2127 − 1 için de onay verdi. Ancak bugün Mersenne’in beş hata yaptığını biliyoruz. İlk olarak p = 67 ve 257 için Mersenne sayıları bileşik sayıdır. Ayrıca listede yer almayan p = 61, 89, 107 gibi üç asal sayı da Mersenne Asalıdır.
1952’de Amerikalı matematikçi Raphael Robinson bu görevi gerçekleştirecek bir bilgisayar programı yazdı. 10 ay içinde sonraki beş Mersenne asal sayısını buldu. Sonraki 50 yıl boyunca, hepsi bilgisayar kullanılarak, hızla yeni Mersenne asal sayıları keşfedildi.
Daha Büyük Mersenne Asalları Bulma Çabası
Great Internet Mersenne Prime Search (GIMPS-Büyük Internet Mersenne Asal Arayışı) aracılığı ile dünyanın dört bir yanından birçok kişi 1996 yılından beri yeni Mersenne asal sayılarını aramaya devam ediyor. 2020’nin sonlarında GIMPS, PRP testi olarak adlandırılan yeni bir teknik kullanmaya başladı. Bu test düşük hata oranı ve kullanım kolaylığı nedeniyle, potansiyel asal sayıları bulmak için gereken hesaplama süresini neredeyse yarıya indirdi.
Bu arada hatırlatalım. İnternet bağlantısı olan iyi bir bilgisayarınız olduğu sürece herkes GIMPS’e dahil olma şansına sahiptir. Mersenne asal sayılarını aramak için ücretsiz yazılım GIMPS web sitesinde yer almaktadır.
Mersenne Asallarının Mükemmel Sayılar İle İlişkisi Nedir?
Mükemmel sayılar hem matematikçileri hem de matematikçi olmayanları tarih boyunca büyülemiştir. Bunun en temel nedeni tanımlanmalarının ve anlaşılmaların kolay olmasından gelir. Günümüzde asal sayılar üretmek için bir formül bulma çalışmasında mükemmel sayılar önemli rol oynar. Ayrıca matematikte çözülemeyen en eski problem yaklaşık iki bin yıllıktır ve size tek mükemmel sayı olup olmadığını sorar.
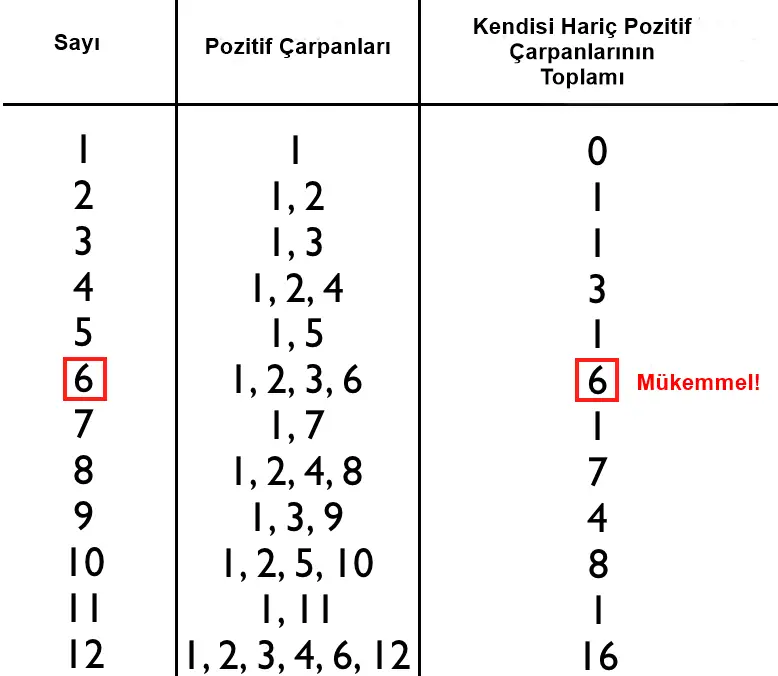
Bir sayının mükemmel olabilmesi için (kendisi hariç) pozitif tam bölenlerinin toplamı bu sayıya eşit olmalıdır. En küçük mükemmel sayı 6’dır. Çünkü bu sayı 6, 2, 3 ve 1’e tam bölünmektedir. Ayrıca 1+2+3=6 toplamına da eşittir. İkinci sırada gelen ise 28 sayısıdır. Bu sayı da 1, 2, 4, 7 ve 14’e bölünür ve 1+2+4+7+14=28’e eşittir.
MÖ 4. yüzyılda Öklid, 2p − 1 asal ise 2p − 1(2p − 1) çarpımının mükemmel bir sayı olduğunu ileri sürmüştü. Örneğin, p=2 ise, formül size 21 × (22 – 1)= 6; p=3 ise 22 × (23 – 1)=28 sonuçlarını verecektir. Öklid mükemmel sayıları bile üretmenin bir yolunu bulmuştu ama bunun tek yol olduğunu kanıtlamadı.
Marin Mersenne mükemmel sayıları kapsamlı bir şekilde incelemişti ve kitabında asal sayılara karşılık geldiğini iddia ettiği bir liste de yayınlamıştı. (p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 ve 257). Bu listedeki ilk 7 sayı ise mükemmel sayıya karşılık geliyor. Mersenne gerçekten mükemmel bir iş çıkarmıştı. Matematikçiler mükemmel sayıları ararken onun bu listesini kullandı.
Sonuç olarak
Bilinen en büyük asal sayı şaşırtıcı derecede büyük olmasına rağmen, onun ötesinde keşfedilmeyi bekleyen sonsuz sayıda asal sayı daha var. Bu keşif, Durant’a GIMPS’ten 3.000$ nakit para kazandırdı. İlk yüz milyon basamaklı asal sayıyı ve ilk milyar basamaklı asal sayıyı keşfedenleri sırasıyla 150.000$ ve 250.000$’lık ek ödüller bekliyor. Ellie Arroway’in Contact’ta yaptığı gibi, tek yapmamız gereken onları aramak.
Kaynaklar ve İleri Okumalar:
- Largest known prime number discovered: Why it matters. Yayınlanma tarihi: 9 Ocak 2018. Kaynak site: Conversation. Bağlantı: Largest known prime number discovered: Why it matters
- Largest known prime number, spanning 41 million digits, discovered by amateur mathematician using free software. Yayınlanma tarihi: 22 Ekim 2024. Kaynak site: Live Sceince. Bağlantı: Largest known prime number, spanning 41 million digits, discovered by amateur mathematician using free software
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






